变量设定误差主要包括相关变量遗漏(也成为模型“欠拟合”)、误选无关变量(也称为模型“过拟合”)两种情况,下面分别探讨这两种情况对估计量及相关检验的影响。
(一)遗漏相关变量偏误
采用遗漏重要解释变量的模型进行估计而带来的偏误称为遗漏相关变量偏误。下面通过一个例子分析遗漏相关变量的影响。
假定真实的模型为
模型(8-1)满足有关线性模型的所有假定。由于种种原因在设定总体回归模型时,将X3遗漏,而将模型误设为
这就意味着实际采用的模型为式(8-2),那么采用普通最小二乘法,由模型(8-2)得到的参数估计量为
其中,n为样本容量,首先对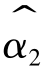 进行分析,由式(8-1)可知,
进行分析,由式(8-1)可知,![]()
![]() ,那么:
,那么:
分别记![]() 。可得
。可得
当样本容量无限大时,可考查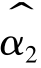 的概率极限性质,对式(8-4)取概率极限可得
的概率极限性质,对式(8-4)取概率极限可得
在不考虑随机解释变量问题的情况下,对式(8-4)两边求期望,可得
对式(8-4)两边求方差可得
由于模型(8-1)完全满足线性回归模型的所有假定要求,所以cov(X2,u)=0,cov(X3,u)=0,
1.如果X2和X3线性相关
由于X2和X3线性相关,所以cov(X2,X3)≠0,这就意味着 ,由于X3是被遗漏的重要变量,所以β3≠0,这就意味着
,由于X3是被遗漏的重要变量,所以β3≠0,这就意味着![]() ,所以在X2和X3线性相关的情况下,
,所以在X2和X3线性相关的情况下, 是β2的有偏且不一致估计量。
是β2的有偏且不一致估计量。
由多重共线性分析中的方差膨胀因子法可知,如果直接采用模型(8-1)进行参数估计,β2的估计量 的方差
的方差 ,其中r2
,其中r2
23为X2和X3线性相关系数,在X2和X3线性相关的情况下,r223≠0,所以![]() ,此时0<r223≤1,势必有
,此时0<r223≤1,势必有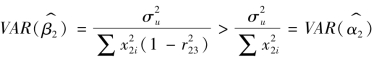 [2]。由此可见,缺失重要变量后,参数估计量的方差变小,从均方差的角度来看,有可能得到一个更精确的估计结果。
[2]。由此可见,缺失重要变量后,参数估计量的方差变小,从均方差的角度来看,有可能得到一个更精确的估计结果。
同理可以证明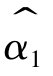 也是
也是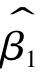 的有偏且不一致估计量。
的有偏且不一致估计量。
对于随机扰动项的方差来讲,对模型(8-1)和模型(8-2)取样本容量为n的样本,
即
Xs=(X1 X2),U= ,那么由模型(8-2)可知:
,那么由模型(8-2)可知:
![]() Xs(Xs′Xs)-1Xs′,易知M是一对称的幂等矩阵。那么:
Xs(Xs′Xs)-1Xs′,易知M是一对称的幂等矩阵。那么:
e=M[(Xs,X3)β+u]=M(Xs,X3)β+Mu
=[I-Xs(Xs′Xs)-1Xs′](Xs,X3)β+Mu
={[I-Xs(Xs′Xs)-1Xs′]Xs,[I-Xs(Xs′Xs)-1Xs′]X3}β+Mu
={0n×2,[I-Xs(Xs′Xs)-1Xs′]X3}β+Mu
=(0n×2,MX3)β+Mu
=(MX3)β3+Mu
那么利用模型(8-2)进行参数估计后的残差的方差与协方差矩阵为
V-COV(e,e)=E(e*e′)=E[(MX3)β3+Mu][(MX3)β3+Mu]′
=E[(MX3)β3β3(X3′M)]+E[(MX3)β3u′M]+E[Muβ3(X3′M)]+E[Muu′M]
=[(MX3)β32(X3′M)]+Mσ2u
由此可得,残差平方和的期望为
E(e′×e)=trace[V-COV(e,e)]=trace[(MX3)β32(X3′M)]+trace(Mσ2u)
其中,
由此可得E(e′×e)=(n-2)(σ2u+β3
2 X3′X3)
从模型(8-2)来看,残差平方和的自由度为n-2,从模型(8-2)得到的随机扰动项的估计量![]() ,易知:
,易知:
除非X3的每一个元素都为零,否则X′3X3>0,可知![]() ,这就导致随机扰动项方差估计量相关的各类检验和参数区间估计容易出现问题。
,这就导致随机扰动项方差估计量相关的各类检验和参数区间估计容易出现问题。
2.如果X2和X3线性不相关
在X2和X3线性不相关的情况下,cos(X2,X3)≠0,这就意味着 ,由式(8-6)可知,
,由式(8-6)可知,![]() ,此时
,此时 是β2的无偏估计量。由式(8-5)易知
是β2的无偏估计量。由式(8-5)易知 是β2的一致估计量。由
是β2的一致估计量。由 可知,当X2和X3线性不相关时,r223=0,那么
可知,当X2和X3线性不相关时,r223=0,那么![]()
![]() ,说明此时
,说明此时 是β2有效估计量。
是β2有效估计量。
由式(8-9)可知:
由X2和X3线性不相关,可知∑x2ix3i=0,u满足高斯-马尔科夫假定则 ,所以
,所以![]() ,除非
,除非![]() ,否则
,否则![]() ,所以一般情况下,
,所以一般情况下, 是β1的有偏估计量。
是β1的有偏估计量。
X2和X3线性不相关,所以cov(X2,X3)=0,u满足高斯-马尔科夫假定,故此cov(X2,u),由此可见,![]() ,除非
,除非![]() ,一般情况下,
,一般情况下, 并不依概率收敛向β1,不满足一致性。
并不依概率收敛向β1,不满足一致性。
(二)包含无关变量的偏误
包含无关变量是指在总体回归函数中包含了不影响被解释变量条件期望的因素,此种情况产生的误差称为包含无关变量偏误。(https://www.xing528.com)
假设正确的模型形式为
而设定的总体回归模型中加入了对被解释变量没有产生系统影响的因素X3,模型误设为
采用OLS对模型(8-13)进行参数估计,可得
由式(8-12)可知:![]() ,将其带入式(8-14)可得
,将其带入式(8-14)可得
即∑x22i=a,∑x23i=b,∑x2ix3i=c,则
由式(8-15)易知![]() ,所以,由模型(8-13)估计出的β1和β2的估计量仍是无偏估计量。
,所以,由模型(8-13)估计出的β1和β2的估计量仍是无偏估计量。
分别对![]() 和
和 求概率极限可得
求概率极限可得
由于模型(8-12)不存在设定误差,因此,cov(X2,u)=0,当cov(X3,u)=0时,![]()
![]() 和
和 满足一致性。
满足一致性。
对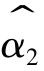 和
和 求方差可得
求方差可得
由此可见:
其中,r223为X2和X3简单线性相关系数的平方。
1.如果X2和X3线性不相关
由式(8-19)和式(8-20)可见,当r223时,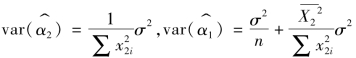
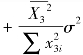 ,与模型(8-12)得出的估计量方差相比,
,与模型(8-12)得出的估计量方差相比,
 仍是β2的有效估计量,但
仍是β2的有效估计量,但![]() 不满足有效性。
不满足有效性。
3.如果X2和X3线性相关
由式(8-14)和式(8-15)可知, 和
和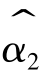 满足线性和无偏性,由高斯-马尔科夫定理可知,在
满足线性和无偏性,由高斯-马尔科夫定理可知,在 和
和 的所有线性无偏性估计量中,估计量的最小方差分别为
的所有线性无偏性估计量中,估计量的最小方差分别为![]()
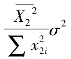 和
和 ,当0<r223≤1时,势必有
,当0<r223≤1时,势必有![]() 和
和![]()
![]() 成立,因此一般情况下,无关变量X3的引入将导致β1和β2估计量方差增大,降低参数估计的精度。同时也导致在β1和β2是否为零的检验中反第二类错误的概率增大。
成立,因此一般情况下,无关变量X3的引入将导致β1和β2估计量方差增大,降低参数估计的精度。同时也导致在β1和β2是否为零的检验中反第二类错误的概率增大。
对模型(8-13)进行参数估计后,得到的残差项向量为
![]() ,记:
,记:
P=I-X(X′X)-1X′,易知,P是一对称的幂等矩阵。那么:
e=PY=P(Xsβ+u)=PXsβ+Pu
那么:
由此可得,残差平方和的期望为
E(e′×e)=trace[V-COV(e,e)]=trace[PXsββ′Xs′P]+trace(Pσ2u)
其中,
trace(Pσ2u)=trace(P)σ2u=trace(I-X(X′X)-1 X′)σ2u
=trace(I)σ2u-trace(X(X′X)-1 X′)σ2u
=nσ2u-trace(X′X(X′X)-1)σ2u
=(n-3)σ2u
trace[PXsXs′P]=β′βtrace[PXsXs′P]=β′βtrace[PXsXs′]
=β′βtrace[XsXs′]-β′βtrace[XsXs′X(X′X)-1 X′]
=β′βtrace[XsXs′]-β′βtrace[XsXs′X′X(X′X)-1]
=β′βtrace[XsXs′]-β′βtrace[XsXs′]
=0
由此可得E(e′×e)=(n-3)σ2u
从模型(8-13)来看,残差平方和的自由度为n-3,从模型(8-13)得到的随机扰动项的估计量![]() ,易知:
,易知:
可见,在过度拟合的情况下,随机扰动项方差的估计量仍是无偏估计量。
(三)遗漏相关变量偏误与包含无关变量偏误的比较
当产生遗漏重要变量偏误时,如果遗漏变量与进入模型的变量之间线性相关,偏回归系数估计量有偏且不一致,但估计量方差会变小;如果遗漏变量与进入模型的变量之间线性不相关,除了截距项外,剩余偏回归系数的估计量仍是线性、无偏、有效、一致估计量,截距项的估计量为有偏、不一致估计量;随机扰动项方差估计量是有偏估计量,且估计量期望大于随机扰动项方差。
当产生包含无关变量偏误时,偏回归系数的估计量是线性无偏一致估计量;如果包含的无关变量与其他变量之间线性不相关,除截距项外,其他偏回归系数的估计量仍是有效估计量;如果包含的无关变量与其他变量之间线性相关,偏回归系数估计量不满足有效性;随机扰动项方差的估计量仍是无偏估计量。
由于在建模之初并不完全清楚隐藏在样本点中的被解释变量与解释变量之间的真实数量关系,这造成在在建模过程中变量选择难以抉择,如果关注无偏性和一致性,包含无关变量优于遗漏重要变量;如果重点关注有效性,遗漏重要变量优于包含无关变量。因此,在一定程度上,模型设定是对偏误和有效权衡后的结果,注重哪一方面取决于研究目的,如果建模的目的是进行预测,最小均方误差则是兼顾有效性和无偏性的良好准则。均方误差(MSE)是参数估计量β*与参数β离差平方的期望:
易知:
MSE(β*)=E(β*-β)2=E[(β*-E(β*))+(E(β*)-β)]2
=E[β*-E(β*)]2+E[E(β*)-β]2+2E[β*-E(β*)][E(β*)-β]
=E[β*-E(β*)]2+E[E(β*)-β]2由此可见,均方误差为估计量β*的方差E[β*-E(β*)]2和估计量均值与参数偏倚的平方的和。当偏倚较小(最小为估计量满足无偏性,此时为零)和有效性(最小方差性)不可兼得需要权衡与折中时,可使用均方误差最小原则进行判断。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




