如何确定自相关系数ρ？

在实际应用中，自相关系数ρ往往是未知的，必须通过一定的方法去估计ρ。最简单的方法是依据DW统计量去估计ρ。由式（6-27）DW与ρ的关系可知

但是，式（6-27）得到的只是一个粗略的结果，这样得到的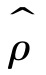只是对ρ精度不高的估计，根本原因在于对有自相关的回归模型使用了普通最小二乘法。为了得到ρ的更精确的估计值，可采用科克伦-奥克特迭代法或德宾两步法

1.科克伦-奥克特（Cochrane-Orcutt）迭代法

科克伦-奥克特迭代法的基本思想是通过逐次迭代去寻求更为满意的ρ的估计值，然后再采用广义差分法，具体来说，该方法是利用残差et去估计未知的ρ。

对于一元线性回归模型Yt=β1+β2Xt+ut，假定ut为一阶自回归形式，即

科克伦-奥克特迭代法估计ρ的步骤如下：

第一步，使用OLS法估计模型Yt=β1+β2 Xt+ut，并计算残差e（1）t：

第二步，利用残差作如下的回归：

第三步，用OLS法估计式（6-29）中的，对模型式（6-21）进行广义差分，即

令，对式（6-30）使用OLS法。可得样本回归函数为

第四步，由前一步估计的结果有和，将代入原回归方程式（6-31），求得新的残差：

第五步，利用残差作回归：

用OLS法估计的是对ρ的第二轮估计值。

当不能确认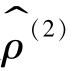是否是ρ的最佳估计值时，继续迭代估计ρ的第三轮估计值，直到估计的与相差很小时，收敛并满足精度要求，或回归所得DW统计量说明已不存在自相关为止。通常，经过迭代很快就能得到有较高精度的，用作广义差分对自相关的修正效果也较好。

续上案例：为解决自相关问题，选用科克伦-奥克特迭代法。由原回归模型：

可得残差序列et，在EViews中，每次回归的残差存放在resid序列中，为了对残差进行回归分析，需生成命名为e的残差序列。在主菜单选择Quick/Generate Series或点击工作文件窗口工具栏中的Procs/Generate Series，在弹出的对话框中输入e=resid，点击OK得到残差序列et。使用et进行滞后一期的自回归，在EViews命今栏中输入ls ee（-1）可得回归方程

et=0.4960 et-1

由式（6-37）可知=0.4960，对原模型进行广义差分，得到广义差分方程

Yt=0.4960Yt-1=β1（1-0.4960）+β2（Xt-0.4960Xt-1）+ut

对上式进行广义差分方程进行回归，在EViews命令栏中输入ls Y-0.4960*Y（-1）c X-0.4960*X（-1），回车后可得方程输出结果如表6-2。

表6-2　广义差分方程输出结果

由表6-2可得回归方程为

式中，(www.xing528.com)

由于使用了广义差分数据，样本容量减少了1个，为18个。查5%显著水平的DW统计表可知dL=1.16，dU=1.39，模型中DW=1.3979＞dU，说明广义差分模型中已无自相关，不必再进行迭代。同时可见，可决系数R2、t、F统计量也均达到理想水平。

对比模型，很明显普通最小二乘法低估了回归系数的标准误差。原模型中=0.0214，广义差分模型中为

经广义差分后样本容量会减少1个，为了保证样本数不减少，可以使用普莱斯-温斯腾变换补充第一个观测值，方法是和。在本例中即为和。由于要补充因差分而损失的第一个观测值，所以在EViews中就不能采用前述方法直接在命令栏输入Y和X的广义差分函数表达式，而是要生成X和Y的差分序列X*和Y*。在主菜单选择Quick/Generate Series或点击工作文件窗口工具栏中的Procs/Generate Series，在弹出的对话框中输入Y*=Y-0.4960*Y（-1），点击OK得到广义差分序列Y*，同样的方法得到广义差分序列X*。此时的X*和Y*都缺少第一个观测值，需计算后补充进去，计算得X1*=345.236，Y1*=275.598，双击工作文件窗口的X*打开序列显示窗口，点击Edit+/-按钮，将X1*=345.236补充到1985年对应的栏目中，得到X*的19个观测值的序列。同样的方法可得到Y*的19个观测值序列。在命令栏中输入Ls Y*c X*得到普莱斯-温斯腾变换的广义差分模型为

对比模型（6.38）和（6.39）可发现，两者的参数估计值和各检验统计量的差别很微小，说明在本例中使用普莱斯-温斯腾变换与直接使用科克伦-奥克特两步法的估计结果无显著差异，这是因为本例中的样本还不算太小。如果实际应用中样本较小，则两者的差异会较大。通常对于小样本，应采用普莱斯-温斯腾变换补充第一个观测值。

由差分方程（6.46）有

由此，我们得到最终的中国农村居民消费模型为

Yt=119.9292+0.5833 Xt

由上式的中国农村居民消费模型可知，中国农村居民的边际消费倾向为0.5833，即中国农民每增加收入1元，将增加消费支出0.5833元。

2.德宾两步法

将广义差分方程式（6-27）表示为

Yt=β1（1-ρ）+β2Xt-ρβ2Xt-1+ρYt-1+υt

采用如下的两个步骤消除自相关。

第一步，将式（6-27）作为一个多元回归模型，使用普通最小二乘法估计其参数。把Yt-1的回归系数看做ρ的一个估计值，它是ρ的一个有偏、一致估计。

第二步，利用估计的进行广义差分。求得序列和，然后使用OLS法对广义差分方程估计参数，求得最佳线性无偏估计量。

本章思考题

1如何使用DW统计量来进行自相关检验？该检验方法的前提条件和局限性有哪些？

2当回归模型中的随机误差项为AR（1）自相关时，为什么仍用OLS法会低估的β^j标准误差？

3判断以下陈述的真伪，并给出合理的解释。

（1）当回归模型随机误差项有自相关时，普通最小二乘估计量是有偏误的和非有效的。

（2）DW检验假定随机误差项ui的方差是同方差。

（3）用一阶差分法消除自相关是假定自相关系数ρ为-1。

（4）当回归模型随机误差项有自相关时，普通最小二乘估计的预测值的方差和标准误差不再是有效的。

4对于四个解释变量的回归模型

Yt=β0+β1 X1t+β2 X2t+β3 X3t+β4 X4t+ut

如果样本量n=50，当DW统计量为以下数值时，请判断模型中的自相关状况。

（1）DW=1.05 （2）DW=1.40 （3）DW=2.50 （4）DW=3.97

5如何判别回归模型中的虚假自相关？

6.在回归模型

Yt=β1+β2Xt+ut

其中，ut无自相关。如果我们错误地判定模型中有一阶自相关，即ut=ρut-1+vt，并使用了广义差分模型

Yt-Yt-1=β1（1-ρ）+β2（Xt-ρXt-1）+vt

将会产生什么问题？