自相关分析：残差图反应的自相关问题

对时间数列进行回归和相关分析，首先遇到的问题是大量的时间数列中存在着受某些因素影响形成的长期趋势，因而在数列前后期的水平之间存在着一定程度的依存关系。例如：某一地区的人口数的变动就受该地区前一时期人口数多少的影响，一个地区社会商品零售额的增长，也受到该地区前期水平多少的影响等。这种按时间先后顺序排列的同一个变量前后期水平之间存在的相关关系，统计中称之为自相关或序列相关。自相关主要是在时间序列分析中提出的概念，在截面数据形成的序列中很少出现。但在研究时间序列时，也因研究目的和数列自身性质的不同而采取不同的步骤和方法。当研究的是由一个变量组成的单一时间数列，研究目的是为了分析其自身的变化规律而不涉及与其他变量的关系，特别是当某一现象的变化难于与其他原因建立联系时，这就需要从变量自身的变化中提取有关未来的信息。例如，关于地震、太阳黑子变动等现象的观测或预报，这就需要用到自回归和自相关，而且在最后对所采用的回归模型是否有还要经过检验，如果误差项存在自相关，也要设法予以消除。另一种情况是研究的对象不是单一的时间数列，而是由双变量或多变量组成的相关时间数列（或以时间t作为解释变量组成的数列）。在这种情况下，要确定的不是单一数列自身的增长趋势，而是和在截面数据中进行回归分析相似，目的是确定解释变量变动与因变量变动之间的依存关系。这时要用到各项回归与相关分析的理论和方法，但不同的是这里的数列是动态的，存在自相关，问题因此变得复杂起来，由此而产生了在时间数列中应用回归分析方法的特殊性，本部分着重讨论的将是这方面的问题。

如影响居民消费的因素很多，但由于受各种条件的限制，通常只引入居民收入一个变量做解释变量，即消费模型设定为

Yt=β1+β2Xt+ut

式中，Yt为农村居民人均消费支出，Xt为农村人均居民纯收入，ut为随机误差项。表6-1是从《中国统计年鉴》收集的中国农村居民1985—2003年的收入与消费数据。

表6-1　1985—2003年农村居民人均收入和消费 单位：元

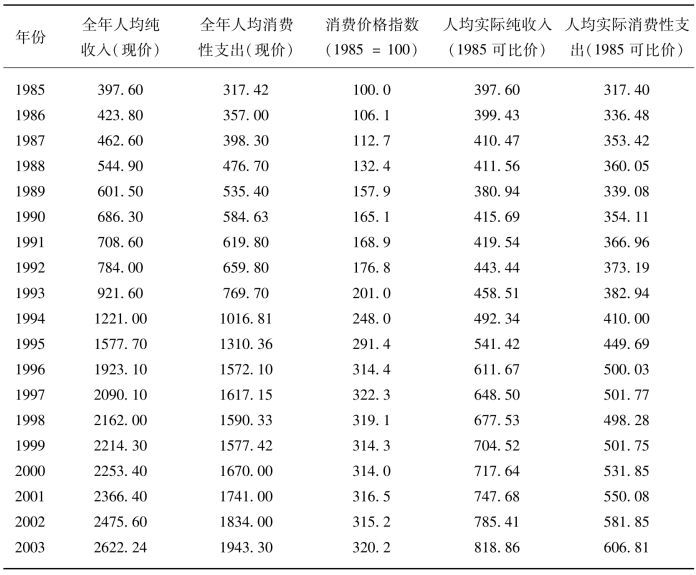
注：资料来源于《中国统计年鉴》1986—2004年。(www.xing528.com)

为了消除价格变动因素对农村居民收入和消费支出的影响，不宜直接采用现价人均纯收入和现价人均消费支出的数据，而需要用经消费价格指数进行调整后的1985年可比价格计的人均纯收入和人均消费支出的数据作回归分析。

根据上表调整后的1985年可比价格计的人均纯收入和人均消费支出的数据，使用普通最小二乘法估计消费模型得

该回归方程可决系数较高，回归系数均显著。对样本量为19、一个解释变量的模型、5%显著水平，查DW统计表可知，dL=1.18，dU=1.40，模型中DW＜dL，显然消费模型中有自相关。这一点残差图中也可从看出，点击EViews方程输出窗口的按钮Resids可得到残差图，如图6-1所示。

图6-1　残差图

在上面残差图中，残差的变动有系统模式，连续为正和连续为负，表明残差项存在一阶正自相关，模型中t统计量和F统计量的结论不可信，需采取补救措施。