如何使用ARCH检验判断时间序列的异方差性？

通常，人们在做计量经济分析时对截面数据产生异方差给予足够的关注，而放松了对时间序列数据产生异方差的警惕。恩格尔（Engel）于1982年提出了在时间序列背景下也有可能出现异方差性，并从理论上提出了一种观测时间序列方差变动的方法，这就是所谓的ARCH（AutoRegressive Conditional Heteroscedasticity）检验方法。ARCH检验的思想是，在时间序列数据中，可认为存在的异方差性为ARCH（自回归条件异方差）过程，并通过检验这一过程是否成立去判断时间序列是否存在异方差。

1.ARCH过程

设ARCH过程为

式中，p为ARCH过程的阶数，并且α0＞0，αi≥0，（i=1，2，…，p）；vt为随机误差。

2.ARCH检验的基本步骤

（1）提出原假设：

H0：α1=α2=…=αp=0； H1：αj（j=1，2，…，p）中至少有一个不为零。(www.xing528.com)

（2）对原模型作OLS估计，求出残差et，并计算残差平方序列，以分别作为对的估计。

（3）作辅助回归

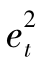式中， 表示的估计。

（4）计算式（5-10）辅助回归的可决系数R2，可以证明在H0成立下，基于大样本，有（n-p）R2渐近服从χ2（p），p为自由度，亦即式（5-9）中变量的滞后期数；给定显著性水平α，查χ2分布表得临界值χα2（p），如果（n-p）R2＞χα2（p），则拒绝原假设，表明模型中的随机误差项存在异方差^[2]。

ARCH检验的特点是，要求变量的观测值为大样本，并且是时间序列数据；它只能判断模型中是否存在异方差，而不能诊断出是哪一个变量引起的异方差。