判断异方差的White检验方法及其应用

White检验的基本思想是，如果存在异方差，其方差与解释变量有关系，分析是否与解释变量的某些形式有联系可判断异方差性。但是 一般是未知的，可用OLS估计的残差平方作为其估计值。在大样本的情况下，作对常数项、解释变量、解释变量的平方及其交叉乘积等所构成辅助回归，利用辅助回归相应的检验统计量，即可判断是否存在异方差性。

例如，二元线性回归模型为

并且，设异方差与X2t，X3t的一般关系为

其中，vt为随机误差项。White检验的基本步骤如下。

1.用OLS法估计式（5-8），计算残差，并求残差的平方。

2.用残差平方作为异方差的估计，并作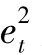对X2t，X3t，X22t，X23t，X2t X3t的辅助回归，即

式中，表示 的估计。(www.xing528.com)

3.计算统计量nR2，其中n为样本容量，R2为辅助回归的可决系数。

4.在H0：α2=…=α6=0，H1：αj（j=2，3，…，6）中至少有一个不为零的原假设下，可证明，nR2渐近地服从自由度为5的χ2分布。给定显著性水平α，查χ2分布表得临界值（5），如果nR2＞（5），则拒绝原假设，表明模型中随机误差存在异方差。

White检验的特点是，不仅能够检验异方差的存在性，同时在多变量的情况下，还能判断出是哪一个变量引起的异方差。此方法不需要异方差的先验信息，但要求观测值为大样本。

续上面案例，由估计结果，按路径view/residual tests/white heteroskedasticity（no cross terms or cross terms），进入White检验。根据White检验中辅助函数的构造，最后一项为变量的交叉乘积项，因为本例为一元函数，故无交叉乘积项，因此应选no cross terms，则辅助函数为

经估计出现White检验结果，见表5.5。

从表5-5可以看出，nR2=18.0694，由White检验知，在α=0.05下，查χ2分布表，得临界值χ20.05（2）=5.9915，比较计算的χ2统计量与临界值，因为nR2=18.0694＞（2），所以拒绝原假设，不拒绝备择假设，表明模型存在异方差。

表5-4