戈德菲尔德-夸特检验：理解与应用

该检验方法是戈德菲尔德和夸特于1965年提出的，可用于检验递增性或递减性异方差。此检验的基本思想是将样本分为两部分，然后分别对两个样本进行回归，并计算比较两个回归的剩余平方和是否有明显差异，以此判断是否存在异方差。

1.检验的前提条件

（1）此检验只适用于大样本（n＞30）（且要求①n≥2（k+1），k是参数的个数）。

（2）除了同方差假定不成立外，其他假定均满足。

检验步骤：若ui具有异方差，其异方差的主要形式之一ui是具有递增的方差。

2.检验的具体做法

（1）将观测值按解释变量Xi的大小顺序排序。

（2）将排列在中间的C个（约1/4）的观察值删除掉，再将剩余的观测值分为两个部分，每部分观察值的个数为（n-c）/2。

（3）提出假设。即H0：两部分数据的方差相等；H1：两部分数据的方差不相等。

（4）构造F统计量。分别对上述两个部分的观察值作回归，由此得到的两个部分的残差平方和，以∑e21i表示前一部分样本回归产生的残差平方和，以∑e22i表示后一部分样本回归产生的残差平方和，它们的自由度均为[（n-c）/2]-k，k为参数的个数。在原假设成立的条件下，因∑e21i和∑e22i分别服从自由度均为[（n-c）/2]-k的χ2分布^[1]，可导出

（5）判断。给定显著性水平α，查F分布表，得临界值 F（α） =。计算统计量F*，如果F*＞F（α），则拒绝原假设，不拒绝备择假设，即认为模型中的随机误差存在异方差。反之，如果F*＜F（α），则不拒绝原假设，认为模型中随机误差项不存在异方差。(www.xing528.com)

戈德菲尔德-夸特检验的功效：一是与对观测值的正确排序有关；二是与删除数据的个数c的大小有关。经验认为，当n=30时，可以取c=4；当n=60时，可以取c=10为宜。该方法得到的只是异方差是否存在的判断，在多个解释变量的情况下，对判断是哪一个变量引起异方差还存在局限。

1.EViews软件操作。

（1）对变量取值排序（按递增或递减）。在Procs菜单里选Sort Series命令，出现排序对话框，如果以递增型排序，选Ascenging，如果以递减型排序，则应选Descending，键入X，点ok。本例选递增型排序，这时变量Y与X将以X按递增型排序。

（2）构造子样本区间，建立回归模型。在本例中，样本容量n=21，删除中间1/4的观测值，即大约5个观测值，余下部分平分得两个样本区间：1—8和14—21，它们的样本个数均是8个，即n1=n2=8。在Sample菜单里，将区间定义为1—8，然后用OLS方法求得表5-2所示结果。

表5-2

在Sample菜单里，将区间定义为14—21，再用OLS方法求得表5-3所示结果。

表5-3

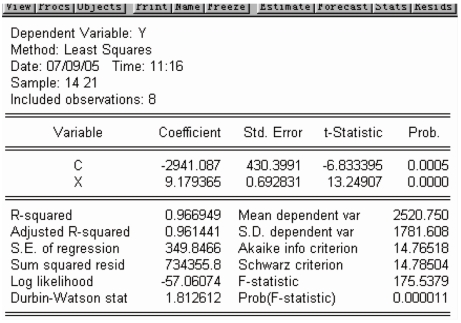
（3）求F统计量值。基于表5-3和表5-4中残差平方和的数据，即Sum squared resid的值。由表5-3计算得到的残差平方和为∑e21i=144958.9，由表5-4计算得到的残差平方和为∑e22i=734355.8，根据Goldfeld-Quanadt检验，F统计量为

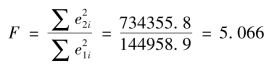
（4）判断。在α=0.05下，式（5.33）中分子、分母的自由度均为6，查F分布表得临界值为F0.05（6，6）=4.28，因为F=5.066＞F0.05（6，6）=4.28，所以拒绝原假设，表明模型确实存在异方差。