消除多重共线性的逐步回归法

依据前述逐步回归的思想，可通过逐步回归筛选并剔除引起多重共线性的变量。其具体步骤如下：（1）用被解释变量对每一个所考虑的解释变量做简单回归；（2）以对被解释变量贡献最大的解释变量所对应的回归方程为基础，按对被解释变量贡献大小的顺序逐个引入其余的解释变量。这个过程会出现3种情形。①若新变量的引入改进了R2和F检验，且回归参数的t检验在统计上也是显著的，则在模型中保留该变量。②若新变量的引入未能明显改进R2和F检验，且对其他回归参数估计值的t检验也未带来什么影响，则认为该变量是多余的，应该舍弃。③若新变量的引入未能明显改进R2和F检验，且显著地影响了其他回归参数估计值的数值或符号，同时本身的回归参数也通不过t检验，则说明出现了严重的多重共线性，应剔除该变量。这种消除多重共线性的方法称为逐步回归法也称Frisch综合分析法。

续第二节案例：采用逐步回归的办法，去检验和解决多重共线性问题。分别作Y对X2、X3、X4、X5、X6的一元回归，如表4-7所示。

首先，我们使用Y对X2，X3，X4，X5和X6分别做一元线性回归模型，结果如表4-7所示。

表4-7　因变量对自变量的逐个回归结果

按R2的大小排序为：X3、X6、X2、X5、X4。

以X3为基础，顺次加入其他变量逐步回归。首先加入X6回归结果为

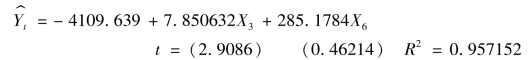
当取α=0.05时，tα/2（n-k）=t0.025（10-3）=2.365，X6参数的t检验不显著，予以剔除，加入X2回归得

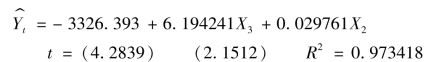
X2参数的t检验不显著，予以剔除，加入X5回归得X3、X5参数的t检验显著，保留X5，再加入X4回归得

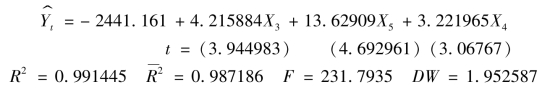
当取α=0.05时，tα/2（n-k）=t0.025（10-4）=2.447，X3、X4、X5系数的t检验都显著，这是最后消除多重共线性的结果。

这说明，在其他因素不变的情况下，当城镇居民人均旅游支出X3和农村居民人均旅游支出X4分别增长1元时，国内旅游收入Yt将分别增长4.21亿元和3.22亿元。在其他因素不变的情况下，作为旅游设施的代表，公路里程X5每增加1万公里时，国内旅游收入Yt将增长13.63亿元。

简答题(www.xing528.com)

1.多重共线性的实质是什么？为什么会出现多重共线性？

2.多重共线性对回归参数的估计有何影响？

3.多重共线性的典型表现是什么？判断是否存在多重共线性的方法有哪些？

4.针对出现多重共线性的不同情形，能采取的补救措施有哪些？

5.在涉及相关的宏观经济总量指标如GDP、货币供应量、物价总水平、国民总收入、就业人数等时间序列的数据中一般都会怀疑有多重共线性，为什么？

6.多重共线性的产生与样本容量的个数n、解释变量的个数k是什么关系？

7.具有严重多重共线性的回归方程能否用来进行预测？

8.以下陈述是否正确？请判断并说明理由。

1）在高度多重共线性的情形中，要评价一个或多个偏回归系数的单个显著性是不可能的。

2）尽管有完全的多重共线性，OLS估计量仍然是BLUE。3）如果有某一辅助回归显示出高的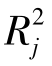值，则高度共线性的存在是肯定无疑的。

4）变量的两两高度相关并不表示高度多重共线性。

5）如果其他条件不变，VIF越高，OLS估计量的方差越大。

6）如果在多元回归中，根据通常的t检验，全部偏回归系数分别都是在统计上不显著的，你就不会得到一个高的R2值。

7）在Y对X2和X3的回归中，假如X3的值很少变化，这就会使Var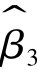（）增大，在极端的情形下，如果全部X3值都相同，Var（）将无穷大。

8）如果分析的目的仅仅是预测，则多重共线性是无害的。