修正多重共线性的实用方法

1.剔除变量法

保留重要的解释变量，去掉次要的或可替代的解释变量；这是最简单的一种方法。当回归方程中存在严重的多重共线性，可以删除引起多重共线性的不重要的解释变量。有几个变量方差扩大因子大于10时，可试探把方差扩大因子最大者所对应的解释变量首先剔除，再重新建立回归方程。如果仍然存在严重的多重共线性，则再继续剔除方差扩大因子最大者所对应的解释变量，直至回归方程中不再存在严重的多重共线性。

2.增大样本容量

由于多重共线性是一个样本特性，所以可能在同样变量的另一样本中共线性又没有那样严重。这时，如果可能，可以通过增大样本容量来减轻共线性的问题。建立一个实际经济问题的回归模型，如果所收集的样本数据太少，是容易产生多重共线性的，从前面式（4-18）和式（4-19）可知，如果样本容量增加，则也会增加，结果会减小回归参数的方差，标准误差也同样会减小。因此尽可能地收集足够多的数据可以改进模型参数的估计。所以在运用回归分析研究经济问题时，要尽量使样本容量远大于解释变量的个数。

3.变换模型形式

将原设定的模型的形式做适当的变换，有可能消除或减弱原模型中解释变量之间的相关关系。对原设定的模型进行适当的变换，也可以消除或削弱原模型中解释变量之间的相关关系。具体有三种变换方式：一是变换模型的函数形式；二是变换模型的变量形式；三是改变变量的统计指标。例如，可采用差分法，这是指将原模型变形为差分模型形式进而减低多重共线性的一个方法。

例4.1 根据表4-4，建立我国进口需求与GNP和消费价格指数之间的关系模型。

表4-4　我国进口支出与GNP和消费价格指数 （单位：亿元人民币）

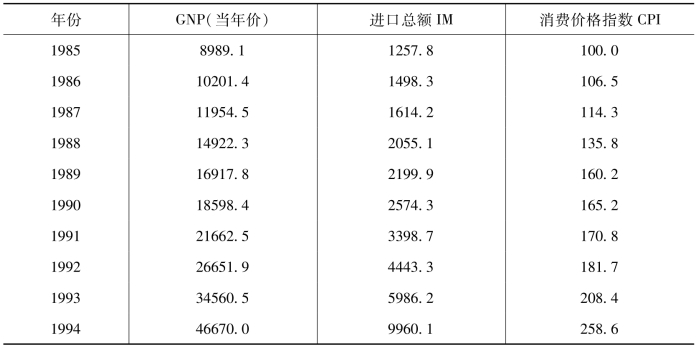
续表

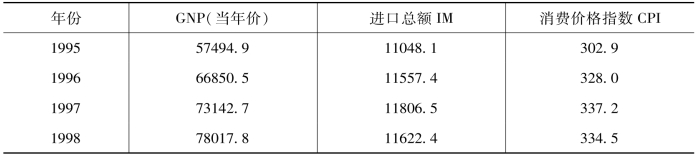
根据表4-4中的数据，回归结果如表4-5所示。

表4-5　进口总额对GNP和CPI的回归结果

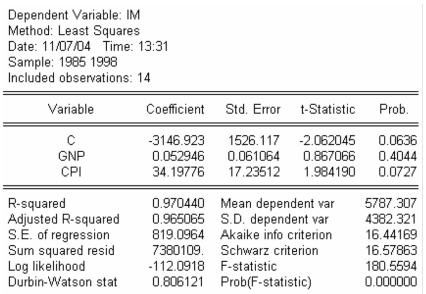
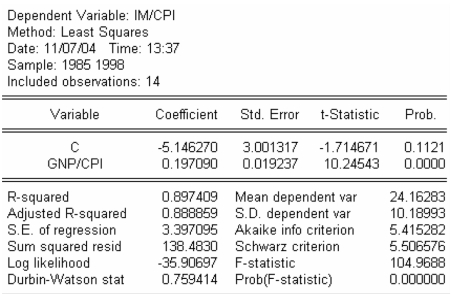
回归结果表明，在5%的显著性水平下，收入和价格的系数各自均不是统计显著的。模型通过F检验。我们可以断定方程中存在严重的多重共线性。为解决这个问题，我们可以用实际进口额对实际收入进行回归，得到如表4-6所示结果。

表4-6　实际进口额对实际收入的回归结果

(www.xing528.com)

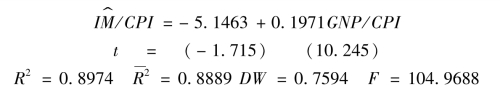
这表明，实际进口额与实际收入显著正相关。这样，通过将名义变量转换为实际变量，显然削弱了原模型中的多重共线性。

4.利用非样本先验信息

如果通过经济理论分析能够得到某些参数之间的线性关系，可以将这种线性关系作为约束条件，将此约束条件和样本信息结合起来进行约束最小二乘估计。

根据经济理论或其他信息，找出参数间的某种关系，并将这种关系作为约束条件与样本信息结合起来，进行有约束的最小二乘估计。例如，著名的Cobb-Douglas生产函数中：

Y=ALαKβ

劳动投入量L与资金投入量K之间通常是高度相关的，如果已知附加信息：α+β=1（即规模报酬不变），则有，或者：，记，则C-D生产函数可以表示成：

y=Akβ

此时二元模型转化成一元模型，当然不存在多重共线性的问题，可以利用OLS法估计A，β进而得到

5.横截面数据与时间序列数据并用

这是先验信息法的一个变种，将横截面数据与时间序列数据组合，称为数据并用（pooling the data）。其基本做法是：首先利用横截面数据估计出部分参数，再利用时序数据估计出另外的部分参数，最后得到整个方程参数的估计。在模型的参数估计中，如果模型利用的是时间序列数据，这时模型又存在多重共线性，可考虑用时间序列数据与截面数据相结合的办法来修正多重共线性对模型的影响。

6.变量变换

有时通过对模型中变量进行变换能够实现降低共线性的目的。例如，常用的变量变换方式有以下几种。

（1）计算相对指标。如原来的是总量指标，可计算人均指标或结构相对数（比重）指标等。经过这样处理的数据有时可以降低共线性。

（2）将名义数据转换为实际数据。将名义数据剔除价格影响后反映的信息在统计上常常是指纯的物量的变化，不包含价格变动的影响，有助于描述现象之间真实的数量变化关系。因此在多数经济分析中采用“实际”数据而不是名义数据，有时名义数据转换为实际数据后可降低多重共线性。

（3）将小类指标合并成大类指标。如例4.1中，工业增加值、建筑业增加值之间呈现高度线性相关，可将其合并成第二产业增加值。这一合并有助于消除多重共线性。

需要指出，变量数据的变换只是有时可得到较好的结果，但谁也无法保证一定可以得到很好的结果。