完全多重共线性对模型的影响

1.参数的估计值不确定

多元线性回归模型

Y=XB+U

的普通最小二乘估计量为

如果解释变量之间存在完全多重共线性，由于X矩阵的系数行列式，逆矩阵（X′X）-1不存在，无法得到参数估计式。

例如，对于二元线性回归模型：

如果两个解释变量完全相关，如x2=λx1，该二元线性回归模型退化为一元线性回归模型

y=b0+（b1+λb2）x1+u

这时，只能确定综合参数b1+λb2的估计值，却无法确定b1，b2各自的估计值。

完全共线性时，X矩阵的秩小于k，此时，正规方程组的解不唯一，（X′X）-1不存在，回归参数的最小二乘估计表达式不成立。(www.xing528.com)

这里以两个解释变量的回归模型Yi=β1+β2X2i+β3X3i+ui为例，说明完全多重共线性的影响。采用离差形式表示的两个解释变量的回归模型为

多元回归的偏回归系数的最小二乘估计量：

假定X2i=λX3i，这里λ是一非零常数，将其分别带入式（4-5）和式（4-6），可得

式（4-7）和式（4-8）都是不定式，这说明当X2i=λX3i时，参数的估计值是不确定的。从回归模型的建模思想看，在回归模型中回归系数的含义是指在保持X3不变的情况下，当X2每变动一个单位时Y的平均变化；回归系数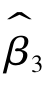的含义是指在保持X2不变的情况下，当X3每改变一个单位时Y的平均变化。如果X2与X3完全共线性，就没有办法能在保持X2不变的情况下，分析X3对Y的影响。或者说，没有办法能从所给的样本中把X2和X3各自的影响分解开来。

2.增大参数估计值的方差

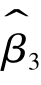还是以只有两个解释变量的回归模型Yi=β1+β2X2i+β3X3i+ui为例，参考多元回归的偏回归系数的最小二乘估计量，已知OLS估计参数的方差为（X′X）-1，容易导出这时参数估计式和的方差为

在完全共线性情况下X2i=λX3i，代入（4-9）和（4.10）式中得

同理

这表明，在解释变量之间存在完全的共线性时，参数估计值的方差将变成无穷大。