总体回归方程显著性检验：方法与结果

偏回归系数的显著性检验用来判断一个偏回归系数是否显著不为零，可决系数主要解释样本回归函数对样本点的解释能力，那么在多元线性回归模型中被解释变量的条件均值与多个解释变量之间的线性关系是否显著，仍需进一步判断。总体回归方程显著性检验就是判断解释变量之间是否存在一个线性组合能够显著的解释被解释变量条件均值的变化。具体步骤如下：

1.提出假设 H0：β2=…=βk=0 H1：β2、…、βk不全为零

当原假设成立时，总体回归函数为E（Yi）=β1（i=1，2，…，n），解释变量的线性组合没有对被解释变量条件均值的变化做出任何解释；当备择假设成立时，至少还有一个解释变量的变化能够对被解释变量条件均值的变化产生显著影响。

2.构建检验统计量

当原假设成立时，总体回归模型为Yi=β1+ui，（i=1，2，…，n），经典假设成立时，Yi（i=1，2，…，n）可视为从一个N（β1，σ2）总体中抽取出的样本容量为n的样本，依据抽样分布的相关定理，可知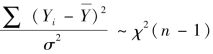。由一元线性回归模型的相关理论可知，总离差平方和可以分解为回归平方和与残差平方和两部分，，由于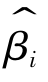都与Qe相互独立，故此与Qe相互独立，那么，∑的自由度等于的自由度与Qe自由度之和，而的自由度为n-1，Qe的自由度为n-k，所以的自由度为k-1。

将总离差平方和分解公式两边同除以σ2可得

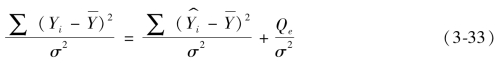
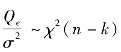，当原假设成立时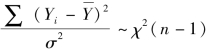，，依据克赫伦分解定理，当原假设成立时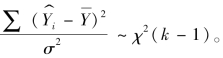，(www.xing528.com)

由与Qe相互独立，可知：

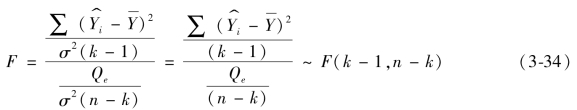
3.利用样本点信息计算检验统计量观测值F0。

4.计算检验P值。

由于ei是对随机扰动项ui一次观测值的估计，因此Qe中只含有偶然性因素；当原假设成立时，E（Yi）=β1，（i=1，2，…，n），因此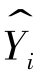，之间的差异仅为抽样带来的偶然性波动，亦即也仅含抽样的偶然性；这就意味着当原假设成立时，式（3-34）的分子和分母主要是由偶然性因素决定的，二者之间不应存在显著差异。当备择假设成立时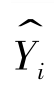，之间的差异除了抽样的随机性带来的偶然因素之外，还包含解释变量变化带来的E（Yi），（i=1，2，…，n）之间的系统性波动，因此，当备择假设成立时，式（3-34）的分子中不仅包含偶然性波动，还包含系统性波动，此时分子应显著大于分母，因此，此检验为右侧检验，P值定义为

5.检验决策。将P值与提前给定的显著性水平α进行比较，如果P＞α则没有理由拒绝原假设，在实际决策中认为在给定的显著性水平α下总体回归方程整体不显著，反之，如果P＜α，则不接受原假设，在实际决策中认为在给定的显著性水平α下总体回归方程是显著的。

表3-2中的F-statistic对应的是F0，Prob（F-statistic）为对应的P值，如果设定显著性水平α=0.05，易知P＜α，这说明总体回归模型（3-18）对应的总体回归方程Yi=β1+β2X2i+β3X3i总体是显著的。