拟合优度检验方法与多元线性回归模型

与一元线性回归模型中利用可决系数表征样本回归函数对样本点的拟合程度一样，在多元回归模型中同样也需要样本回归函数对样本点的解释能力。

1.多重可决系数

与一元线性回归模型中可决系数的定义一样，在多元线性回归模型中多重可决系数仍定义为

由于样本回归函数依然过均值点，那么：，那么：

，（i=1，2，…，n），因此：

在给定的样本点中，由于的符号决定了Xj与Y简单线性相关系数的符号，而Xj与Y简单线性相关系数的符号往往与相同，由此可见，多重可决系数R2一般为解释变量个数的不减函数。

如果为了追求较大的多重可决系数取值而向总体回归方程中加入过多的解释变量，亦即k增大，在保持样本容量n不变的情况下，就会使模型整体自由度n-k下降，就会使得检验和估计的功效下降。以参数的显著性检验为例，当n-k下降时，的方差增大，检验功效就会降低。因此，在进行多元线性回归模型的拟合优度测度时，需要在解释变量个数k和模型的解释能力之间进行权衡，对多重可决系数进行修正。(https://www.xing528.com)

2.修正的可决系数

增加解释变量时，总离差平方和保持不变，因此，可决系数修正主要是通过自由度修正残差平方和和回归平方和，由于n-k是残差平方和的自由度，所以可决系数的修正一般通过修正残差平方和来调节样本回归方程对样本点的解释能力与自由度n-k之间的矛盾；修正的可决系数定义如下：

修正的可决系数与多重可决系数之间存在如下关系：

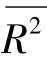由式（3-32）可见，当k=1时，；当k＞1时，由于可知，因此，当k＞1时，，即，此时必有。由，可得，可知当时，由于修正的可决系数主要用来测度样本回归函数对样本点的解释能力，因此，当 ＜0时，规定 =0。

表3-2中的R-squared和Adjusted R-squared分别对应多重可决系数和修正的可决系数，可见 ＜R2。

在处理实际问题的过程中，希望R2和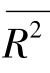越大越好，但多重可决系数和修正的可决系数仅仅是从整体上衡量解释变量某一线性组合对样本点的解释能力，并没有考量偏回归系数的显著性；参数显著性检验虽然评估了单个偏回归系数的可靠性，但是缺乏对偏回归系数整体可靠性的评价。