最小二乘估计量抽样分布及扰动项方差的估计量

1.最小二乘估计量的抽样分布

由于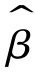满足线性，因此，当正态性假定成立时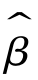，的每个元素均为正态分布，由无偏性可知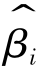的 期望为βi，由，可知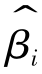，的 方差为矩阵（X′X）-1σ2主对角线上的第i个元素，记（X′X）-1=（lij）k×k，则，因此：

2.随机扰动项方差σ2的估计量及抽样分布

由，记：

A=I-X（X′X）-1X′，

容易证明P为一幂等矩阵，那么：

因此

由此可知 E（e′e）=trace（Aσ2）=trace（A）σ2

trace（P）=trace（I-X（X′X）-1X′）

=n-trace（X（X′X）-1X′）

=n-trace（X′X（X′X）-1）

=n-k

因此，E（e′e）=（n-k）σ2

由此可知(www.xing528.com)

容易证明：β′X′A=β′X′-β′X′X（X′X）-1X′=β′X′-β′X′=0，故此：

A′Xβ=AXβ=0

因此

β′X′AY=0；Y′AXβ=0；β′X′AXβ=0

由此可知

（Y-Xβ）′A（Y-Xβ）=Y′AY-β′X′AY-Y′AXβ+β′X′AXβ=Y′AY

由于e=AY，那么：Qe=e′e=Y′AAY=Y′AY，于是可知：

由于矩阵A的秩为n-k，因此，存在一正交矩阵H，使得D=Hn×n′An×n Hn×n为对角线矩阵，记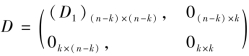，其中D1为（n-k）×（n-k）的单位矩阵；故此：

3.，也就是

在正态性假定成立的情况下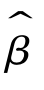，与e的各分量都是正态分布，由于0，所以，任意一个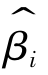都 与Qe相互独立。

4.

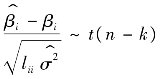
由与Qe相互独立，那么：