(一)参数估计量的评价标准
由参数估计的表达式可知,参数估计值是样本点的函数,这就意味着参数估计值会随着样本点的变化发生变化,存在“抽样波动”,由概率抽样的基本原理可知,一次抽样抽取到样本空间中的某一个样本点是有一定概率的,因此,通过普通最小二乘法和极大似然法得出的参数估计表达式是一个随机变量。进一步推广,将这些表达式视为定义在样本空间上的函数,在样本容量n已经确定的前提下,函数本身不含未知参数,因此,这些参数估计表达式本质上就是对应参数的估计量,在给定样本点的情况下,带入参数估计量的表达式,就可以得到对应参数的点估计值。参数估计中“尽可能接近总体参数”原则的实现主要依赖估计量的性质,计量经济学在探讨“尽可能接近总体参数”原则是否实现时,一般不研究一次点估计的结果,而是通过设定估计量的评价标准,以保障该原则的实现。经常考虑的标准有无偏性、有效性、一致性等。
1.无偏性
对于未知参数βi通过某种准则找到其估计量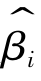 , 如果估计量的期望就是参数本身,即
, 如果估计量的期望就是参数本身,即![]() ,则称此估计量为无偏估计量。假设存在βi的一个有偏估计量
,则称此估计量为无偏估计量。假设存在βi的一个有偏估计量![]() a,(a≠0);假设两个估计量方差相等,密度函数分别记为
a,(a≠0);假设两个估计量方差相等,密度函数分别记为![]() 和
和![]() ,以βi为中点,构建一个半径为ε的区间:(βi-ε,βi+ε),由图2-9易知,无偏估计量在该区域内取值的概率大于有偏估计量在该区域取值的概率;这就意味着如果两个估计量分布形态相同,仅均值不同,无偏估计量估计结果更容易“接近总体参数”。
,以βi为中点,构建一个半径为ε的区间:(βi-ε,βi+ε),由图2-9易知,无偏估计量在该区域内取值的概率大于有偏估计量在该区域取值的概率;这就意味着如果两个估计量分布形态相同,仅均值不同,无偏估计量估计结果更容易“接近总体参数”。
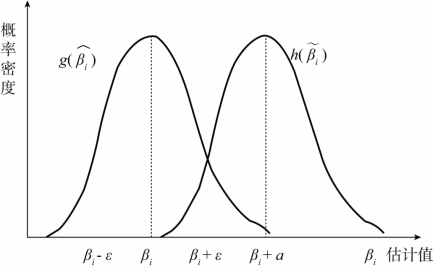
图2-9 无偏估计量与有偏估计量密度函数示意图
2.有效性
对于未知参数βi的估计量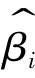 ,如果
,如果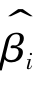 是 βi所有无偏估计量中方差最小的估计量,则称
是 βi所有无偏估计量中方差最小的估计量,则称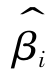 满足就有效性。假定另有一βi的无偏估计量
满足就有效性。假定另有一βi的无偏估计量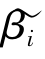 ,但
,但![]() ,密度函数分别记为
,密度函数分别记为![]() 和
和![]() ,同样以βi为中点,构建一个半径为ε的区间:(βi-ε,βi+ε),由图2-10容易看出,对
,同样以βi为中点,构建一个半径为ε的区间:(βi-ε,βi+ε),由图2-10容易看出,对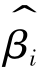 观测一次得到的βi的点估计值落进(βi-ε,βi+ε)的概率大于利用
观测一次得到的βi的点估计值落进(βi-ε,βi+ε)的概率大于利用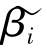 对βi进行一次点估计值落入该区间的概率。因此,对于分布形态相同的两个无偏估计量,利用方差较小的估计量进行参数估计更容易“接近总体参数”。
对βi进行一次点估计值落入该区间的概率。因此,对于分布形态相同的两个无偏估计量,利用方差较小的估计量进行参数估计更容易“接近总体参数”。
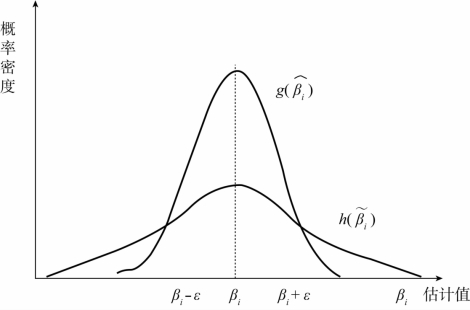
图2-10 有效估计量与无效估计量密度函数示意图
3.一致性(如图2-11所示)
在小样本情况下,有时难以找到有效估计量,这时就需要考虑大样本情况下估计量的渐进性质。对于未知参数βi,如果估计量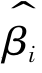 以 概率收敛向βi,则称
以 概率收敛向βi,则称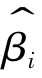 满足一致性。亦即,任取ε>0,当
满足一致性。亦即,任取ε>0,当
![]()
成立时,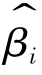 满足一致性。由式(2-33)不难发现,当
满足一致性。由式(2-33)不难发现,当![]() 的一次观测值(也就是βi的一次点估计值)落进(βi-ε,βi+ε)的概率极限为1,这就意味着只要样本容量n足够大,满足一致性的估计量
的一次观测值(也就是βi的一次点估计值)落进(βi-ε,βi+ε)的概率极限为1,这就意味着只要样本容量n足够大,满足一致性的估计量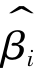 可以以较高的概率落进以βi为中点的任意短的区间(如图2-11所示),这就为参数估计实现“尽可能接近总体参数”原则的实现提供了保证。
可以以较高的概率落进以βi为中点的任意短的区间(如图2-11所示),这就为参数估计实现“尽可能接近总体参数”原则的实现提供了保证。
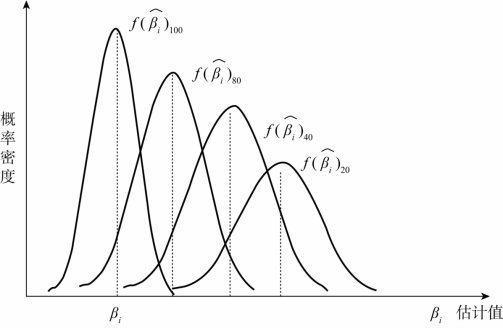
图2-11 估计量满足一致性时估计量密度函数随样本容量增加变化示意图
(二)最小二乘估计量的性质
可以证明在古典假定成立的条件下,线性总体回归模型的估计量具有线性、无偏性和有效性。
1.线性
对于一元线性回归模型的最小二乘估计量,可以证明:
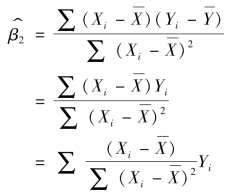
记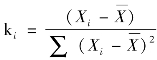 ,易知:
,易知: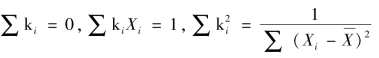
那么
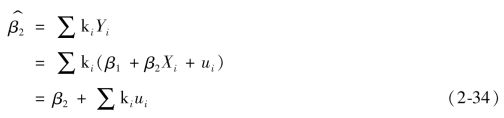
同时可以证明:
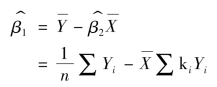
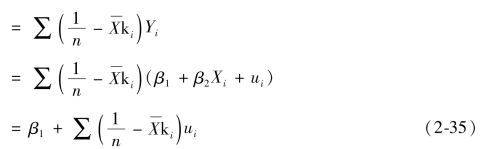
由模型假设可知,解释变量X为非随机变量,其取值为提前设定好的条件,可见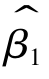 和
和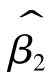 不仅是Yi(i=1,…,n)的线性函数,同时也是随机扰动项ui(i=1,…,n)的线性函数。
不仅是Yi(i=1,…,n)的线性函数,同时也是随机扰动项ui(i=1,…,n)的线性函数。
2.无偏性
当随机扰动项的零均值假定E(u/Xi)=E(ui)=0成立时,由式(2-34)可知:
![]()
同理,利用式(2-35)可证:
![]()
这说明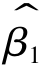 和
和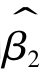 是总体参数β1和β2的无偏估计量。
是总体参数β1和β2的无偏估计量。
3.有效性(https://www.xing528.com)
由式(2-34)和式(2-35)容易证明:
![]() ,如果随机扰动项无自相关假定成立,则可得
,如果随机扰动项无自相关假定成立,则可得![]() ,如果随机扰动项同方差假定成立,则
,如果随机扰动项同方差假定成立,则
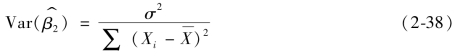
类似可证,如果随机扰动项无自相关和同方差假定成立,
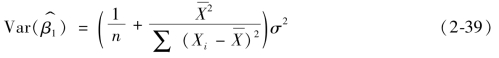
下面以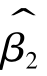 为例,证明最小二乘估计量满足有效性。
为例,证明最小二乘估计量满足有效性。
假设存在β2的另一个线性无偏估计量β*2=∑ωiYi=∑ωi(β1+β2Xi+ui),可知:∑ωi=0,∑ωi Xi=1,当古典假设依然成立时,Var(β*2)=∑ωi2σ2,∑ωi2可以进行如下分解:∑ωi2=∑(ωi-ki+ki)2=∑(ωi-ki)2+∑(ki)2+2∑(ωi-ki)ki,由于
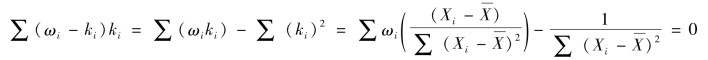
所以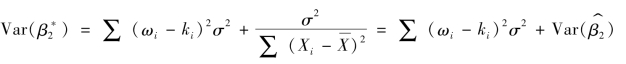
由于∑(ωi-ki)2≥0
因此,![]()
∑(ωi-ki)2=0的充要条件是ωi=ki(i=1,…,n),因此,当∑(ωi-ki)2=0时,β*2即为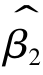 。由此可见
。由此可见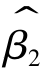 是β2所有线性无偏估计量中方差最小的估计量。
是β2所有线性无偏估计量中方差最小的估计量。
可见,在古典假定成立的条件下,最小二乘估计量是参数估计量的线性、无偏、有效估计量,也称为最佳线性无偏估计量,这一结论即为高斯-马尔科夫定理。
4.估计量的其他性质
随机扰动项方差的极大似然估计量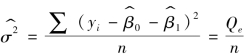 并非σ2的无偏估计量。首先对残差平方和进行变形,可得
并非σ2的无偏估计量。首先对残差平方和进行变形,可得
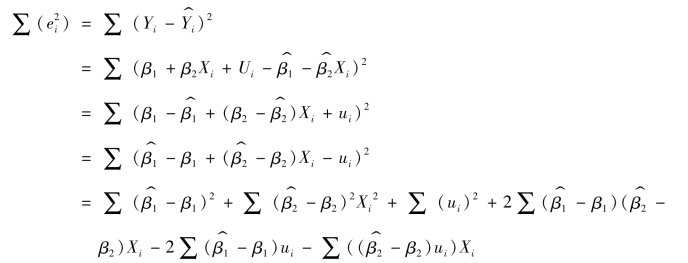
将![]() 带入上式,在同方差假定和无自相关假定成立的条件下,可以证明:E∑(e2i)=(n-2)δ2,因此,δ2的无偏估计量为
带入上式,在同方差假定和无自相关假定成立的条件下,可以证明:E∑(e2i)=(n-2)δ2,因此,δ2的无偏估计量为
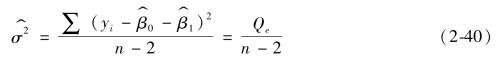
由式(2-34)和式(2-35),结合同方差假定和无自相关假定,可得
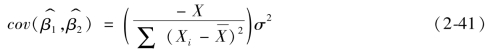
当正态性假定成立时,由最小二乘估计量的线性特性可知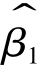 和
和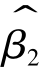 均服从正态分布,结合式(2-36)、式(2-37)、式(2-38)、式(2-39),可知
均服从正态分布,结合式(2-36)、式(2-37)、式(2-38)、式(2-39),可知
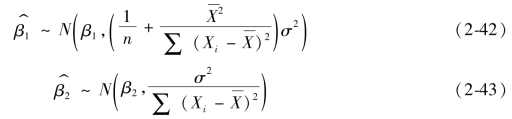
(三)最小二乘估计方法下样本回归函数的性质
1.残差项的和为零,即∑ei=0;Y1…Yn的均值![]() 的均值相等;样本回归线通过样本均值点。
的均值相等;样本回归线通过样本均值点。
与由式(2-22)可知:![]() ,亦即
,亦即![]() ,由此可知∑ei=0,同时可知
,由此可知∑ei=0,同时可知![]() 因此
因此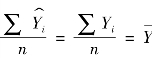 。由
。由![]() 可得
可得![]() ,两边同除以n可得
,两边同除以n可得![]() ,因此,样本回归线过点
,因此,样本回归线过点![]()
![]()
2.残差项与解释变量正交。
由式(2-23)可得![]() ,亦即∑Xiei=0,因此残差项(e1…en)与解释变量(X1…Xn)正交。而
,亦即∑Xiei=0,因此残差项(e1…en)与解释变量(X1…Xn)正交。而![]() 为残差项和解释变量的样本协方差,
为残差项和解释变量的样本协方差,![]() ,而在任意样本点下∑Xiei=0,因此,Cov(X,e)=0,这就意味着解释变量与残差项线性无关。
,而在任意样本点下∑Xiei=0,因此,Cov(X,e)=0,这就意味着解释变量与残差项线性无关。
3.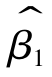 和
和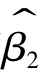 分别与残差平方和Qe相互独立;
分别与残差平方和Qe相互独立;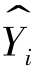 与 ei线性无关,即
与 ei线性无关,即![]()
分别求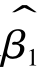 和
和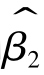 与任一残差项ei的协方差可得
与任一残差项ei的协方差可得
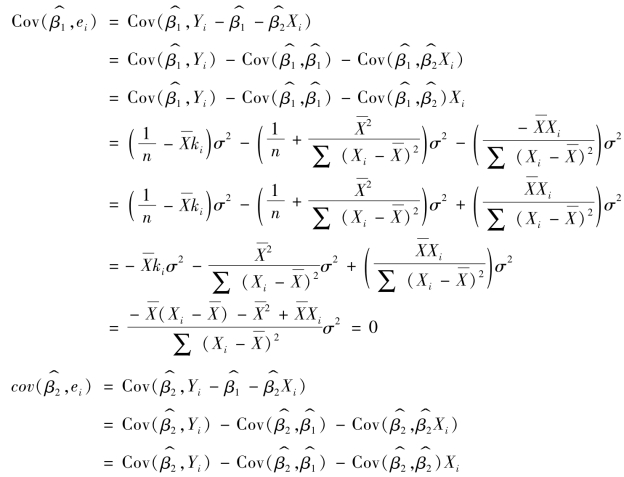
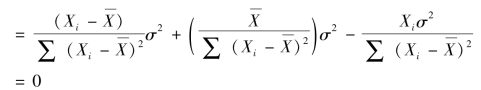
由此可见,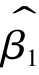 和
和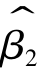 分别与任一残差项之间都是线性不相关的。
分别与任一残差项之间都是线性不相关的。![]() ,由于
,由于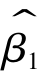 和
和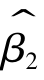 是随机扰动项的线性函数,因此,ei也是随机扰动项ui(i=1,…,n)的线性函数,估计量ei也服从正态分布,由
是随机扰动项的线性函数,因此,ei也是随机扰动项ui(i=1,…,n)的线性函数,估计量ei也服从正态分布,由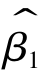 和
和 分别与任一ei线性不相关,可知
分别与任一ei线性不相关,可知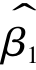 和
和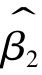 分别与任一ei相互独立,因此,
分别与任一ei相互独立,因此,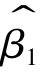 和
和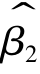 分别与残差平方和Qe相互独立。
分别与残差平方和Qe相互独立。
同时可知:
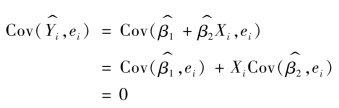
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




