总体相关系数的估计：样本线性相关系数的定义与应用

1.散布图分析

变量间的相关关系可以通过散布图进行直观分析，散布图将数据以点的形式展示在直角坐标系中，每一组观测值（Xi，Yi）对应一个点，通过散布图中点的整体变化趋势可以判断变量间相关的方向、形式，同时在可以大致判断上可以判断变量间相关的程度。

例2-1 2015年中国31个省市自治区居民人均可支配收入（X）与人均消费支出（Y）之间的散点图（如图2-1所示）。

表2-1　2015年中国31个省市自治区居民人均可支配收入（X）与人均消费支出（Y）单位：元

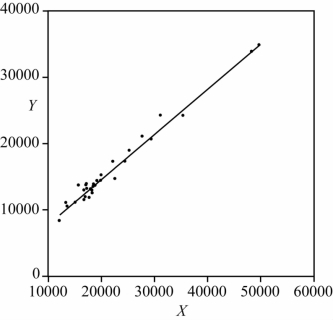
图2-1　2015年中国31个省市自治区居民人均可支配收入（X）与人均消费支出（Y）

由图2-1可见，2015年中国31个省市自治区人均消费支出随着人均可支配收入增加而增加，且整体呈现出线性趋势。常见的散布图如图2-2所示。

图2-2　散布图示意图

另外，从散布图也可以粗略判断变量间的相关程度，图2-3模拟了两个变量X与Y之间的相关关系，u为白噪声，图（a）利用Y=X+u进行模拟，图（b）利用Y=X+2u进行模拟，从模拟用的模型来看，相较于Y=X+2u，Y=X+u模型中变量Y的变异信息被X解释的程度高于Y=X+2u，因此，Y=X+u模型中X与Y之间的相关程度更高，从图2-3中可以直观的看到，图（a）中散布图绕线性函数Y=X波动的程度较低；因此，可以通过散布图中点围绕整体趋势波动的幅度粗略判断变量间相关的程度。

图2-3　两个模拟的散布图

2.相关关系的分类

（1）从相关关系涉及的变量个数来看，相关关系包括简单相关关系、复相关关系、偏相关关系和典型相关关系。简单相关关系是两个变量之间的相关关系，如身高与体重之间的相关关系；复相关关系是一个变量与多个变量之间的相关关系，如居民消费支出与可支配收入和财富拥有量之间的相关关系；偏相关关系虽然也表现为两个变量之间的相关关系，但其中一个变量与多个变量之间存在统计依存关系，如居民消费支出受可支配收入和额财富用量的影响，在此种情况下，测度居民消费支出与可支配收入的关系就需要排除财富拥有量对居民消费支出的影响，此时居民消费支出与可支配收入之间的关系称为偏相关关系；典型相关关系是两组变量之间的相关关系，如为了研究扩张性财政政策实施以后对宏观经济发展的影响，就需要考察有关财政政策的一系列指标如财政支出总额的增长率、财政赤字增长率、国债发行额的增长率、税率降低率等与经济发展的一系列指标如国内生产总值增长率、就业增长率、物价上涨率等两组变量之间的相关程度。

（2）从变量间相关关系的表现形式来看，包括线性相关和非线性相关两种情况。当变量间整体变化趋势呈现线性趋势时，变量间为线性相关（如图2-2中的（3）和（4））；当变量间整体变化趋势呈现曲线趋势时，称变量间存在非线性相关（如图2-2中的（5）和（6））。(www.xing528.com)

（3）从相关关系变化的方向看，包括正相关和负相关。当变量间整体变化趋势相同时，称变量间存在正相关（如图2-2中的（3）和（5））；当变量间整体变化趋势相反时，称变量间存在负相关（如图2-2中的（4）和（6））。

（4）从变量间相关程度来看，包括完全相关、不完全相关和不相关。完全相关时一个变量的变化完全由另一个变量决定，变量间为函数关系（如图2-2中的（1）和（2））；不相关是指变量间相互完全没有关系，彼此间互不影响（如图2-2中的（7），在此图中纵轴变量为白噪声10次观测的结果）；当变量间的相关程度介于完全相关和不相关之间时，称变量间存在不完全相关关系。

3.简单线性相关关系的度量

虽然散布图可以表征变量间相关的方向、形式，并在一定程度上表征变量间的相关程度，但由散布图得出的结论都是定性的判断，相关分析一般采用相关系数测度变量间相关的方向和程度，此处以简单线性相关系数为例，分析相关系数的性质。

对于研究的总体而言，两个相互联系的变量间的相关系数称为总体相关系数，两变量间的简单线性相关系数定义为

其中，Cov（X，Y）是变量X和Y的协方差，Var（X）、Var（Y）分别是X和Y的方差。

依据许瓦尔兹不等式易知：[Cov（X，Y）]2≤Var（X）Var（Y），因此，｜ρXY｜≤1，当变量间存在线性函数关系时，如Y=β0+β1 X，易知Cov（X，Y）=β1 Var（X），Var（Y）=β21 Var（X），那么，此时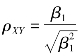，当β1＞0时，亦即X和Y之间完全线性正相关时，ρXY=1；当β1＜0时，亦即X和Y之间完全线性负相关时，ρXY=-1，当Cov（X，Y）=0时，ρXY=0变量之间线性不相关。需要说明的是，ρXY=0时，仅说明变量X和Y之间不存在线性相关关系，不代表不存在非线性关系，例如当随机变量X和Y之间满足X2+Y2=1时，易证明Cov（X，Y）=0，进而ρXY=0。

当0＜ρXY＜1时，变量X和Y间存在不完全线性正相关关系，当-1＜ρXY＜0，变量X和Y间存在不完全线性负相关关系。

由简单线性相关系数的定义（2-1）可知，ρXY=ρYX，因此在相关分析中变量间关系是对称的，这同时也说明相关分析仅探索变量间统计依存关系的方向、形式和程度，并不研究变量间的因果关系。

总体线性相关系数ρXY反映了总体两个变量X和Y的线性相关程度和方向，对于特定总体而言，ρXY是客观唯一存在的，因此，ρXY是总体参数。除非对总体进行全面调查，一般无法直接计算ρXY，通常通过给定的样本点（Xi，Yi），i=1…n，对总体相关系数进行估计，总体线性相关系数的估计量称为样本线性相关系数，其定义为

其中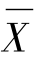，和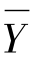分别是变量X和Y的样本均值。

利用柯西不等式容易证明。在利用给定的样本点计算出γXY后，并不能直接用其判断X和Y之间的相关性质，而需要首先检验ρXY是否显著不为0，可证明当ρXY=0时，

在给定的显著性水平下，如果已证明ρXY显著不为零，方可以通过γXY取值判定X和Y线性相关的方向和程度。γXY＞0，表示X和Y为正相关；γXY＜0，表示X和Y为负相关。γXY的绝对值越接近于1，说明两变量X和Y的线性相关程度越密切；越接近于0，说明两变量X和Y的线性相关程度越弱。一般的，当γXY＞0.8，认为X和Y之间高度相关；当0.5＜γXY＜0.8，认为X和Y之间中度相关；当0.3＜γXY＜0.5，认为X和Y之间低度相关；当γXY＜0.3，认为X和Y之间微弱相关。