概率分析在项目经济中的应用方法

概率分析的方法有很多，这些方法大多是以项目经济评价指标（主要是NPV 的期望值的计算过程和计算结果）为基础的。这里仅介绍项目净现值的期望值和决策树法，计算项目净现值的期望值及净现值大于或等于零时的累计概率，以判断项目承担风险的能力，最后简单介绍蒙特卡洛法。

1.期望值法

期望值是用来描述随机变量的一个主要参数。所谓随机变量就是这样一类变量：通常能够知道其所有可能的取值范围，也知道其取各种值的可能性，但却不能肯定其最后确切的取值。例如，有一个变量X，我们知道它的取值范围是0、1、2，也知道X 取值，0、1、2的可能性分别是0.3、0.5和0.2，但是究竟X 取什么值却不知道，那么X 就称为随机变量。从随机变量的概念上来理解，可以说在投资项目经济评价中所遇到的大多数变量因素，如投资额、成本、销售量、产品价格、项目寿命期等，都是随机变量。通常可以预测其未来可能的取值范围，估计各种取值或值域发生的概率，但不可能肯定地预知它们取什么值。由于投资方案的现金流量序列是由这些因素的取值所决定的，所以，方案的现金流量序列实际上也是随机变量。以此计算出来的经济评价指标也是随机变量，由此可见项目净现值也是一个随机变量。

从理论上讲，要完整地描述一个随机变量，需要知道它的概率分布的类型和主要参数，但在实际应用中，这样做不仅非常困难，而且也没有太大的必要。因为在许多情况下，我们只需要知道随机变量的某些主要特征就可以了，在这些随机变量的主要特征中，最重要也是最常用的就是期望值。期望值是在大量重复事件中随机变量取值的平均值，换而言之，是随机变量所有可能取值的加权平均值，权重为各种可能取值出现的概率。

一般来讲，期望值的计算公式可表达为

式中 E（X）——随机变量X 的期望值；

Xi——随机变量王的各种取值；

Pi——X 取值Xi 时所对应的概率值。

净现值的期望值在概率分析中是一个非常重要的指标。在对项目进行概率分析时，一般都要计算项目净现值的期望值及净现值大于或等于零时的累计概率。累计概率越大，表明项目承担的风险越小。

【例5-7】 某投资方案的寿命期为10年，基准折现率为10%，方案的初始投资额和每年年末净收益的可能情况及其概率见表5-7。试求该方案净现值的期望值。

表5-7　方案的不确定性因素值及其概率

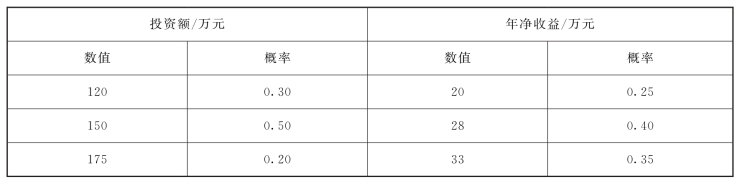
【解】 组合投资额和年净收益两个不确定性因素的可能情况，该方案共有9种不同的组合状态。例如，初始投资额为120万元、年净收益为20万元的概率是0.30×0.25＝0 075，此时方案的净现值为

NPV＝－120＋20×（P/A，10%，10）＝2.89（万元）

同理计算各种状态的净现值及其对应的概率，详见表5-8。

表5-8　方案所有组合状态的概率及净现值

于是，可求出净现值的期望值：

E（NPV）＝2.89万元×0.075＋52.05万元×0.12＋82.77万元×0.105＋（－27.11）万元×0.125＋22.05万元×0.2＋52.77万元×0.175＋（－52.11）万元×0.05＋（－2.95）万元×0.08＋27.77万元×0.07＝24.51万元

净现值的期望值在概率分析中是一个非常重要的指标，在对项目进行概率分析时，一般除了计算项目净现值的期望值之外，还可以计算净现值大于等于零时的累计概率，累计概率越大，表明项目的风险越小。对此例，按净现值从小到大排序，同时计算累计概率，见表5-9。

表5-9　方案现值的排序及累计概率

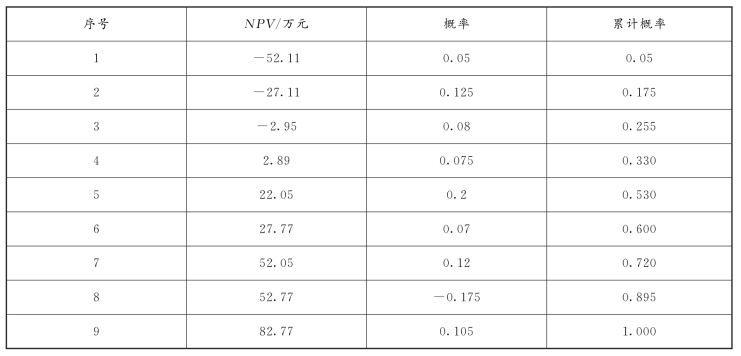
再依据线性内插的思路，计算NPV≥0的累计概率：

NPV≥0的累计概率越大，表明项目的风险越小。

当然，方案决策时应根据具体情况的灵活选择指标并对之应用期望值法。

2.决策树法

决策树是直观运用概率分析的一种图解方法，因其运用树状图形来做多方案的分析和择优而得名。决策树是将各种可供选择的方案以及影响各备选方案的有关因素（如自然状态、概率、损益值等）绘成一个树状图（图5-7），这个树状网络图从左向右展开，一般根据期望值法计算每一个方案的期望损益值进行决策。决策树法特别适用于多阶段分析。

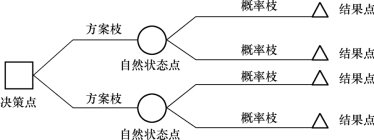
图5-7　决策树结构图

决策树一般由三种点、两类枝组成，三种点即决策点、自然状态点、结果点；两类枝即方案枝和概率枝。决策点用“□”表示，是对多种可能方案择优的结果；从决策点引出若干条分枝，每条分枝代表一个备选方案，此即方案枝；在方案枝末端连接自然状态点，以“○”表示，代表备选方案的期望损益值；从自然状态点引出的各条分枝即为概率枝，每一分枝代表一种自然状态可能出现的概率；在每条概率枝的末端以结果点“Δ”结束，并标注各方案在相应自然状态下的损益值。

应用决策树进行决策一般步骤如下：(www.xing528.com)

（1）绘制决策树。根据决策问题的具体条件，由左到右逐步展开绘制决策树，为便于随后的分析、择优，对“□”（决策点）和“○”（自然状态点）混在一起进行编号，编号的顺序是从左到右、从上到下。

（2）运用期望值法进行决策。逆着编号逐步计算各“○”（自然状态点）的损益期望值，遇到“□”（决策点），则比较损益期望值的大小，“剪枝”删去被淘汰的方案。

（3）“□”（决策点）上只留有被选中的最佳方案一枝。

决策树法可分为单级决策和多级决策两种。把在整个决策期中只需要进行一次决策，就可以选出最佳方案的决策称为单级决策；当决策问题比较复杂时，就需要进行一系列的决策过程才能选出最佳方案，以达到决策目标，这种决策称为多级决策。多级决策是由若干个单级决策构成的，因而其与单级决策所不同的是多几个决策点，分为几段，每一段都是一个单级决策。

决策树能使决策问题形象直观，思路清晰，特别是在多级决策活动中，能起到层次分明、一目了然的作用，其对于集体思考与讨论以及计算有很大帮助。决策树应用较广泛，也是十分有效的辅助决策的工具。

【例5-8】 现有两个建厂方案：建大厂、建小厂。建大厂需投资300万元，建小厂需投资160万元，大厂或小厂的经营期均为10年。经市场调查，可能的自然状态和年收益见表5-10。决策建厂方案。

表5-10　可能自然状态和年收益

【解】 绘制的决策树如图5-8所示。

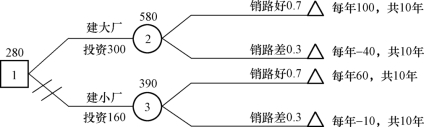
图5-8　决策树（单位：万元）

用期望值准则决策：

E1＝[60×0.7＋（－10）×0.3]×10＝390（万元）

E2＝[100×0.7＋（－40）×0.3]×10＝580（万元）

E3＝max{390－160，580－300}＝max{230，280}＝280（万元）

所以，建大厂10年利润期望值为280万元。

3.蒙特卡洛法

蒙特卡洛法是一种用随机模拟（仿真试验）不确定性问题的方法。用蒙特卡洛法进行风险分析，计算工作量很大，因为要获得一个随机因素（不确定因素）的概率分布就要进行上百次甚至更多的反复模拟试验。试验次数越多，形成的概率分布就越接近于真实情况。实际工作中可以借助计算机进行模拟计算。

蒙特卡洛法实施的一般步骤如下：

（1）确定风险随机变量。通常运用敏感性分析确定风险随机变量。

（2）确定风险随机变量的概率分布。

（3）通过随机数表或计算机为各随机变量抽取随机数。

（4）根据风险随机变量的概率分布将抽得的随机数转化为各输入变量的抽样值。

1）如果是离散型随机变量的模拟，则用随机数作为随机变量累计概率的随机值，结合累计概率图，画一条水平线与累计概率折线相交的交点对应的横坐标值即为输入变量的抽样值。

2）如果是正态分布随机变量的模拟，则随机数（RN）作为随机变量累计概率的随机值，这样，每个随机数都可找到对应的一个随机正态偏差（RND），对应的随机变量的抽样结果可通过下式求得：

3）如果是具有最小值a和最大值b 的连续均匀分布随机变量的模拟，随机数（RN）作为随机变量累计概率的随机值，其中，设RNM 表示最大随机数，对应的随机变量的抽样结果可通过下式求得：

（5）将抽样值组成一组项目评价基础数据。

（6）选取经济评价指标，如内部收益率、财务净现值等，根据得到的基础数据计算出一组随机状况下的评价指标值。

（7）重复上述过程，进行多次反复模拟，得出多组评价指标值。

（8）整理模拟结果所得评价指标的期望值、方差、标准差和它的概率分布及累计概率，绘制累计概率图，同时检验模拟次数是否满足预定的精度要求。根据上述结果，分析计算项目可行或不可行的概率。