资金有限的独立方案的比较选择

一般情况下，由于项目的经济条件有限，能够采用的方案数目多少会受到项目财力、物力和人力的限制，这样就使独立方案的比选成为有约束条件的选择。在资金总额约束的条件下，项目方案比选的实质是排列各方案的优先次序，使净收益大的方案优先采纳，在不超过有限资金总额的条件下，选取能够带来总收益最多的一组方案。常用的资金有限独立方案的比选有两种方法，即独立方案互斥化法和效率指标排序法。

1.独立方案互斥化法

独立方案互斥化的原理是将独立方案的所有组合列出来，使每个组合形成一个组合方案（其现金流量为被组合方案现金流量的叠加），因这些组合方案之间是互斥关系，故被称为组合互斥方案。由于是所有可能的组合，则最终的选择只可能是其中一种方案组合，因此，所有可能的组合方案形成了互斥关系，可按互斥方案的比选方法确定最优的方案组合。最优的方案组合即是独立方案的最佳方案选择。

用净现值指标评价的基本步骤如下：

（1）分别对各独立方案进行绝对效果检验，即剔除NPV＜0，或IRR＜ic 的方案。

（2）对通过绝对效果检验的独立方案，列出所有可能的方案组合，将所有的组合按初始投资额从小到大的顺序排列。

（3）排除初始投资额超过投资资金限制的方案组合。

（4）对所剩的方案组合按互斥方案的比选方法确定最优的方案组合，可用净现值法判定，即分别计算各方案组合的净现值，以净现值最大者为最佳组合，也可用增量内部收益率法选择最佳方案组合，不过其结论和净现值法是一致的。

【例3-14】 有三个独立方案A、B和C，寿命皆为10年，现金流量见表3-12。基准收益率ic＝10%，投资资金限制为7 000万元。要求选择最佳方案组合。

表3-12　独立方案现金流量 万元

【解】 首先分别计算各独立方案的净现值，剔除单一方案不可行者。按照所有可能方案的投资额的大小排序（包括0方案），见表3-13。

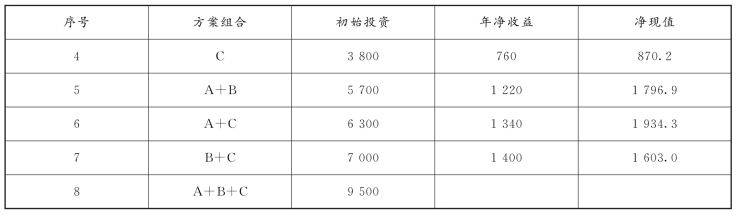
表3-13　组合互斥方案现金流量计算 万元

续表

(www.xing528.com)

由于方案组合A＋B＋C的投资额为9 500万元＞7 000万元，故可不计算此组合。观察对比表3-13中各组合的净现值，A＋C的净现值最大且大于0，所以，A＋C为最优方案组合，A 方案和C方案是最优的选择。

2.效率指标排序法

效率指标排序法包括内部收益率排序法和净现值率排序法。内部收益率排序法是根据资源效率指标的大小确定独立项目的优先顺序，然后根据资源约束条件确定最优项目组合。

【例3-15】 有6个独立方案的现金流量见表3-14，寿命期均为6年，基准收益率ic＝10%。①若资金限制为520万元，选择哪些项目最有利？②若资金限制为500万元，选择哪些项目更有利？

表3-14　独立方案现金流 万元

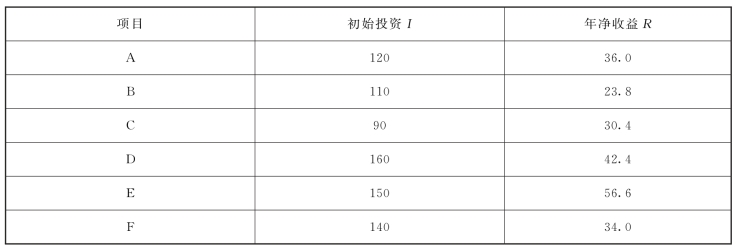
【解】 首先求出各个项目的内部收益率，内部收益率可按照下式计算：

－I＋R(P/A,IRR,6)＝0

IRRA＝20%,IRRB＝8%,IRRC＝25%,IRRD＝16% ,IRRE＝30%,IRRF＝12%。

图3-9表示各个项目按照内部收益率高低的排序，纵坐标表示内部收益率，横坐标表示投资额I的累计值，虚线表示基准收益率水平ic。

（1）若资金限制为520万元，由图3-9可知，按照内部收益率的高低优先选择（E、C、A、D），且（E、C、A、D）4个项目的投资额刚好等于520万元。B 项目IRRB＝8%＜ic，故无论有没有剩余资金都应该被淘汰，F 项目虽然IRRF＝12%＞ic，但是由于资金有限，不得不放弃。故最终的选择为（A、C、D、E）4个项目。

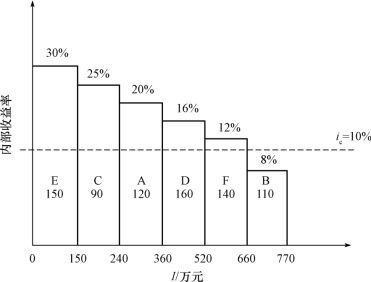
图3-9　项目优劣顺序图

（2）若资金限制为500万元，则（E、C、A）项目可以首先选择，投资为360万元，剩余140万元资金，由于项目的不可分割性，D项目不能被选中，但是下一个项目F的内部收益率IRRF＝12%＞ic，且资金刚好为140万元，故最优的项目组合为（A、C、E、F）4个项目。

净现值率排序法和内部收益率排序法具有相同的原理：计算各方案的净现值，排除净现值小于零的方案，然后计算各个方案的净现值率（净现值率＝净现值/投资额的限制），按净现值率从小到大的顺序，一次选取方案，直至所选取方案的投资额之和达到或最大限度地接近投资限制。