如何正确测量民意误差？

Naked Statistics

民调结果显示，有89%的美国人不相信政府会做正确的事，有46%的美国人认可奥巴马的工作表现。这个结果可以代表美国人的真实想法吗？

2011年下半年，《纽约时报》头版报道了“美国全国陷入了对未来的深深忧虑和怀疑中”，作者对美国人的心理进行了探究，整理了美国公众对于奥巴马政府的表现、社会财富分配等众多问题的普遍看法。下面，我们就来了解一下2011年秋天美国人想要表达的想法：

● 有高达89%的美国人不相信政府会做正确的事—美国政府遭遇了有记录以来最严峻的一次信任危机。

● 有2/3的美国公众认为，财富应该在美国得到更加公平的分配。

● 有43%的美国人说他们大体上认同“占领华尔街”运动所宣扬的观点（“占领华尔街”是一场发轫于纽约华尔街并迅速波及全美和其他国家的自发性抗议活动）。此外，还有更多的美国人（46%）认为“占领华尔街”运动中抗议人群的观点“基本上反映了绝大多数美国人的观点”。

● 有46%的美国人认可奥巴马作为美国总统的工作表现，同样有46%的美国人不认可奥巴马的工作表现。

● 仅有9%的美国公众认可美国国会的工作。

● 虽然距离下一次的美国总统初选只剩下不足两个月的时间，但是，还有将近80%的共和党选民觉得“现在就决定支持谁为时尚早”。

在美国总统选举年即将到来之际，这些引人入胜的数据可以为人们提供一些有意义的参考，让读者窥见美国人作为一个整体的所思所想。但是，总会有人忍不住要问：我们是如何知道这些情况的？美国的人口数以亿计，为什么我们就能对他们的想法做出如此精确的判断？我们怎么知道这些言之凿凿的判断是否正确？

答案当然是4个字：民意测验。上述例子的民意测验是由《纽约时报》和哥伦比亚广播公司（CBS）共同主导的（连两家彼此竞争的媒体都必须在某个民调项目上通力合作，可见要主导一个方法论上可行和完善的全美国性民调有多么“浪费资金”）。对于民意测验的结论，我想大家肯定不陌生；如果告诉大家民意测验的方法论其实是统计推断的另一种形式，大家会不会有一种恍然大悟的感觉？民意测验（或民调）就是基于从某个人口群体中所抽取的人口样本的观点所做出的推断。

民意测验的力量与前几章有关的样本案例如出一辙：中心极限定理。假如从美国选民（或其他任意的一个群体）中选取一个大型的代表性样本，那么我们完全可以合理地认为这个样本与其所在的群体具有相似性。假如正好有1/2的美国人不赞同同性婚姻，那么在一个数量为1 000人的样本中，会有多少人不赞同同性婚姻呢？最佳猜测当然是500人。

一个更加符合民意测验的想法是将上面的例子反过来思考。如果我们有一个数量为1 000人的样本，其中有46%的人不认可美国总统奥巴马的工作表现，那么我们就能从中推理出全体美国人对这个问题的态度。事实上，我们还可以计算出样本结果大面积偏离整体的概率。如果你在一个民调结果里看到“误差幅度为±3%”的字眼，其实就跟我们在上一章所讲的“置信区间为95%”是一个道理。95%的置信区间意味着假如从同一个群体中重复进行100次不同的抽样，我们可以预测其中有95次测验结果会位于该群体真实感受±3%的范围。在《纽约时报》和CBS的民意测验中，有关工作表现的问题，我们有95%的把握认为所有美国人中不赞同美国总统奥巴马工作表现的比例会在46%±3%的范围内，即介于43% ～ 49%。如果你在读报时看得仔细，会发现这篇报道的下方有一行小字（我强烈建议大家去读一读）是这样写的：“理论上说，民意测验结果有95%的概率在实际情况（即采访所有美国成年人所得出的结论）±3%的范围内浮动。”

民意调查和其他形式的抽样之间最根本的区别就在于，我们所关心的前者的样本数据不是平均数（如187磅），而是一个百分比（如47%的选民、0.47等）。除此以外在其他方面，两者的流程是类似的。当我们掌握了一个数量巨大、具有代表性的样本（民意样本）之后，我们便可以预测样本里持某种观点的人数比例（如9%的人认为美国国会在管理国家事务中发挥了良好的作用），约等于所有持该观点的美国人占美国总人口的比例。这与认为一个包含1 000名美国男性样本的平均体重约等于所有美国男性的平均体重并无二异。但是，不同的样本对于美国国会工作的认可程度表现在百分比方面还是会有所不同，这和不同的随机样本中1 000个男性的平均体重也会稍许差别是一样的。如果《纽约时报》和CBS进行第二次民意测验，也就是对另外1 000名美国成年人提出同样的问题，那么第二次的民调结果与第一次的结果完全相同的概率非常低。但与此同时，我们也不应该指望第二次民调结果与第一次的结果大相径庭。用一个比喻形容，就是你舀了一勺汤尝了尝，然后用汤勺搅动了一下汤锅，之后再舀一勺汤，这两勺汤的味道应该是差不多的。标准误差所要传达的就是不同样本平均值和不同民调结果的离散程度。

百分比的标准误差计算公式与之前介绍的有细微差别，但其中的原理是一样的。对于任意一个随机抽取的样本而言，标准误差等于 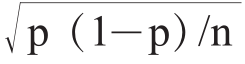，其中p代表某个特定观点的回应者比例，（1–p）代表不同观点的回应者比例，n为样本中所 有回应者的数量。而且由于n处于分母的位置，因此样本量越大，标准误差越小。而且当p与（1–p）的差距越来越大时，标准误差也会变得越来越小。举例来说，当有95%的回应者表达相同的观点时，其样本的标准误差就会小于回应者观点只有50%的相同率的样本的标准误差。这就是纯数学，0.05×0.95 = 0.047，0.5×0.5 = 0.25，分子的数字越小，计算得到的标准误差也越小。

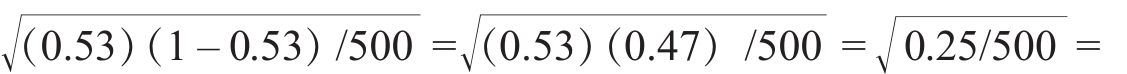
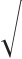
举个简单的例子，假设在一次“选举后测验”中，在选举当天投出选票的500位选民里有53%投给了美国共和党候选人，45%投给了美国民主党，还有2%投给了第三方的候选人。如果以美国共和党的支持率作为参照，那么这次“选举后测试”的标准误差就是 0.022 36。

为了方便起见，我们将这次的“选举后测试”的标准误差约等于0.02。到现在为止，这只是一个数字，要怎样才能赋予0.02这个数字更多的意义呢？假如这次民意测验刚刚结束，在一家电视台工作的你就急于在最终结果出来之前向全美国观众率先宣布这场比赛的赢家是谁。你现在已经算得上是一名“半专业”的数据分析师了（因为你已经读完了本书2/3的内容），节目制片人向你咨询：我们能否以这次“选举后测试”的结果作为宣布共和党获胜的依据？

你解释说，这要看你在这条选情预测新闻里的“置信区间”有多少了。更具体地说，你愿意为播出内容的错误承担多大的风险？需要记住，标准误差为样本比例（“选举后测试”）是否接近于现实中的人口比例（选举结果）提供了理性的概率参考。我们已知的是，样本比例约有68%的概率落在最终结果一个标准误差的范围内（在这个例子中指的是共和党53%的选民支持率），因此，你可以告诉你的制片人，你有68%的把握认为共和党会获得53%±2%的支持率，也就是51%～55%。与此同时，“选举后测试”显示民主党候选人获得了45%的选票，假设民主党的支持率有相同的标准误差（至于为什么可以这样简化，我等一下会向大家解释），那么我们也可以有68%的把握声称，民主党会获得45%±2%（43%～47%）的支持率。根据这一计算，我们的结论是共和党会在选举中获胜。

图文组的同事会在第一时间制作出一张适合于电视播放的立体统计图，这样你就可以显示在荧屏上给观众演示了。这张统计图里肯定会包含以下信息：

共和党 53%

民主党 45%

独立党派 2%

（误差幅度±2%）

首先，你的制片人面对这样的一个结果肯定会印象深刻并且兴奋不已，很大程度上是因为上面的这张统计图竟然是彩色3D版的，而且还能在屏幕上进行360°旋转。但是，当你向她解释道，“选举后测试”的结果约有68%的概率落在真实情况一个标准误差的范围内时，这位两次被法庭强制要求参加愤怒管理课程的制片人在脑子里迅速作了一个减法：那剩下的32%是什么情况？

接下来，你解释说会有两种可能：（1）共和党的支持率比民调结果更高，在这种情况下我们的预测依旧是正确的；（2）也有一定的可能性是民主党获得了比民调高得多的支持率，如果是这种情况，就意味着之前彩色的、可以旋转的3D图错误地预测了选举的获胜方。

制片人听完后一言不发，随手将桌上的一个咖啡杯扔了出去，杯子在空中划出了一条完美的弧线，并最终落在了房间的另一端，摔得粉碎。接着，她大声呵斥道：“我们怎么才能保证播出的是一个正确的结果？”

作为统计学专家，你指出，除非将所有选票都清点出来，否则没有人能够准确无误地预测选举结果。但你还是将置信区间扩大到了95%，在这种情况下，那张3D统计图出错的概率就降到了5%。

制片人点上了一支烟，看上去比刚才放松了一些。你决定还是不提醒她办公场所禁止抽烟的规定，因为上一次就是因为这句善意的提醒而引发了一场灾难。但是，有一些坏消息是不得不说的。电视台在播出新闻时如果要让自己的可信度提升，就必须扩大“误差幅度”，一旦这样做了，就意味着选举结果中不再有一个清晰的赢家了。你将新制作好的统计图拿给你的制片人看：

共和党 53%

民主党 45%

独立党派 2%

（误差幅度±4%）

由中心极限定理我们得知，样本比例约有95%的概率会落在真实群体比例的两个标准误差（这个例子中这一比例为4%）的范围内。因此，假如我们想要增加“选举后测试”的可信度，就必须减少我们对结果准确度的野心。如上述所示（请原谅我没有为大家展示炫目的彩色3D和旋转效果），电视台可以有95%的把握向观众播报，美国共和党候选人的得票率为53%±4%，即在49%～57%的区间范围内；与此同时，美国民主党候选人的得票率为45%±4%，占全体选票的41%～49%。

是的，我们现在又有了一个新问题。如果置信区间扩大到了95%，我们就无法推翻两党候选人打成平手（各获得49%选票）的可能性。这是一个无法避免的妥协，在没有新数据补充的情况下，如果想要提高民调结果的正确率，就只能降低预测的精度。举一个与统计学无关的例子，假如你告诉你的朋友，你“确定”托马斯·杰斐逊是美国的第三或第四任总统，你如何让自己的历史知识可信度更高？扩大范围吧！你可以“绝对肯定”地说托马斯·杰斐逊是美国前5位总统中的一位。

制片人让你打电话订一个比萨，作好通宵加班的准备吧。就在这个时候，统计学的“万丈光芒”又照在了你的身上。第二次“选举后测试”的结果出现在你的办公桌上，这一次的样本数量为2 000人，占比结果是：共和党（52%）、民主党（45%）、独立党派（3%）。你的制片人已经彻底发疯了，因为这一次的民意测验显示两个主要党派之间的差距进一步缩小了，也就是说，在官方结果出来之前对选举进行预测变得难上加难。但此时你（英勇地）指出，这次的样本数量是上一次的4倍，因此标准误差会大大缩小，共和党候选人的新标准误差为 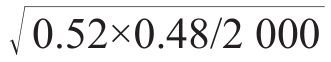= 0.1。(www.xing528.com)

假如制片人此时还愿意接受95%的正确率，那么你便可以大声地宣布共和党将会赢得选举。在新的0.1的标准误差的前提下，95%的置信区间意味着共和党候选人获得了52%±2%，即50%～54%的选票，民主党获得了45%±2%，即43%～47%的选票。两个置信区间之间不再有重叠，你可以在电视上恭喜美国共和党候选人了，而且这次预测正确的概率超过95%。

但在这个例子中，你还可以做得更加完美。中心极限定理告诉我们，样本结果位于真实情况3个标准误差范围以内的概率为99.7%。如果将置信区间扩大到99.7%，那么两党的投票情况是：共和党获得的选票为52%±3%，即49%～55%；民主党获得的选票为45%±3%，即42%～48%。介于两党的结果依然没有重叠，你便放心地在电视上预测共和党的胜利，你和制片人基本上不可能因为误播而被辞退，所以记得一定要请组织那次2 000人民意测验的同事吃饭。

你可以看到，样本数量越大，标准误差就越小，这也是为什么大型的全美民意测验的结果往往准得惊人。同理，一个小容量的样本会使得标准误差变大，从而导致一个更大的置信区间（用民意测验的专业术语来说，就是“抽样误差范围”）。《纽约时报》和CBS联合民意测验报告的小字部分内容指出，有关美国共和党初选问题的抽样误差为5%，而其他问题的抽样误差只有3%。由于报名参加共和党初选的选民数量有限，因此该问题组的抽样人数只有455人（而其他问题组的抽样人数都达到了1 650人）。经意识到了，在上述的选举例子中，共和党和民主党按理来说应该有着各自不同的标准误差。再来看一下这个公式：SE 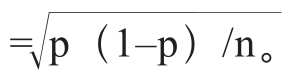两党候选人的样本数量n是一样的，但p与（1–p）会有所差别。在第二次选举后测试（有2 000名参与者）中，共和党的标准误差为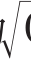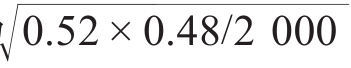= 0.011 17，民主党的标准误差应该是 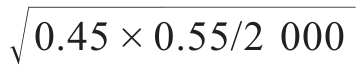= 0.111 2。当然，无论是用作什么，这两个数字都不会对结果产生不同的影响。因此，我采取了一个比较常用的做法，就是取两者中略大的那个标与前几章的内容一样，我在本章中对很多内容进行了简化处理。可能大家已准误差作为所有候选人的共同标准误差，假如真有什么不妥之处，那也只会让我们的置信区间更加严格。

许多涉及多个问题的全美国性民意测验还会更进一步。以《纽约时报》和CBS联合民调为例，严格来说，根据受访者的答案，每一个问题的标准误差都应该是不同的。例如，在9%的公众认可美国国会处理国家事务的能力和46%的公众认可美国总统奥巴马的工作表现这两个结论中，前者的标准误差应该低于后者，因为0.09×0.91的结果要小于0.46×0.54—0.081 9＜0.248 4。

如果每一个问题都搭配一个不同的标准误差，那么整个报告就会变得混乱不堪，不利于结论的提取，因此像这类民意测验，通常都会假设所有问题的样本比例为0.5（50%）—让标准误差达到一个最大值，然后再用这个标准误差计算出整个民意测验的样本误差范围。

如果处理得当，民意测验会是一个不可思议的统计工具。盖洛普民意测验机构的主编弗兰克·纽波特说，一个针对1 000人的民意测验能够为我们提供有关整个国家的有意义的和准确的信息。从统计学的角度，他的说法是正确的。但是，为了能够获得那些有意义的和准确的结果，我们必须合理设计民调流程，正确分析数据并得出结论，这两件事都是说起来容易做起来难。一个错得离谱儿的民调结果通常并不是因为数学不好而导致标准误差计算错误，而是因为一个有偏见的样本或不合理的问题设计，或者二者均有。当进行一项民意测验或采用别人的民调成果时，我们应该问问自己如下这几个涉及方法论的关键性问题。

这个样本能正确地反映目标群体的真实观点吗？许多与数据有关的常见挑战都已经在前文中介绍过了。然而，我还是孜孜不倦地指出选择性偏见的危害，尤其是自我选择。有一些民意测验依赖的是那些选择进入样本的个人，如听众来电类广播节目或自愿填写的网上调查问卷，这些民意测验只能获取那些愿意花时间和精力来表达观点的人的信息。他们有可能是对某个问题有着强烈看法的人，或者是正好拥有大量空闲时间的人。无论是哪一种人，都不太可能代表广大公众的观点。我有一次被邀请作为嘉宾参加某听众来电节目，有一位打进电话的听众大声地批评我的观点是“多么不正确”，为了表达他的异议，他是特地将车驶离高速公路后将车停在路边，在一个电话亭拨打的电话。我更愿意假设的是，其他那些选择继续开车的听众之所以没有驶离高速公路并打进电话，是因为他们的看法与之前的那位听众不一样。

任何一种将群体中的某类人排除在外的观点收集方法，都有可能造成偏见。举例来说，手机的出现给取样方法论增添了新的内容，但同时也让这个过程变得更加复杂。专业的民意测验机构在目标人群的代表性样本的抽样方面，可以说是不遗余力。《纽约时报》和CBS的联合民调就是基于电话访问，在6天的时间里，他们通过电话调查了1 650名美国成年人，其中有1 475名美国成年人声称自己是登记选民。

至于具体是如何抽样的，我只能进行一个大概的猜测，绝大多数的民意测验采用的都是如下的技术。为了保证接电话的人能够代表美国人口，抽样过程是从概率开始的—相当于从口袋中摸彩球。电脑会随机抽取一个座机电话交换机组（电话交换机是汇集电话线路并完成用户之间通话的设备，在美国，一个电话交换机包含一个区号以及电话号码的前3位），通过在美国约6.9万个家庭交换机组里随机选取与电话人口比例一致的用户样本，就能大体上形成一个具有人口地域代表性的样本分布。请看说明：“电话交换机的选择考虑了每个地区的电话用户占美国电话用户数量的比例。”每组被抽中的交换机由电脑随机加上4位数字，以形成一个完整的电话号码，最后出现在被呼叫家庭的名单里。同时，该调查还包括了“手机号码的随机拨打”。

每一个拨出去的号码都应该有一位对应的成年人接听，但如何选取也应该有一个“随机的程序”，如要求让当前家中年纪最小的成年人来回答问题。这一个程序经过优化，能够让接听人的年龄、性别比例更加接近真实的成年人口。最重要的是，调查人员会尝试在一天的不同时刻拨打电话，以确保被挑中的电话号码能够打通。这些不断重复的操作—包括重拨某个电话多达10多遍—都是获得一个平衡样本不可缺少的重要组成部分。如果只是在工作时间随机拨打电话，能打通最好，打不通就更换其他号码，直到凑齐所需的样本数量，这样做当然在操作上更加容易实现，也更省钱，但这样的一个样本很有可能会存在偏差，在家接听电话的人很有可能大多是失业者或老人等。如果你只是想证明民意测验结果是美国总统奥巴马在失业人口、老人以及热心接听陌生来电人群中的支持率为46%的话，那你这样做是可以的。

检验民意测验是否正确有效的另一个指标是：被选中的电话号码中有多少接听者最终能够完成电话调查？假如完成率很低，那么就要小心会出现样本偏见了。不接受电话调查的人越多，或者家中电话一直处于无人接听的状态，那么这些人就越有可能与那些完成调查的人存在本质区别。民调策划人可以通过分析那些无法联系上的电话用户的已知信息来决定是否存在“无应答偏见”，这些人是否都住在同一个地区？他们拒绝采访的原因是不是都是类似的？他们是不是大多来自同一个种族、民族或收入群体？通过此类分析，我们便能够知道较低的回应率是否会影响到某次民意测验的结果。

采访过程中的问题设置能得出对研究课题有用的信息吗？探析公众观点可比计算考试成绩或测量身高和体重要复杂、细致得多了。民意测验的结果对于问题的设置和提问方式极其敏感。让我们来举一个简单的例子：有多少比例的美国人支持死刑？正如本章内容所示，有很大一部分观点坚定的美国人支持死刑。根据盖洛普民调机构的调查，从2002年起，每年的民意测试都显示有超过60%的美国人支持对谋杀犯判处死刑。美国人对死刑判决的支持率一直在一个很小的范围内变动，最高时的支持率为2003年的70%，其他时候支持率也曾低至64%。但民调数据的结果是很清楚的：大多数美国人都支持死刑。

事实是这样的吗？当把无假释终身监禁作为选项放入问题中去之后，美国人对于死刑的支持率就大大下降了。2006年的盖洛普民调发现，只有47%的美国人认为对谋杀犯判处死刑是合适的，而有48%的受访者选择了终身监禁。这可并非某场晚宴上的统计学玩笑，这意味着当无假释终身监禁作为一个可靠的选择时，多数美国人将不再支持死刑。在作公众调查的过程中，问题的设置以及提问的方式都会对结果产生巨大影响。

政客们就常常利用这一点来获得对自己有利的民调结果。例如，选民们对“免税”一词的好感度就高于“减税”，其实这两个词说的是同一个含义。同样的，相比起“气候变化”，选民们更加关心“全球变暖”，虽然后者只是前者的形式之一。政客们总是通过非中性词的使用来操纵选民的反应。如果一个中立、正直的民调机构想要获得正确有效的结果，它们必须警惕那些可能会影响反馈信息准确性的用语。同样的，如果想要比较在不同时间点获得的调查结果，比如2012年和2013年消费者对经济的看法，那么这两个时段的采访问题就应该保持相同或相似。

像盖洛普这样的机构会经常组织开展“分离样本测试”，也就是将同一个问题的不同问法用在不同的样本人群里，以便判断用词上的小小变化到底会不会影响回应者的答案。对于盖洛普民调机构专家弗兰克·纽波特而言，每一个问题的答案都是有意义的数据，就连那些看上去似乎有些矛盾的答案也不例外。美国人对于死刑的态度在终身监禁的刑罚颁布之后发生了剧烈改变，这其中就透露了一些重要的信息。纽波特说，关键在于要在一个大背景下看待民意测验的结果。对于一个复杂的话题，只看一个问题或一次民调结果是不可能完全看透公众的心理的，此时更需要有大局观和联想力。

受访者说的就一定是真的吗？民意测验就像是网恋，在对方所提供的信息里总是有那么一点儿“言不由衷”的成分。我们都知道，人都有撒谎的时候，尤其是当问题比较尴尬或敏感时。受访者可能会夸大他们的收入，或在某个月的做爱次数上“修饰一番”；他们可能会不好意思地承认自己没有投票；在表达不受欢迎或社会认可度低的观点之前他们还会犹豫。正是因为这些，一个民意测验先期准备得再充分、设计得再合理，也依然需要受访者的诚实回答。

选举民调尤其关键的一步是，将那些不会在选举日当天去投票站投票的美国公民筛选出来（因为如果我们想预测某次选举的胜利者，那么那些不打算去投票的人的观点对于我们来说就是无关紧要的）。作为个人而言，他们总是会说自己会去投票，因为他们觉得这是民调公司愿意听到的答案。但是有研究表明，那些自称会去投票的人中有1/4～1/3的人最终没有投票。为了减小这类抽样偏见对民调结果的影响，一种方法是向受访者提问他们是否参加了上一次或前几次的选举投票，那些每场投票都参加的受访者最有可能在未来的选举中投票。如果担心受访者会羞于表达某个社会接受度不高的观点，例如对某个激进组织或民族群体的负面印象，民调人员会采用迂回的问法，如“你身边有认识的人”持有这种观点吗？

历史上最触人神经的一次民意测验来自芝加哥大学全美国民意研究中心（NORC）的一个研究项目，课题名称为“性的社会组织：美国人的性行为”，很快便成为人们熟知的“性调查”。这项研究的官方描述包括“构成性交易的行为结构”、“一生中的性伴侣组合过程和行为方式”等用语。用最简单的话来概括这项研究就是：谁在跟谁做爱，以及多长时间做爱一次。这项发表于1995年的研究，其目的不仅仅告诉我们身边人的性行为，同时也是为了预测美国人的性行为是否会以及如何影响到艾滋病的传播。

倘若美国人连没去投票这类事情都难以承认，那么可以想象他们在描述自己的性行为时内心的那种纠结，尤其是当这些问题涉及不正当行为、不忠以及其他隐私的内容时。他们的调查方法非常引人注目，调查样本为3 342名成年人，这些人代表了全体美国成年人群体，每一位受访者都要经过长达90分钟的采访，其中有将近80%的受访者完成了全部问题，研究人员在此基础上得出了一份有关美国人性行为的准确报告（至少在1995年的时候是这样的）。

鉴于大家已经硬着头皮读完了一整章有关民意测验方法论的内容，而且基本上“啃”完了一本有关统计学的书，到了应该“犒劳”大家的时候了，一起来看看这项“性调查”都发现了什么吧（其实都不是什么“骇人听闻”的结论）。正如一位读过这份报告的人所说：“美国人的性行为比我想象的‘逊色’太多了。”

● 人们通常与自己的“同类”做爱，有90%的夫妻都来自于相同的种族，拥有相同的宗教信仰、社会阶级和相仿的年纪。

● 大多数人的性生活频率为“一个月若干次”，至于“若干次”是几次，这个范围就大了。关于受访者从18岁开始有过的性伴侣数量，有的人没有性伴侣，有的人的性伴侣人数多达1 000个，绝大多数人的性伴侣人数在这两者之间。

● 有差不多5%的男性和4%的女性有过同性性行为。

● 80%的受访者在过去一年里，只有一个甚至没有性伴侣。

● 拥有一个性伴侣的受访者要比那些一个都没有或者同时拥有多个性伴侣的人更快乐。

● 1/4的已婚男性和10%的已婚女性承认自己曾经“出轨”。

● 绝大多数人在做爱方面还是比较传统的，男女之间最有吸引力的做爱方式依然很传统。

对于这份知名的“性调查”，有一句简单但却有力的评论：调查结论中的那句“调查的准确性保证结论能够代表全体美国成年人的性行为”是建立在两个前提之上的，受访者是从全体美国成年人中正确抽取的样本，受访者提供了诚实准确的答案。其实，我们也可以用这句话来概括整章的内容。对民意测验最为直观的感受是，人们会怀疑就凭这样一些人的回答真的能知道大部分群体中的人心里到底是怎么想的？回答这个问题其实很容易，统计学最基本的原则之一就是一个正确抽取的样本相似于其所在的群体。民意测验真正的挑战有两个：设计并选取正确的样本；用恰当的方式从该样本中获取合适的信息，以准确地反映他们的真实感受。

本章补充知识点

下面为大家解释一下，为什么当某个回答占所有受访者人数的比例接近50%时（同时意味着1– p也接近50%），标准误差会达到最大。先假设你正在美国的北达科他州进行两项民意测验。第一项民意测验的目的是弄清该州民主党和共和党的人数比例。假设这个州真实的两党人数正好各占50%，但你的民调结果却显示为60%的共和党人和40%的民主党人。因此，你的结果距离真实情况出现了10%的巨大误差。但是，你在这个统计过程中并没有犯下什么难以饶恕的数据收集错误，你只是使共和党人增多了20%，使民主党人减少了20%。这种计算错误时常会发生，有时候即使是一个方法设计良好的民意测验也无法避免。

你的第二项民意测验旨在获取生活在北达科他州的印第安人占该州总人口的比例。假设真实情况是印第安人占全州人口的10%，非印第安人占90%。那么现在我们就来讨论一下假如你的民调结果也存在10%的误差，那你的样本数据收集必须差到什么地步。有两种情况都可以造成这种误差。第一种，你没有发现任何印第安人，认为100%的人都是非印第安人；第二种，你发现有20%的人口是印第安人，非印第安人占80%。在第一种情况下，你漏掉了生活在该州的全部印第安人；在第二种情况下，你在计算印第安人数量时多计算了整整一倍。无论是哪种情况，都是极其严重的抽样错误，你的计算结果均偏离了100%：[（0–10）/10]以及[（20–10）/10]。但是，如果你只是错误地计算了20%的印第安人—与第一项共和党民主党人数调查的错误程度一样，则你的结果将会是8%的印第安人和92%的非印第安人，跟该州的真实人口情况只相差20%。

当p与1–p接近50%时，相对小的抽样错误在民调结果中就会被放大为严重的绝对错误。而当p或者1–p 接近于零时，就会出现相反的现象：即使是相对严重的抽样错误反映在民调结果中，也会变得微不足道。

同样是20%的抽样错误，在民主党和共和党人数调查中导致结果出现10%的误差，但在印第安人口的调查中却只有2%的误差。由于民意测验中的标准误差是以绝对值的形式表达的（例如±5%），计算公式决定了这一误差在p和1– p接近50%时达到最大。