中心极限定理的核心要义介绍

Naked Statistics

一辆坐满肥胖乘客的抛锚客车停在你家附近的路上，你推断一下，它的目的地是马拉松比赛场地，还是国际香肠节展厅？

有时候统计学就像魔术一样，能够从少量数据中得出不可思议的强大结论。我们只需要对1 000个美国人进行电话调查，就能洞悉美国总统大选的得票数；我们通过对一家禽肉加工厂生产的100块鸡胸肉进行沙门氏菌检测，就能得出这家工厂的所有肉类产品是否安全的结论。这些“一概而论”的强大能力，到底是从哪里来的？

绝大部分来自中心极限定理，或者说统计学界的勒布朗·詹姆斯，勒布朗同时还是超级模特、哈佛大学教授和诺贝尔和平奖获得者。中心极限定理是许多统计活动的“动力源泉”，这些活动存在着一个共同的特点，那就是使用样本对一个更大的数量对象进行推理（比如民意调查或是沙门氏菌检测）。这类推理看上去似乎充满神秘感，但事实上，它们只是我们已经探讨过的两个工具相结合的产物，这两个工具是概率和抽样调查。在开始对中心极限定理的工作机制进行介绍之前（其实也没有那么难以理解），我们先来看一个例子，让大家有一个大致感受。

假设你所生活的城市正在举办一场马拉松比赛。来自世界各国的运动员们齐聚一堂，准备一决高下，但他们中的许多人都不会说英语。按照比赛组委会的安排，每位运动员在比赛当天的早上签到之后，会被随机分配到一辆驶往起点的长途客车。不凑巧的是，其中的一辆长途客车没有按规定到达比赛现场，为了省去大量额外的运算，我们假设这辆客车上没有一个人有手机，而且车里也没有装载全球定位系统（GPS）设备。作为市民中的一员，你加入了搜寻长途客车的队伍。

偏偏就那么巧，在你家附近有一辆抛锚的长途客车，车上坐着一大群面露不快的国际乘客，他们中没有一个人会说英语。这肯定就是那辆失踪的车，你将会成为这座城市的英雄！但就在此时，一个疑惑出现在你的脑中：这辆车上的乘客看上去都“不瘦”，准确地说，他们都很胖。粗略扫一眼这些人，你估计这些乘客的平均体重至少有220磅（100公斤）。随机分配的马拉松运动员的体重不可能这么重，你打开对讲机对搜寻总部汇报道：“不是这辆客车，请继续搜寻。”

进一步的调查证实了你最初的判断是正确的。赶到现场的翻译人员经过一番交流后，你终于知道这辆抛锚的客车原本是要前往国际香肠节会场的，正好这一届的香肠节也在这座城市举办，连日期都碰巧相同。而且从视觉角度考虑，参加香肠节的人完全有可能也穿着宽松的运动长裤。

祝贺你！如果你能够体会上述的推理过程，也就是说，通过快速观察车上乘客的体型来判断他们并非马拉松运动员，那么你就已经领会了中心极限定理的基本理念，剩下的工作就是在这个基本框架下充实细节了。一旦你理解了中心极限定理，统计推断的绝大多数形式将会变得非常直观。

中心极限定理的核心要义就是，一个大型样本的正确抽样与其所代表的群体存在相似关系。当然，每个样本之间肯定会存在差异（比如前往马拉松起点的这么多辆客车，每辆客车乘客的组成都不可能完全相同），但是任一样本与整体之间存在巨大差异的概率是较低的。正是因为这个逻辑，让你对那辆载满肥胖乘客的抛锚客车做出了快速判断。的确有胖人参加马拉松比赛，每一次马拉松比赛中都会有几百名参赛者的体重在200磅以上，但绝大多数的马拉松运动员还是比较瘦的。因此，如此之多的“重量级”运动员被随机安排到同一辆客车上的概率可以说是很低的，所以你完全有理由认为这不是那辆失踪的马拉松客车。当然，有可能你的判断是错的，但概率告诉我们你更有可能是对的。

这就是中心极限定理背后的基本经验。如果我们再附加一些统计学工具，就能将正确或错误的可能性进行量化。例如，在一场有10 000名选手参加的马拉松比赛中，运动员的平均体重为155磅，我们可以算出，一个包含60名选手（也就是一辆客车的载客量）的随机样本的平均体重大于或等于220磅的概率不足1/100。但在此刻，让我们还是从直觉出发进行计算。通过运用中心极限定理，我们能够得出如下推理，这些推理都将会在下一章里进行深入阐述。

1.如果我们掌握了某个群体的具体信息，就能推理出从这个群体中正确抽取的随机样本的情况。举个例子，假设某学校的校长手里有本校所有学生的统考成绩（平均分、标准差等），这就相当于一个相关人口数据，再过一个星期的时间，区领导将会来学校随机抽取100名学生进行一次类似统考的测验，这100名学生的成绩—也就是一个样本，将会作为考核该校教学质量的指标。

随机抽取的这100名学生的考试成绩是否能够准确地反映出全校学生的平均水平呢？校长需要为此担心吗？根据中心极限定理，这100名学生作为一个随机样本，其平均成绩不会与全校学生的平均成绩产生较大差异。

2.如果我们掌握了某个正确抽取的样本的具体信息（平均数和标准差），就能对其所代表的群体做出令人惊讶的精确推理。从定理的使用角度来看，这与上一点内容正好相反。还是以上述假设为例，如果你是区领导，想要对本区域内的各个学校进行教学质量考核，与校长不同的是，你手中并没有（或不信任）某所学校所有学生的统考成绩，因此就有必要对每所学校进行抽样测试，也就是随机抽取100名学生参加一场类似统考的测验。

作为主管教育的领导，你觉得仅参考100名学生的成绩就对整所学校的教学质量做出判断是可行的吗？答案是可行的。中心极限定理告诉我们，一个正确抽取的样本不会与其所代表的群体产生较大差异，也就是说，样本结果（随机抽取的100名学生的考试成绩）能够很好地体现整个群体的情况（某所学校全体学生的测试表现）。当然，这也是民意测验的运行机制所在。通过一套完善的样本抽取方案所选取的1 200名美国人能够在很大程度上告诉我们整个国家的人民此刻正在想什么。

请跟上我的节奏：如果上面的第一点内容是成立的，那么第二点内容一定也成立，反之亦然。如果抽取的每一个样本与其所代表的群体确实存在相似关系，那么这个群体将总是与其样本保持一致性。（如果孩子与其父母长得很像，那么父母肯定也与孩子长得很像。）

3.如果我们掌握了某个样本的数据，以及某个群体的数据，就能推理出该样本是否就是该群体的样本之一。这就是我们在本章一开始的时候所举的那个马拉松比赛失踪客车的例子。已知马拉松参赛选手的平均体重（估算），以及那辆抛锚客车上所有乘客的平均体重（目测），通过中心极限定理，我们就能计算出某个样本（客车上的肥胖乘客）属于某个群体（马拉松比赛选手）的概率是多少，如果概率非常低，那么我们就能自信满满地说该样本不属于该群体（例如，客车上的乘客看上去真的不像是一群前往马拉松比赛起点的运动员）。

4.最后，如果我们已知两个样本的基本特性，就能推理出这两个样本是否取自同一个群体。让我们回到那个（越来越荒谬的）客车的例子上。我们现在得知这座城市即将同时举办马拉松比赛和国际香肠节，假设这两个盛会都将会迎来数以千计的参与者，而且他们都乘坐主办方安排的客车前往会场，因此客车上要么是随机安排的马拉松运动员，要么是随机安排的香肠爱好者。进一步假设有两辆客车在路上撞在一起了（我已经承认这是一个荒谬的例子，所以还请诸位读者勉强读下去吧），作为这座城市的管理者，你被派往现场了解事故情况，看看这两辆客车是不是都前往同一个地点（马拉松比赛或香肠节）。让人不可思议的是，两辆客车上的乘客都不会说英语，但到场的医护人员给你提供了一份关于这两辆车上的乘客体重的详细信息。

仅从这一点信息，你就能推理出这两辆客车前往的是相同的会场还是不同的会场。请再次用你的直觉进行判断，假设其中一辆客车上乘客的平均体重为157磅，标准差为11磅（也就是说绝大部分乘客的体重为146～168磅）。而另一辆客车上乘客的平均体重为211磅，标准差为21磅（即绝大部分乘客的体重为190～232磅）。此刻请忘掉所有的统计学公式，仅凭逻辑做出判断：这两辆客车上的乘客是从同一个群体中随机抽取的样本吗？

不是。一个更有可能的情形是：其中一辆客车上是马拉松运动员，而另一辆客车上则是香肠爱好者。除了平均体重的不同以外，想必你还注意到了两辆客车乘客之间的体重差异要远大于各客车内部乘客的体重差异，总重量较轻的客车里高于平均值一个标准差的乘客体重（168磅），但还是轻于另一辆客车上低于平均值一个标准差的乘客体重（190磅），这一点表明（无论从统计学的角度还是从逻辑的角度）这两个样本有可能来自不同的群体。

如果凭借直觉能理解到这一步的话，就说明你已经理解了93.2%的中心极限定理了。我们需要更进一步，在直觉背后加上一些技术支撑。显而易见，当你登上一辆抛锚的客车，发现里面坐满了身穿宽松运动裤的“肥胖”乘客时，你的直觉会告诉你他们不会是马拉松运动员。而中心极限定理能够让你在直觉的基础上更上一层楼，为你的判断提供数据支持。

举个例子，通过一些基本的运算，我们能够得出结论，在99%的情况下，任何一辆随机安排的客车上的选手的平均体重，都将会在全体运动员平均体重±9磅的范围之内。这就是当我偶遇一辆抛锚客车时做出上述判断的统计学支持。这些乘客的平均体重高于全体马拉松运动员平均体重整整21磅，只有低于1%的概率是马拉松运动员。因此，我可以有99%的把握认为这不是那辆失踪的马拉松客车，也就是说，我可以预期我的推理有99%的胜算。

当然，依照概率，我的推理中有1%的概率是错的。

这类分析全都源自中心极限定理。从统计学的角度看，该定理拥有和勒布朗·詹姆斯一样强大的威力和优雅品质。根据中心极限定理，任意一个群体的样本平均值都会围绕在该群体的整体平均值周围，并且呈正态分布。没有理解这句话？别着急，让我将这句话拆开来慢慢为大家解释。

1.假设有一个群体，如之前提到的马拉松比赛，我们对参赛运动员的体重感兴趣。将所有随机抽取的运动员体重样本（如某辆客车上的60名运动员）求平均值。

2.我们将样本抽取的工作重复再三，如不断地在运动场上随机抽取60名运动员，并将每组样本的平均体重记录下来。

3.这些样本平均值中的绝大部分都极为接近所有运动员的平均体重。有一些会稍高一点，有一些会稍低一点，只有极少数的样本平均值大大高于或低于群体平均值。

现在可以放背景音乐了，因为接下来就是奇迹发生的时刻……

4.中心极限定理告诉我们，这些样本平均值会在群体平均值周围呈现一个正态分布。我想大家应该还记得本书第2章里介绍的正态分布，也就是一条形似“铁钟”的曲线，有68%的数值位于平均值一个标准差的范围之内，95%的数值在平均值两个标准差的范围内，以此类推。

5.不论所研究的群体是怎样分布的，上述结论始终都是成立的。就算样本所在的群体不是正态分布，也不影响其样本平均值的正态分布形态。

让我们用一些真实的数据来说话，以美国的家庭收入分布为例。在美国，家庭收入并不是呈正态分布的，而是具有向右偏移的趋势。在某个年份里，没有一个家庭的收入会是负数，因此零美元就是分布曲线的最小值。与此同时，还有小部分家庭的收入会高得离谱儿，达到数百万美元甚至数十亿美元，因此我们可以想象分布曲线的右侧将会有一条长长的“尾巴”，如同9–1所示。

图9–1　美国家庭年收入分布

美国所有家庭收入的中位数大约为5.19万美元，平均数为7.09万美元。（像比尔·盖茨这类富豪使得家庭收入的平均值向右移动，这跟他在第2章走进酒吧的例子是同一个道理）。现在假设我们随机抽样1 000个美国家庭并询问他们的年收入，根据已知的信息，从中心极限定理出发，我们能对这个样本作怎样的推理？

其实结论有很多。首先，我们最应该得出的推理是，任何一个样本的平均值将会约等于其所在群体的平均值。样本的作用就是代表其所在的群体，也就是说，该样本要相似于其所在的群体。从大体上看，一个正确抽取的家庭样本应该能够反映美国所有家庭的情况，里面会包含基金经理、无家可归者、警察以及其他人，这些人出现的频率与他们在人口构成中的占比相关。因此，我们能够推测，这个包含1 000个美国家庭代表性样本的家庭年收入的平均值约为7.09万美元。这个数字准确吗？并不准确，但也不会差得太多。

如果我们进行多次类似的抽样调查，就会发现这些不同样本的平均值基本上都接近于群体平均值—7.09万美元。我们还可以推测，有一些样本的平均值要高一点，一些样本的平均值要低一点，那么我们有可能得到一个42.7万美元的样本平均值吗？当然可能，但是概率非常低。（要注意的前提是，我们的取样方法是完善可靠的，我们不会在如格林尼治乡村俱乐部这类富人聚集地的停车场里进行抽样）。同理，如果进行了正确抽样，那么得到一个仅为8 000美元的样本平均值的概率也是非常低的。

这些都只是基本逻辑。中心极限定理通过对不同样本平均值出现概率的描述，能够让我们推理出更为深入的结论。在这个例子中，样本平均值将会围绕着群体平均值（也就是7.09万美元）形成一条正态分布曲线。记住，群体本身的分布形态并不重要，美国家庭收入的分布曲线并非正态分布，但样本平均值的分布曲线却是正态分布。如果我们连续抽取100次包含1 000个家庭的样本，并将它们的平均值的出现频率在坐标轴上标出，那么我们基本可以确定在7.09万美元周围将会呈现一个熟悉的“铁钟”曲线分布。

取样次数越多，结果就越接近正态分布；而且样本数量越大，分布就越接近正态分布。为了检验这一结论，我们可以进行一项有趣的实验，研究对象是美国人的真实体重。密歇根大学主持了一项名为“变化的一生”的纵向研究，对几千名美国成人的各项指标进行了监测，其中就包括他们的体重。体重分布曲线稍微右偏，这是因为从生理学的角度解释，成年人超过正常体重100磅总是要比低于正常体重100磅更容易。这项研究中包含的所有成年人的平均体重为162磅。

通过使用最基础的统计软件，我们可以让电脑从“变化的一生”数据库中随机选取100名成年人组成样本，事实上，如果我们不断重复这一操作，就可以验证其结果是否符合中心极限定理的预测。下图为“变化的一生”数据库中随机生成的100个样本的体重平均数（四舍五入到磅）的分布情况。(www.xing528.com)

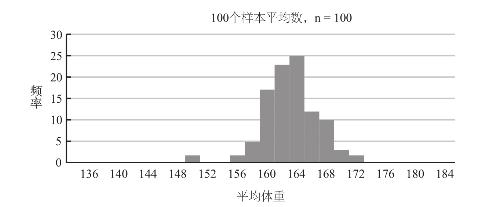
图9–2　样本平均体重公布图

样本数量越大，取样次数越多，样本平均值的分布就越接近一条正态分布曲线。（有一个经验是，样本数量必须达到30，中心极限定理才能保证成立）。这不难理解，样本所包含的数量越多，其平均值就越不容易受到随机偏差的干扰。如果一个样本只有两个人，那么其平均值就极有可能受到某一个体重特别重或特别轻的人的影响；与之相反，假如一个样本里有500人，那么即使里面有一些体重异常的人，总体的平均值也不会差得太多。

我们梦想着有朝一日能够用统计学解决所有的问题。现在，我们距离梦想成真只有一步之遥！上文已经提到，样本平均值基本呈正态分布，而正态分布曲线的过人之处就在于，我们能够大体确定有多少比例的数值位于整体平均值的一个标准差之内（68%），有多少数值位于两个标准差之内（95%），以此类推。这就是我们的“撒手锏”。

本章开头部分指出，我们可以凭直觉判断一辆客车载满乘客的平均体重比全体马拉松运动员的平均体重高25磅，那么这辆客车很可能不是那辆大赛组委会正在寻找的客车。为了将这一直觉量化，也就是说上述判断的正确率为95%、99% 或99.9%，我们只需要再获得一个技术参数就可以了，那就是标准误差。

标准误差被用来衡量样本平均值的离散性。我们如何评价样本平均值在群体平均值周围的聚集程度？为了避免混淆，我们首先需要对两个概念进行区分：标准差和标准误差。关于这两个概念，我们有必要记住的是：

1.标准差是用来衡量群体中所有个体的离散性。在之前的例子中，标准差衡量的是弗雷明汉心脏研究中所有参与者的体重分布，或马拉松比赛中所有参赛运动员的体重分布。

2.标准误差衡量的仅仅是样本平均值的离散性。如果我们反复从弗雷明汉心脏研究数据库中抽取100名参与者作为样本，并计算其平均值，那么这些样本平均值的分布会是怎样一种情况？

3.现在就是将这两个概念合二为一的时刻：标准误差就是所有样本平均值的标准差！这个结论是不是很酷？

如果标准误差差很大，就意味着样本平均值在群体平均值周围分布得极为分散；如果标准误差差很小，就意味着样本平均值之间的聚集程度很高。下面是取自“变化的一生”数据库的3个真实案例。

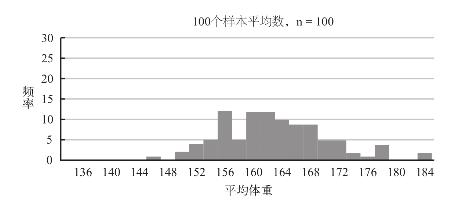
图9–3　样本平均值分布图（n=20）

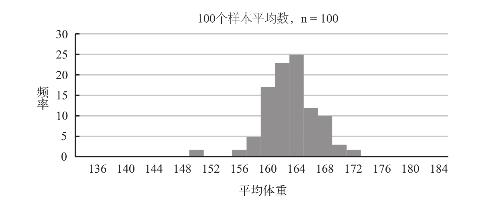
图9–4　样本平均值分布图（n=100）

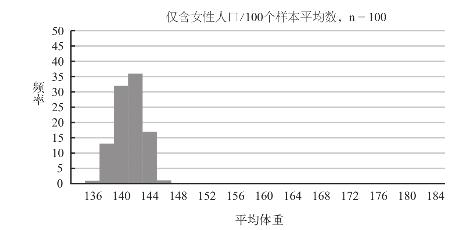
图9–5　女性样本平均值分布图

第二张分布图的样本数量较大，因此与第一张图相比，其平均值分布要更为密集一些，也更加靠近整体平均值，这是因为样本数量越多，其平均值就越不容易偏离整体平均值。最后一张分布图所描绘的仅仅是研究对象里的一个分支—女性人口，由于数据库中的女性人口体重分布相比起整体人口来说要更为紧密，因此从图中我们也不难看出，样本平均体重的离散程度要小于整个“变化的一生”数据库。（这些样本所在的整体人口的体重平均值实际上也有细微差别，这是因为“变化的一生”数据库里女性参与者的平均体重与全体参与者的平均体重是不同的。）

上述结论在一般情况下都是成立的。样本平均值的聚集程度会随着样本数量的增多而上升（例如，样本数量为100的分布图看上去就要比样本数量为30的紧凑）。所在群体人口的数据分布越分散，那么其样本平均值的聚集程度就越低。（例如，整个“变化的一生”数据库样本平均值的离散程度就要高于单纯的女性人口。）

如果到目前为止你都能够理解，那么接下来的这个计算标准误差的方程式应该不会成为难点：

SE = 其中SE表示标准误差，s表示抽样群体的标准差，n表示样本的 数量。请随时保持头脑清醒！千万不要让表面的字母干扰你的直觉判断。如果标准差本身的数值很大，那么标准误差的数值也不会小。取自一个高度离散群体的大规模样本，其离散程度也会很高；与之对应，如果是一个高度聚集的群体，其样本围绕平均值的聚集程度也会很高。如果还是以体重为例，我们可以推测，取样自“变化的一生”全体人口的标准误差会大于仅取样自其中20～30岁男性人口的标准误差。这也是为什么公式中的标准差（s）出现在分子的位置上。

同样的，如果样本数量变大，那么标准误差就会变小，这是因为大型样本受极端异常值的影响相对较小。这也是为什么公式中的样本数量（n）出现在分母的位置上（至于为什么要对样本数量n开根号，我们就留给更高阶的书籍去解释吧，在这里我们只需要理解最基本，也是最重要的关系）。

在“变化的一生”的例子中，我们知道整体人口的标准差，而实际上这一点通常是很难做到的。对于大型样本来说，我们可以认为样本的标准差接近于整体人口的标准差。

经过刚刚这一场头脑风暴，我们终于等到了品尝胜利果实的时刻。由于样本平均值是呈正态分布的（这一点要归功于中心极限定理），我们便可以通过这条神奇的曲线来获得推理所需的“超能力”。已知的是，差不多有68%的样本平均值会在群体平均值一个标准误差的范围之内，有95%的样本平均值会在群体平均值的两个标准误差的范围之内，有99.7%的样本平均值会在群体平均值3个标准误差的范围之内。

图9–6　样本平均值概率分布图

现在让我们回到对失踪客车案例的思考中（但这个例子还将会延续其“荒诞”的特点，我保证下一章会引用更多真实、合理的案例），这次我们需要用数字来代替直觉。假设“变化的一生”研究小组邀请了所有参与者前往波士顿共度周末，并在这期间进行一次完整的数据采集工作。参与者被随机分配到每一辆客车上，来往于不同的设备进行称重、验血等检测。令人意外的是，其中有一辆客车失踪了，当地新闻还特地报道了此事。与此同时，你正从国际香肠节的活动现场赶往这里，因为你刚刚处理了一起交通事故，一辆客车为了躲避一只野生狐狸冲到了马路外边，客车上所有的乘客都失去了意识，但所幸伤得不重（这个例子需要他们失去交流能力，但我个人又不想使他们伤势过重，于是只能出此下策）。医护人员告诉你那辆客车上所有62名乘客的平均体重为194磅，此外，客车想要竭力躲闪的狐狸也受伤了，一条后肢看上去似乎骨折了。

幸运的是，你恰好知道“变化的一生”数据库上所有参与者的平均体重和标准差，而且你也知道中心极限定理的工作原理，最重要的是，你还知道如何给一头野生狐狸急救。“变化的一生”研究的参与者的平均体重为162磅，标准差是36，在此基础上，我们能够计算得出一个数量为62人（也就是客车上正处于昏迷中的那些乘客）的样本的标准误差为：s/= 36/7.9，即4.6。

样本平均体重（194磅）与整体平均体重（162磅）之间有32磅的差距，是标准误差的3倍多。我们从中心极限定理得知，99.7%的样本平均值会处于整体人口平均值3个标准误差的范围内，因此出事的那辆客车上搭载的是“变化的一生”项目的研究对象的概率几乎为零。作为这座文明城市的一分子，你有义务呼叫研究中心，告诉相关人员这很有可能不是他们所要找的那辆客车，而且除了告诉他们你的“直觉”以外，你还可以用统计数据来支撑你的判断。你在电话里可以这样说，你有99.7%的把握认定这辆客车不是他们正在寻找的那辆，由于电话那边听你说话的都是研究人员，他们肯定能够理解这个数字背后的含义。

在医护人员对客车上昏迷的乘客进行验血之后，你的分析得到了进一步的证实。这些乘客血液中的胆固醇含量的平均值比“变化的一生”项目的研究对象的平均值高出了5个标准误差，这些昏迷不醒的乘客事后被证明是国际香肠节邀请的嘉宾。

这个故事还有一个皆大欢喜的结局。在客车上的乘客们恢复了知觉以后，“变化的一生”研究组的科学家们为他们举办了一次名为“高饱和脂肪饮食的危害”的讲座，促使他们中的许多人逐渐养成了比以前更为健康的饮食习惯。与此同时，那只受伤的狐狸也在当地一家野生动物保护中心得到了悉心照料并痊愈了，最终健康地回归大自然。^[1]

本章自始至终讲的都是最基本的知识。大家要引起注意的是，为了能够让中心极限定理成立，样本数量必须足够多（依照经验法则，至少有30个）；如果我们想要假设群体的标准差等同于样本的标准差，那么更要保证样本数量足够多了。当这些情况都无法满足时，我们还有多种多样的统计学方法来弥补，但这些都是蛋糕上的装饰（甚至仅仅是蛋糕上的糖霜）。本章所介绍的“真家伙”才是既简单又实用的：

1.如果你从某个研究群体中多次随机抽取数量足够多的样本，那么这些样本的平均值会以整体平均值为中心呈现正态分布（不论该群体自身的分布情况是怎样的）。

2.绝大多数的样本平均值都会紧紧围绕在整体平均值的周围，通过计算标准误差就可以知道这些样本平均值到底是离得“近”还是“远”。

3.通过中心极限定理，我们便可知道样本平均值与整体平均值之间的距离及其概率。样本平均值离整体平均值两个标准误差的概率相对较低，3个或以上标准误差的概率基本上为零。

4.如果出现了某个概率较低的结果，我们便可以推测是不是有一些其他因素介入，而且概率越低，其他因素介入的可能性就越大。

这些基本上囊括了统计推断的所有内容，而中心极限定理是让这一切发生的重要推动力。只要勒布朗·詹姆斯的NBA总冠军戒指的数量没有超过迈克尔·乔丹（6枚），中心极限定理的魅力就将始终在乔丹之上。

【注释】

[1]我在芝加哥大学的一位同事吉姆·萨累就失踪客车的这个例子提出了一个非常重要的观点，他认为客车失踪的可能性通常很小，因此如果在我们寻找失踪客车的过程中，恰巧有一辆客车出事被发现了，就非常有可能是那辆失踪的客车，不管客车上的乘客到底有多重。我不得不承认，他说得对。（设想一下：如果你在逛超市时跟你的孩子走散了，而恰好在这个时候超市经理告诉你在6号收银台旁站着一位找不到父母的小孩，那么你基本上就能确定，那应该是你的孩子。）因此，我们还需要给这个例子加上一个更加荒谬的前提，那就是在这座城市总是有客车失踪。