概率与期望值：盲品选择米切罗与施利茨的概率

Naked Statistics

买福利彩票，去赌场豪赌、投资股票或期货，哪种方式让你跻身《福布斯》富豪排行榜的可能性更大？

1981年，美国约瑟夫·施利茨酿酒公司斥170万美元巨资为该公司旗下的旗舰品牌—施利茨啤酒开展了一场大胆而冒险的市场营销活动。当美国橄榄球超级杯大赛（即“超级碗”）的中场休息时间一到，施利茨公司就会当着全球亿万电视观众的面，现场直播一场别开生面的啤酒品鉴会，而挑选的对手不是别人，正是施利茨的死对头—米切罗啤酒，更让人大跌眼镜的是，参加品鉴会的不是别人，正是100名米切罗啤酒的忠实用户。这样的广告从始至终出现在季后赛的每一场比赛当中。类似的电视直播啤酒品鉴会总共有5场，每场都会邀请100名某品牌啤酒的“拥趸”，包括百威、米勒、米切罗等，让这些啤酒爱好者在自己最钟爱的啤酒和施利茨啤酒之间进行“盲品”。一边是如火如荼正在进行的职业橄榄球季后赛，一边是同样激烈的啤酒品鉴会，那时的广告标语甚至打出了“看季后赛，喝施利茨啤酒”的字样。

广告噱头很明确：即使是那些自认为喜欢另一种品牌的啤酒爱好者，在盲品时也会发现自己更偏爱施利茨啤酒。啤酒公司甚至还请了一位橄榄球职业联赛的前裁判来监督整个活动过程。考虑到在数量众多的电视观众面前举办这样一场充满风险的啤酒品鉴会，你肯定会觉得施利茨啤酒的口感一定特别好，否则哪会有勇气搞这样的宣传，是吗？

那可不一定。施利茨只需要生产出口感平平的啤酒，再掌握一些扎实的统计学知识，就能确保这项计谋肯定会成功—注意，我在写作时通常会非常谨慎地使用“计谋”这样的词，尤其是列举啤酒广告这样的例子。施利茨所生产的这种啤酒喝起来没什么特别的，跟绝大多数其他品牌的同类啤酒几乎没有太大差别；但讽刺的是，正是这一点成为施利茨啤酒广告营销的核心。可以假定的是，如果在街上随机找几个喜欢喝啤酒的人，他们基本上区分不出施利茨、百威、米切罗或米勒啤酒。因此，取其中任意两种品牌的啤酒进行盲品测试，猜对品牌的概率基本上和扔硬币差不多。大体来看，有1/2的人会选择施利茨，剩下1/2的人会选择“挑战”品牌的啤酒，单看这样的结果可能无法构成一个有说服力的广告营销（我们总不能说“既然口感都差不多，就选择施利茨吧”）。而且，施利茨啤酒公司绝对不会拿自己的忠实用户做试验，因为差不多有1/2的用户会“不小心”挑选其他品牌的啤酒。如果一群原本忠实于某品牌啤酒的消费者在盲品时竟然觉得竞争对手的啤酒好喝，这个品牌该有多悲哀啊，所以，施利茨就让这样的事情发生在其他品牌身上。

施利茨的高明之处在于，只邀请那些声称自己偏爱另外一个品牌啤酒的消费者参加测试。如果盲品的结果果真如抛硬币一样，那么就会有1/2的百威、米勒或米切罗啤酒的爱好者最终选择施利茨。这下施利茨扬眉吐气了，因为有1/2的百威啤酒爱好者更喜欢喝施利茨！

更妙的是，这一切都在橄榄球联盟决赛的中场进行直播，而且由一位身穿裁判服的橄榄球前裁判执法整个盲品过程。毕竟是电视直播，就算施利茨已经私底下进行了大量试验，并证明了有1/2的米切罗啤酒爱好者会选择施利茨啤酒，又有谁能够保证在最终直播的时候不出岔子？万一“超级碗”直播时选取的100名米切罗爱好者的味觉特别灵敏呢？虽然盲品测试在概率上等同于抛硬币，但万一就是有绝大部分人恰巧选择了米切罗呢？如果我们让100个人排成一队，逐个抛硬币，出现85或90个硬币反面向上的可能性也是完全存在的。对于施利茨公司来说，在直播时碰上这样的情况将会对它们的品牌造成毁灭性的打击（更不必说用于购买广告时段的那170万美元了）。

统计学的威力在这种时刻就体现出来了。如果这个世界上存在一个统计学领域的“超级英雄”，那么这时的画面就会是这个英雄俯身飞入施利茨公司总部，并向在场的高层揭开被统计学家称为二项分布（又名伯努利试验）的奥秘。二项分布的主要特点有，试验次数是固定的（例如100位啤酒盲品者），每一次试验都有两个可能的结果（施利茨或米切罗），而且每一次“成功”的概率都是相等的（假设选择任意一个品牌啤酒的概率为50%，如果选择施利茨的概率高就表示试验“成功”）。我们同时还假定所有的试验都是各自独立的，即一位盲品者的决定不会影响其他人的选择。

有了这些信息，这位统计学的“超级英雄”就能计算出所有可能出现的不同结果的概率，如52人选择施利茨，另外48人选择米切罗，或者是31人选择施利茨，另外69人选择米切罗，这种情况发生的概率是多少。当然，对于我们这些不具备超级运算能力的凡人来说，借助一台电脑同样也可以办到。所有100位盲品者都选择米切罗的概率是1/1 267 650 600 228 229 401 496 703 205 376，这可能比这些人在中场休息时被陨石砸中的概率还低。重要的是，重复这些基本运算，能够让我们知道某个结果范围内的累积概率，如有不多于40位盲品者选择施利茨的概率是多少。这些数据足以让施利茨的市场营销人员松一口气。

让我们假设，要让施利茨公司满意，100位盲品者中至少要有40位选择施利茨啤酒。这是一个非常可观的数字，因为所有参加盲品直播的人都曾信誓旦旦地声明自己是米切罗的忠实用户。而要达到这样的效果，其实一点儿都不难。如果盲品会果真如抛硬币一样，那么运用概率学的基本知识，就能得出至少有40人选择施利茨的概率为98%，至少有45人选择施利茨的概率为86%。从理论上来看，这场电视营销活动其实并没有很大的风险。

那么，现实中的结果又如何呢？在1981年“超级碗”中场休息的现场，正好有50%的米切罗啤酒的消费者在盲品测试中选择施利茨，不多不少，正好1/2。

从这个例子中，我们可以得到两个重要的启示：第一，概率是一个非常强大的统计学工具；第二，20世纪80年代的许多畅销品牌的啤酒确实在口感上没有什么区别。本章将主要就第一个启示展开叙述。

概率学是一门研究不确定事件和结果的学问。投资股市存在着不确定性，抛硬币同样也存在着不确定性，因为有的时候你得到的是硬币的正面，有的时候是硬币的反面。连续4次抛一枚硬币更是增加了这种不确定性，因为每一次都有可能是正面或反面，如果你手里有一枚硬币并且连续抛了4次，我事先无从得知4次的准确结果（你也不能），但我可以事先告诉你一些结果（如两个正面、两个反面）出现的概率要大于另一些（如4个正面）。从施利茨的例子里我们已经看到，像这类基于概率推导出来的结论会发挥意想不到的作用。事实上，如果你弄清楚了为什么连续4次抛同一枚标准硬币结果是正面的概率为1/16，那么你（再稍微做一点功课）就能理解生活中那些与概率相关的现象，从保险业的运作原理到橄榄球队的排兵布阵和赛场取舍。

我们先从简单的部分开始讲起。许多事件的概率是明确的，如抛一枚标准硬币结果是正面的概率为1/2，掷一粒骰子得到1点的概率为1/6，还有一些事件的概率能够从过去的数据中推导出来。在美国职业橄榄球比赛中，触地得分后踢定位球再得一分的平均概率为0.94，也就是说，每100个定位球中有94个会成功。当然，这一数据会随着不同球员、不同天气环境以及其他因素的改变而有所不同，但不会发生剧烈变化。在获得并信任此类信息的前提下，决策者常常能够看清风险、作出决定。举个例子，澳大利亚运输安全局发布了一份有关乘坐不同交通工具致死风险的量化报告，大家都觉得飞行非常可怕，但实际上商业航空旅行的风险是微乎其微的。澳大利亚自20世纪60年代起就再没有发生过一起商业航空致死事故，因此航空旅行每一亿公里的致死率基本为0。汽车每一亿公里旅行的致死率为0.5，真正吓人的是摩托车的致死率，如果你立志成为一名器官捐献者，那么你就选择摩托车出行吧，因为摩托车的致死率比汽车整整高出35倍。

2011年9月，美国航空航天局的一颗重达6.5吨的卫星退役，预计在进入地球大气层后开始分解。那地球上的人被卫星残骸砸中的概率有多大呢？我们是不是应该让孩子们待在家中不去上学？据美国航空航天局的一名火箭科学家计算，任何一个人被坠落的卫星残骸砸到的概率是21万亿分之一。要知道，在地球上任何一个角落不幸被车撞到的概率可是3 200分之一。最终，卫星在坠落地球的过程中解体，科学家们无法确认所有碎片的具体位置，当然，也没有出现任何人员伤亡的报告。概率并不会确凿地告诉我们将会发生什么，但我们通过概率计算能够知道很有可能发生什么、不太可能发生什么。聪明的人会使用这类数据为自己的事业和生活指明方向，比如说当你从广播里得知将要有一颗卫星坠落时，不会骑上一台摩托车全速开回家提醒家人不要出门。

当涉及风险的问题时，恐惧会让我们忽视数字背后的真相，反而对那些真正的危险视而不见。在史蒂芬·列维特和史蒂芬·都伯纳所著的《魔鬼经济学》一书中，提到了一个惊人的发现，那就是后院的游泳池远比柜子里的枪来得危险。列维特和都伯纳计算，10岁以下的儿童在游泳池溺死的概率要比枪击事故中意外中弹身亡的概率高100倍。康奈尔大学的3位研究人员嘉瑞克·布雷拉克、维琳达·卡地亚丽和丹尼尔·西蒙在一篇引人入胜的论文中这样说道，可能有数以千计的美国人在“9·11”恐怖袭击事件发生之后由于害怕坐飞机而死于非命。我们永远都不知道遭受恐怖袭击的真正风险到底有多大，但我们知道开车确实是一件危险的事。在“9·11”恐怖袭击事件发生之后，越来越多的美国人选择自驾出行，而不选择乘坐飞机。据统计，在考虑平均死亡率和天气等导致路面交通事故因素的前提下，2001年10～12月，平均每个月因交通事故致死的人数比以往多了344人。该效应随着时间的推移逐渐减弱，这是因为大家对恐怖主义的恐惧在慢慢消退，但这项研究的作者认为，“9·11”恐怖袭击事件导致的驾车死亡人数或已超过2 000人。

概率有时候还可以在事后告诉我们，什么情况是最有可能发生的，而什么情况是最没有可能发生的，比如DNA分析。电视剧《犯罪现场调查：迈阿密》里有这样一个场景，技术人员在谋杀案现场附近收集到一个丢弃的苹果核，上面残留着唾液，当然唾液上不可能写着杀人凶手的名字，就算让一位英俊的技术员用最先进的显微镜也观察不出什么。但是，唾液（或头发、皮肤、骨头碎片等）里却能找到DNA片段，这里面包含着独一无二的基因信息—每个人的基因都是不同的（除非是共享相同DNA的同卵双胞胎）。如果医学专家证实DNA样本吻合，就说明检方的取证工作取得了重要进展，但这还远不是全部。是的，从犯罪现场收集回来的DNA样本必须与犯罪嫌疑人身上的DNA相匹配，但检方同时还必须证明这两个DNA样本相吻合不是一个巧合。

人类的DNA序列中有很多片段是相同的，就像我们中有很多人拥有相同的鞋码、相同的身高、相同颜色的眼睛，事实上我们的DNA序列中有超过99%的片段都是完全一样的。如果研究人员只能获得一小部分DNA样本，那么这上面的基因数量也是有限的，很有可能有数百万人的基因片段与实验室中的这部分DNA样本完全吻合。因此，基因数量越多，上面的自然遗传变异也就越多，取证的准确率也就越高。换言之，DNA样本与多个人的DNA相吻合的概率也就越低。

不知道大家是否看明白了。让我们来想象一下，假设你的“DNA数据”由你的手机和社保号码组成，这19个数字组成了独一无二的你。每一个数字都代表一个有10种变化可能的基因：0、1、2、3等。如果在犯罪现场，调查人员发现的“DNA数据”残留片段为：_ _ 4 5 9 _ _ _ 4 _ 0 _ 9 8 1 7 _ _ _，而且正好与你的“DNA数据”相吻合。你认罪吗？

你应该明确3件事。首先，除非是全部19个数字都吻合，否则总会有不确定性存在；其次，数字发现得越多，不确定性就越少；最后，不要忽略背景和事件的来龙去脉。如果警察发现你的时候，你正在超速驾驶汽车逃离事故现场，而且口袋里还装着受害者的信用卡，那你的这个“DNA数据”尽管不能完全确定，但也足以说服检方将你绳之以法了。

在资源和时间都非常充分的情况下，研究人员会对DNA中的13个不同区域进行一一比对，两个人的DNA在所有13次比对中都吻合的概率是非常低的。“9·11”恐怖袭击事件发生以后，美国政府就是用DNA技术来核实遗体身份的。收集袭击现场找到的DNA样本，再与受害者家人提供的DNA样本进行比对，在这个过程中出现认错遗体的概率是10亿分之一，甚至更低。随着越来越多的遗体被识别并认领，剩下的遗体数量越来越少，出现混淆的概率也在下降，因此DNA比对的标准也逐渐放宽。

但在很多时候我们的资源是有限的，可能是收集到的DNA样本太小，也有可能是样本已经被污染，导致无法检测出全部13个基因片段，许多趣闻和争议由此引发。《洛杉矶时报》在2008年的时候连载了一组报道，讨论检方是否应该将DNA检测结果纳入刑事案件的举证范围内。该报特别提出了一项质疑，在法律实施过程中概率的使用是否低估了巧合的可能性，因为收集到全世界每一个人的DNA信息毕竟是不现实的，可以说美国联邦调查局和其他调查机构提交给法庭的DNA证据都是估计出来的概率。亚利桑那州一个犯罪实验室的分析员在测试本州DNA数据库时，发现两个没有血缘关系的重罪犯的DNA序列中的第9组基因相吻合，这一发现引发了轩然大波，因为根据美国联邦调查局的说法，无血缘关系的两个人第9组基因相吻合的概率仅为1 130亿分之一。在随后的调查中，其他州的DNA数据库也发现了第9组甚至更多组基因吻合的人，数量超过1 000对。这个问题将如何解决，还是留给法律执行机构及辩护律师去思考吧。我现在想说的是，头戴科技耀眼光环的DNA分析，归根结底仍然是一个概率问题。

很多时候，了解多重事件同时发生的概率是很有价值的。停电且备用发电机失灵的可能性有多大？两个独立事件同时发生的概率取决于这两个事件各自的概率，也就是说，事件A与事件B同时发生的概率是这两个事件发生概率的乘积。举个例子可能会更直观一些，抛一枚标准硬币得到正面朝上的概率为1/2，连续抛两次都得到正面朝上的概率为1/2×1/2 = 1/4，连续抛3次都得到正面朝上的概率为1/8，连续抛4次都得到正面朝上的概率为1/16，以此类推。同样，连续抛4次硬币都得到反面朝上的概率也应该为1/16。这也解释了为什么学校或办公室的电脑总会弹出一个对话框，提醒你提高开机密码的“安全级别”。假设你的开机密码为6位，而且用的全是数字，那么总共有10 × 10 × 10 × 10 × 10 × 10 = 106种数字排列组合，不要以为这种组合很复杂，对于计算机来说，不到一秒钟，就可以将这些数字排列组合全都试一遍。

所以，假设在你的系统管理员向你发表长篇大论之后，你终于同意将字母加入到密码设置的范围内，那样的话，6位密码就有了36种选择：26个字母加上10个数字。可能组合出的密码数量也上升到了36 × 36 × 36 × 36 × 36 × 36 = 366个，超过20亿个。如果系统要求将密码长度增加为8位，而且强烈建议你使用#、@、%、！等符号—芝加哥大学就是这样做的，那么可能组合出的密码数量便跃升至468，超过20万亿个。

有一点必须再次强调：这一公式只适用于相互独立的事件，也就是说，一个事件的发生及其结果对另一个事件不会造成任何影响。例如，你第一次抛硬币得到正面朝上的概率并不会影响你第二次抛硬币得到正面朝上的概率。相反的，今天下雨的概率与昨天是否下雨并不是相互孤立的，因为下雨作为一种天气现象具有连续性，有时候经常连续几天都下雨。同样的，你今年出车祸的概率与明年出车祸的概率也不是相互孤立的，今年导致你出车祸的原因很有可能也会导致你明年发生类似的车祸，比如你有可能经常酒后驾车、喜欢跟别人飙车、习惯开车时发短信，或者车技很差。这也是为什么你的车险费率会在发生车祸后上升，并不仅仅是因为保险公司想要从你这里挽回一点儿它们为你支付的赔偿金，更重要的是，它们拥有了关于你未来发生车祸概率的新信息—当你开车撞向你的车库大门之后，这个概率就上升了。

假如你对发生这个事件或发生那个事件的概率感兴趣，也就是出现结果A或出现结果B的概率（再次假设两个事件是相互独立的），这个概率就是A和B各自的概率之和：A概率 + B概率。举个例子，掷一次骰子得到1点、2点或3点的概率就是它们各自的概率之和：1⁄6 + 1⁄6 + 1⁄6 = 3⁄6 = 1/2。这个问题理解起来应该不难，掷骰子会得到6种可能的结果，点数1、2或3出现的概率占了所有出现概率的1/2，因此我们有50%的概率掷出1、2或3点。如果我们在拉斯韦加斯赌双骰，掷出7点或11点的概率就是两颗骰子点数相加为7或11的组合数除以总共可能出现的点数组合数，得到的答案是8/36。

通过概率的计算，我们还可以得到在所有管理决策的过程中，尤其是在金融领域是最实用的统计工具：期望值。期望值是基础概率学的升级版。某个事件如买彩票的期望值或收益，实际上就是所有不同结果的和，其中每个结果都是由各自的概率和收益相乘而来。跟往常一样，我们还是用例子来说明这个问题。假设你参与了一个掷骰子的游戏，游戏规则是掷出1点可以获得1美元，掷出2点可以获得2美元，掷出3点可以获得3美元，以此类推。那么在这个游戏中，掷一次骰子的期望值是多少？每一个结果都有1/6的概率，因此期望值为：

1⁄6 （1美元） + 1⁄6 （2美元） + 1⁄6 （3美元） + 1⁄6 （4美元） + 1⁄6 （5美元） + 1⁄6 （6美元） = 21⁄6，即3.5美元。

粗略看一下，3.5美元的期望值似乎是一个无效数据，毕竟你不可能掷一次骰子就获得3.5美元（因为所有收益都是整数）。但事实上，期望值是一个非常有用的参考数据，通过比较成本投入和期望收益，你就能知道做这件事是不是“值得”。如果在上述游戏中，每掷一次骰子需要缴纳3美元，你还玩吗？当然，因为期望回报（3.5美元）要高于游戏成本（3美元）。这虽然并不代表你第一次玩就保证能赚到钱，但至少可以帮助你认清哪些事情值得冒险。

在上面这个例子的基础上，我们可以进一步将期望值延伸到美国职业橄榄球领域。之前提到，在比赛中触地得分之后，球队将会面临两个选择，要么直接射门再得一分，要么进行一次两分投球的尝试。如果选择前者，则在三码线处定点踢球穿过球门柱即可；如果选择后者，则需要从三码线处将球带到或传到球门区把对方逼成死球，可以想象其难度之大。因此，球队可以选择简单的打法得1分，也可以选择难度高的打法得2分。应该怎么选？

统计学家或许不玩橄榄球，也从不和啦啦队队长约会，但他们却能够为球队教练提供指导。在前文中已经提到，触地后成功点射的概率为0.94，也就是说这一尝试的期望值为0.94，因为回报（1分）乘以成功概率（0.94）得到的结果为0.94分。没有队伍能在比赛中打出0.94分，但这个数字能够量化触地后的一种选择，从而与另一种选择—2分尝试进行直观的比较。2分尝试的期望值要低得多，才0.74分，虽然回报很高（2分），但成功率却低得可怜（0.37）。由此可见，如果比赛只剩下一秒钟的时间，一支队伍在触地得分后还落后对手2分，这支队伍别无选择，只能进行2分尝试；但如果某支队伍处于领先，其目标只是在比赛中扩大比分优势，那么就应该采取得1分策略。

运用与上述例子相同的基础性分析，我们还可以解释为什么永远不要买彩票。在伊利诺伊州，每张彩票的背面都印着不同玩法和等级的中奖概率，假如我买了一张1美元的即开型彩票，在彩票背面印着的细小文字里我可以找到不同等级奖金的中奖概率：1/10（1美元，即免费再来一张）、1/15（2美元）、1/42.86（4美元）、1/75（5美元），一直到概率为1/40 000的1 000美元。我将每一个等级的中奖概率乘以奖金额度，最后将得到的结果相加，计算出购买此类彩票的期望值。结果是这种1美元彩票的回报期望值约为0.56美元，所以这绝对是一项糟糕的投资。但我的运气还不错，中了2美元。

虽然我中了2美元，依然无法改变购买彩票是一种愚蠢行为的事实，这就是概率教给我们的重要经验之一。通过概率计算得出的好决策，有时会得到坏的结果；而坏的决策—如在伊利诺伊州购买1美元即开型彩票—有时还是会有好处，至少从短期来看是这样。但最终“笑傲江湖”的还是概率，因为谁也打败不了概率。有一个重要的定律叫作大数定律，即随着试验次数的增多，结果的平均值会越来越接近期望值。是的，我今天买彩票的确中了2美元，我明天也有可能再中2美元，但如果长年累月地买下去，每天买的都是这种预期回报为0.56美元的1美元即开型彩票，那么赔钱将是毋庸置疑的事，到了买齐100万张彩票的那一天（也就意味着我花了100万美元），我最终的中奖金额约为56万美元。

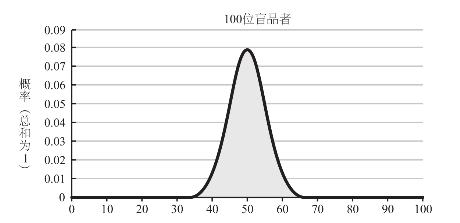
我们也可以用大数定律来解释为什么赌场从长期来看总是挣钱的问题。赌场内所有项目的概率都是有利于赌场老板的（出“老千”的赌客不考虑在内）。如果赌场的营业时间足够长，吸引的下注人数也足够多，那么赌场从赌桌赚到的钱肯定要比付出的要多。通过大数定律，我们还可以解释为什么施利茨要在“超级碗”中场休息时邀请100位而不是10位啤酒爱好者来参与啤酒盲品测试。下面是“施利茨型”测试的“概率密度函数”，测试人数分别为10、100和1 000。不要被这个函数的名称吓到，其实函数本身并不复杂，X轴罗列了各种可能出现的结果，Y轴表示的是对应结果出现的概率。需要在这里重申一遍的是：我们的前提是所有品牌啤酒的口感是差不多的，品尝选择的过程类似于扔硬币，每位盲品者选择施利茨的概率都为50%。我们可以从以下的3幅函数图中看到，随着盲品者人数的增多，越来越多的预期结果向中间（也就是有一半的人选择施利茨啤酒）集中；与此同时，位于曲线两端的极端结果出现的概率则下降得非常厉害。

图5–1　选择施利茨啤酒的盲品者人数

(www.xing528.com)

图5–2　选择施利茨啤酒的盲品者人数

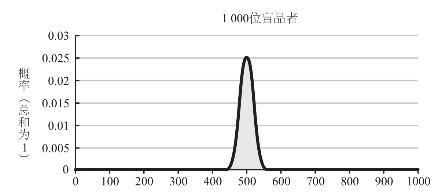
图5–3　选择施利茨啤酒的盲品者人数

在前文中我说过，如果有大于或等于40%的米切罗啤酒爱好者在盲品测试中选择了施利茨啤酒，那么施利茨的高层就满意了。下面就列举了不同盲品人数的条件下得到满意结果的概率：

10人：0.83。

100人：0.98。

1 000人：0.9 999 999 999。

1 000 000人：1。

读到这里，我想很多人已经能够领会“千万别为标价99美元的打印机购买保修延长服务”的含义了。整个保险行业都是建立在概率的基础之上，保修只不过是保险的一种表现形式而已。为某件东西上保险也就意味着与保险公司签订了合同，明确规定当某些意外发生时，投保人能够获得一定数额的赔付。例如，在你的汽车被盗或撞到树上之后，你就可以根据所购买的车险合同进行索赔。但在享受到这一项保障服务之前，你需要支付一笔费用，以换得一定期限的保障。对于保险公司来说，为了从你这里获得定期定额的保费，它们需要承担你的车被盗、撞毁，甚至因为你的差劲儿的驾驶技术而引起的各种车辆损坏风险。

为什么这些公司愿意承担这些风险？原因就在于，如果保险公司制定的保费标准正确合理，从长期来看将会给公司带来不菲的收益。好事达保险（财富500强公司之一）承保的车辆中肯定有一些会被盗，还有一些车会因车主驾车撞到消防栓而送进修理厂，我高中时的女朋友就遇到过这种情况，不仅她的车辆撞坏，她还要赔偿那个被撞坏的消防栓—贵到令人无语。但无论是好事达还是其他任何一家保险公司，它们承保的车辆中绝大部分都不会发生事故。为了挣到钱，保险公司只需要保证收取的保费多于付出的赔偿金就行了，为了做到这一点，公司必须清楚地知道合同里每一项条款可能会带来的赔偿金额，行业术语叫作“预期损失”。这和预期值是完全相同的概念，只不过是套上了保险的外衣。假设车的赔偿额度为4万美元，每年被盗的概率是1/1 000，那么该车的年预期损失为40美元，车险保费组成中盗窃险种的定价就应该高于40美元，这样看来，保险公司和赌场、伊利诺伊州彩票的性质是一样的，它们都需要付出，但从长期来看，得到的肯定要比付出的多。

作为消费者，你应该知道，从长远来看，保险并不能为你省钱。保险能为你做的是，当你遭遇一些难以承受的巨大损失时，如价值4万美元的汽车被盗、35万美元的房子被烧毁等，为你提供赔付，帮你渡过难关。从统计学的角度来看，购买保险是一项“糟糕的投资”，因为平均来看，你支付给保险公司的钱永远要比得到的赔付多。但如果想防止一些足以毁掉你生活的结果出现，保险就是一个理性的工具。讽刺的是，一些巨富如巴菲特倒是可以不用买车险、房屋险，甚至医疗保险，从而省下不少钱，因为就算有再糟糕的事情发生在他的身上，他都能承担得起。

最后，我们来说说你那价值99美元的打印机。假设你刚刚从百思买或其他地方精挑细选了一台好评如潮的激光打印机。当你结账的时候，销售人员会向你提供一份详细的保修延长清单，比如说额外支付25美元，可以延长一年的免费修理或更换服务，支付50美元可以延长维修服务两年。现在你对概率、保险以及基础经济学已经有了一些基本的了解，你可以很快联想到以下几点：（1）百思买是一个以赢利为目的的商家，因此追求利润最大化是它不变的追求；（2）销售助理正在竭尽所能地劝你购买保修延长服务；（3）从前两点能够推测出，购买保修延长服务的代价要高于商家为你修理或更换打印机的预期成本，如果不是这样，那么商家就不可能会如此卖力地推销了；（4）就算价值99美元的打印机坏了，你需要自掏腰包来修理或换一台新机器，也不会给你的生活造成太大的困扰。

一般来说，你为延长保修服务所支付的金额要高于打印机的修理费。你应该时刻谨记为那些你无法轻松承受的意外上保险，而其他情况就不要浪费钱了，这是个人理财的核心原则之一。

有些事情可能会在不同时间段出现各种不同的意外状况，在面临这类复杂抉择时，预期值同样能够帮助我们理清思路。假设你的一个朋友建议你向一家研究中心投资100万美元用于开发男性防脱发产品，你或许会问成功的概率有多大，而你的朋友的回答很复杂。由于这是一个研发项目，因此研发团队研制成功的概率只有30%，如果最终研制产品失败了，那么你将收回25万美元，因为这部分资金原本是留着用于市场推广（用户测试、广告宣传等）的；即使最终产品研制成功了，美国食品药品监督管理局认为这一神奇的治疗脱发的产品对人体安全并批准进入市场的概率也只有60%；到了那个时候，即使我们的产品安全有效，依然还有10%的概率会出现一个强劲的竞争对手，带着更好的产品与我们一同进入市场，占据全部的市场份额。如果一切顺利—产品安全、有效，而且竞争者也没有出现，那么你将获得最多2 500万美元的投资回报。

你动心了吗？

朋友提供的信息量令人眼花缭乱。潜在的回报很诱人，回报的金额是投资额的整整25倍，在这一过程中，同样充满了各种潜在的陷阱和失败。如果每一个结果的出现概率都是准确的，那么画一张决策树形图，能够帮助我们理清信息，决定下一步应该做什么、怎么做。决策树形图标出了每一个不确定因素的来源，还有所有可能出现的结果及其概率。在树形图的下方，给出了所有回报可能的金额和概率。如果我们将每一个回报额乘以概率，再将得到的结果相加，就可以算出这一投资机会的期望值。通过观看下图能够帮助我们更好地理解问题。

图5–4　投资决策

如此看来，这项投资的预期回报是非常诱人的，高达422.5万美元。但我还是不建议你用辛辛苦苦积攒的、准备将来给孩子读大学的钱来进行投资。观察决策树形图，你会发现预期回报大大高于一开始的投资额，但不要忘记，最有可能发生的结果是研发失败，以致治疗男性脱发的产品最终没有面世，而你只能拿回剩下的25万美元。至于你对这项投资的胃口到底有多大，就要取决于你的风险倾向了。对此，大数定律给出的建议是，对于一家投资公司或像巴菲特这样富可敌国的个人投资者来说，应该尽可能地发掘上述例子这类结果不确定但预期回报很丰厚的投资机会，而且数量越多越好，几百个项目里面肯定有一些会成功，一些会失败，但平均来看，这些投资者最终会像保险公司或赌场那样挣到大钱。如果预期收益对你有利，那么涉足的项目越多，赚钱的机会就越大。

同样的道理，我们还可以用来解释一个有违直觉的现象。有时候，针对全美国人口监测如艾滋病这类罕见但严重的疾病是行不通的。假设我们对某种罕见病的检测拥有相当高的准确度，举例来说，每10万人中会有一个人患上某种疾病，检测准确率为99.999 9%，可以保证在检测过程中不产生一例伪阴性（也就是从不漏过任何一个患上该病的人），但产生伪阳性（也就是一个没有患上该病的健康人被误测为阳性）的概率为万分之一。这样就会导致一个棘手的状况，虽然这种疾病的检测准确率非常之高，但绝大部分被诊断为阳性（也就是患有该疾病）的人实际上根本没有得此病。这会在那些诊断结果为阳性的人群中产生巨大恐慌，后续的检测和治疗也会浪费有限的医疗资源。

如果我们对美国所有成年人，即约1.75亿人口进行检测，决策树形图如图5–5所示。

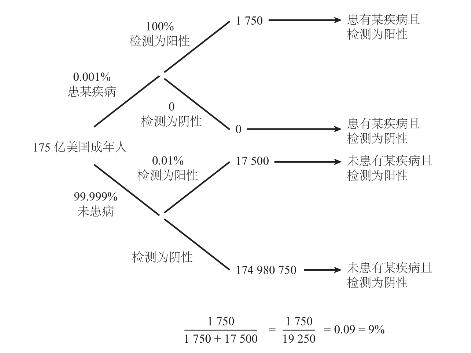
图5–5　某疾病全美国筛查情况

只有1 750位成年人患有该疾病，他们的检测结果均为阳性。有超过1.74亿成年人未患病，在这部分健康人群中，有99.999%的人得到了正确的检测结果，只有0.01%的人被误检为阳性。但1.74亿的0.01%依然是一个非常大的数字，因此在实际操作中平均将会有1.75万健康的人被告知患有该疾病。

这意味着什么？我们一起来分析一下。总共有19 250人的检测结果为阳性，但真正患病的只有9%，而且这还是一个准确性非常高、伪阳性非常低的检测。我想不需要作太多解释，大家就能理解为什么在削减医疗开支的过程中，我们该做的不是对健康人群加强疾病筛查，而是减少这类检测。以艾滋病为例，公共健康官员总是建议将有限的资源用在“刀刃”上，即用在男同性恋者、采取静脉注射的吸毒分子等高危人群身上。

有时候，我们能够借助概率发现一些可疑的事情。在第1章的内容里，我介绍了标准化考试过程中出现的组织作弊问题，还顺带提到了专门负责发现此类作弊行为的考试安全公司。而实际上，负责执行证券交易相关法律的美国证券交易委员会在稽查内幕交易行为的过程中，使用的也是类似的方法。（内幕交易包括非法使用内部信息来交易相关公司的股票或证券，如即将开展的公司收购—这类信息一般来说只有负责此事的律师事务所才知道）。美国证券交易委员会动用计算能力超强的电脑来分析数亿美元的股票交易，试图寻找可疑行为，如公司收购信息即将披露之前进行的大额股票购入、公司正准备宣布亏损前的大量抛售等。那些常年取得超高收益的投资经理们也是美国证券交易委员会的重点调查对象，因为无论是经济理论还是历史数据都告诉我们，每年的收益都超过平均水平对于一个投资者来说，几乎是不可能的。当然，聪明绝顶的投资者们总是能够预测到市场的走势，在法律允许的范围内设计出完美的投资策略，获得高于市场平均数的收益。一个好的投资者不一定非得使用不正当的手段，不过电脑是怎么区分好人和坏人的呢？我多次致电美国证券交易委员会的执法部门，咨询他们是借助哪些模型来确定犯罪行为的，但他们至今也没有给我回复。

在电影《少数派报告》（2002）中，汤姆·克鲁斯扮演的是一位预防犯罪探员，借助科技手段在坏人作案之前，预测他们的犯罪行为。

2002年，这部电影还只是一部科幻片，但到了2011年，这就成了现实。《纽约时报》在这一年刊登了一篇报道，标题为“在犯罪发生前派遣警力”，讲的是圣克鲁兹市警察局的电脑程序预测出闹市区的一个停车场将有可能发生汽车盗窃案件，于是自动派遣了一队警察前往现场，到场的警察随后逮捕了两个形迹可疑、偷瞟车窗的女人，其中一个人是警局的常客，另外一个人身上携带着毒品。

圣克鲁兹市的电脑程序是由两位数学家、一位人类学家和一位刑事学家共同设计的。芝加哥警察局还专门设立了一个犯罪预测分析小组，原因是这个城市的暴力犯罪主要源自团伙作案，而这些团伙的作案手段往往有规律可循。在《数据挖掘和预测分析：情报收集和犯罪分析》一书中，作者将统计学运用到执法过程中，开篇是这样写的：“目前在犯罪侦查领域，预测未来已经成为可能，诸如识别犯罪趋势、判断社区热点、优化资源调度等，以求最有效率地为市民提供最多的保护。”（对了，这些内容我总结给你们看就行了，亲爱的读者们就不必费心再去读那本书了。）

“预测执法”属于预测分析学的一部分。犯罪总是带有不确定的成分，就好像没有一方能够确切地说谁会撞车、谁会还不起贷款。在面临这些风险时，概率学能够帮助我们走上正确的分析道路。此外，信息的收集和积累能够让我们更好地理解相关事件的概率。在充满不确定性的商业世界里，商人们总是希望能够将他们的风险量化，放贷者会要求查看贷款人的收入证明和信用评分，但这些迟钝的信用工具在预测未来方面的作用充其量不过是史前洞穴人手中的石器，大量的电子数据和廉价的电脑计算才真正能够为我们揭示人类的行为。保险推销员准确地将他们的行业描述为“风险转移”，因此他们最好先理解转移的风险究竟是什么。像好事达这样的保险公司之所以成功，是因为它们知道并重视那些在别人眼里可能毫无关联的随机事件：

● 年龄为20～24岁的司机最有可能造成致命交通事故。

● 在伊利诺伊州最经常失窃的车是本田思域（亚拉巴马州为全尺寸雪佛兰皮卡）。

● 一边开车一边发短信容易造成事故，但各州出台的禁止开车发短信的法律似乎并没有遏制这种行为。事实上，这些法律甚至有可能让情况变得更糟，因为司机在发短信时会想办法将手机藏得更为隐蔽，更加不把心思放在专心开车上。

信用卡公司一直处于这类分析法的前沿，原因有二：这些公司的数据库里保存着大量有关我们消费习惯的数据，而且它们的商业模式离不开那些信用风险适中的客户。那些拥有最佳信用记录的客户每个月总能准时付清账单，信用卡公司没法从他们身上赚得一点儿利息；那些账单数额巨大且经常忘记按时还款的客户才是信用卡公司的“金主”，高额的利息给公司带来了丰厚的利润，只要这些客户不违约就行。经营汽车产品及其他零售商品的加拿大轮胎公司有一位“爱好数学的首席执行官” J·P·马丁，他专门研究在面对商品时，哪些人更愿意掏钱消费，而哪些人倾向于转身离开。这是一个非常有趣的课题，马丁对上一年使用加拿大轮胎联名信用卡消费的每一笔交易数据进行了数据分析，发现在综合考虑收入、信用纪录等传统统计指标的基础上，观察消费者购买了什么商品能够准确地预测出他们接下来的消费行为。

《纽约时报》上一篇标题为“你的信用卡公司对你知道多少？”的文章描述了马丁发现的一些有趣现象：“选择购买价格便宜、通用汽油的消费者有错过信用卡还款日期的可能，而那些选择高档名牌商品的消费者倒是经常按时还款，那些会为家里添置一氧化碳探测器或凳脚套防止刮伤地板的人几乎从来不会延期还款，所有购买骷髅头造型汽车挂饰或对汽车的排气系统进行大排量改装的人基本上不会按时还款。”

当我们在生活中遇到不确定因素时，概率学是一个可靠的参考工具。你不应该购买彩票；如果你有一个长远的投资视野，那么你应该把钱投入股市（因为股票是能够带来长期收益的一种典型投资品种）；你应该为某些东西购买保险，其他东西就算了；概率学甚至还能助你在游戏竞赛节目中扩大赢面（下一章内容就会讲到）。

虽然说了（写了）这么多，但还是要再多说一句：概率并不是确定的。你不应该购买彩票，但你依然有可能通过购买彩票发财。是的，概率学能够帮助我们揪出作弊者、追踪大坏蛋，但若使用不当，我们就有可能把无辜的人送进监狱。这就是为什么我要写第7章的内容。