相关性与相关系数的定义和计算方法

Naked Statistics

视频网站根本不知道我是谁，但它又是怎么知道我喜欢看人物纪录片而不是电视连续剧、动作片或科幻片的？

有一段时间，每当我打开网飞视频的页面，总是会弹出一条收看提示，建议我观看纪录片《布托》—一部关于巴基斯坦前总理贝娜齐尔·布托的生平与悲惨遭遇的“富有深度与煽动性”的电影。我对这部电影的印象不错，而且也把《布托》加入到了我的观看列表中。最神奇的是，在那些网飞推荐给我的影片中，如果是我之前看过的影片，那么毫无疑问这些影片都是我非常喜爱的。

网飞公司是如何做到这一点的？在其公司总部是不是有一大群实习生，整天在谷歌网站上搜索有关我的信息，并综合了我的家人和朋友的观影兴趣，得出我可能会对一位巴基斯坦前总理的纪录片感兴趣的结论？当然不可能。网飞公司只不过是掌握了一些非常复杂、精密的统计学手段。网飞公司甚至根本不知道我是谁，但却知道我过去喜欢看什么类型的电影（因为我曾经在网站上为这些电影打过分）。基于这一信息，再加上其他用户的评分以及一台强大的电脑，网飞公司对于我的电影品位的预测精准得令人震惊。

我将会告诉大家网飞公司做出这些预测的具体算法，现在最重要的一点是：这所有的一切都基于相关性。网飞向我推荐的电影与我喜欢的其他影片类似，此外，该网站还向我推荐得到某些网友高度评价的影片，而这些网友的打分恰恰与我的打分非常接近，可以说这些网友是一群与我“臭味相投”的观影者。纪录片《布托》之所以会出现在我的网页上，是因为我给另外两部纪录片打了满分五颗星，这两部影片分别是《屋内聪明人》和《战争之雾》。

相关性体现的是两个现象之间相互关联的程度，例如在夏天，温度的高低与冰淇淋的销量就存在相关性，当温度升高时，冰淇淋的销量也会相应提高。如果其中一个变量的改变引发另一个变量朝着相同的方向变化，那么我们说这两个变量存在正相关性，就比如身高与体重之间的关系，（一般来说）个子高的人体重会重些，个子矮的人体重会轻些。如果一个变量的改变引发另一个变量朝着相反的方向变化，那么这两个变量就存在负相关性，比如锻炼与体重。

凡事都没有那么简单，有些时候也会出现与上述相关性相违背的现象。有些个子矮的人就是比个子高的人重一些，有些从来不运动的人甚至比运动爱好者苗条，但无论怎样，身高与体重、锻炼与体重之间总是存在着有意义的关联。

如果对美国成年人的身高、体重进行随机取样，我们会得到如下一幅散点分布图：

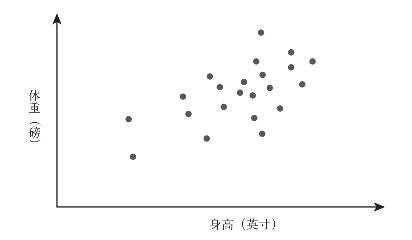
图4–1　身高与体重散点分布图

如果我们要绘制一幅关于锻炼（每周进行剧烈运动的分钟数）和体重的散点分布图，就会看到一个相反的趋势，即运动量越大体重越轻。但是，这样一张完全由分散的点构成的图怎么看都不像是一个简便易行的统计工具。设想一下，如果网飞公司是以这种方式向我推荐影片的，那么公司总部估计早已被数百万名用户的评分散点淹没了。与之相反，相关性作为一个统计工具的魅力就在于将两个变量的关联精炼成一个描述性数据：相关系数。

相关系数拥有两个无与伦比的优势。第一个优势体现在数学表达上，从本章后面的内容中我们能够发现，相关系数是一个区间为–1到1的常数。如果相关系数为1，即完全相关，表示一个变量的任何改变都会导致另一个变量朝着相同方向发生等量的改变。如果相关系数为–1，即完全负相关，代表一个变量的任何变化都将会引发另一个变量朝着相反方向发生等量的改变。

相关系数越接近1或–1，变量间的关联性就越强。如果相关系数为零（或者接近零），则意味着变量之间不存在有意义的联系，就比如一个人的鞋码和高考成绩之间的关系。

第二个吸引人的优势在于，相关系数不受变量单位的限制。我们可以计算身高和体重之间的关联性，哪怕身高和体重的单位分别是英寸和磅。我们甚至还可以计算出高中生家里的电视机数量和他们的考试成绩之间的关联性，而且我敢保证是正相关（之后的内容中我会给出解释）。这就是相关系数能够为我们完成的一件非常神奇的事情：将大量芜杂无序、单位不统一的复杂数据（就比如上面的身高、体重散点分布）加工成一个简洁、优雅的描述性数据。

实现过程是怎样的？

跟之前一样，我已经在本章后面的内容添加了一个常用的相关系数计算公式。相关系数通常不是一个徒手计算出来的统计参数，而是需要借助微软Excel办公软件或其他办公软件，你只需要输入数据，软件就会自动求得两个变量之间的相关系数。整个过程理解起来并不是很难，相关系数的计算过程如下：

1.计算出两个变量的平均数和标准差。还是以身高和体重为例，我们会得出样本人群的平均身高和平均体重，以及它们的标准差。

2.对所有数据进行转换，表现为距离（也就是标准差）的形式。请紧跟我的讲述，这一步并没有你想的那么复杂。假设样本的平均身高为66英寸（标准差为5英寸），平均体重为177磅（标准差为10磅）。如果你的身高为72英寸，体重为168磅，就表明你高于平均身高1.2个标准差，用公式来表述即为[（72–66）/5] =1.2，轻于平均体重0.9个标准差，即[（168–177）/ 10]=–0.9。的确，如果你的身高高于平均身高，体重却轻于平均体重，我们可以用“异常”来形容，但是既然你花钱买了我的书，那我就不能不手下留情—暂且说你又高又苗条吧。注意了，在此之前你的身高和体重数据后面还紧跟着单位—“英寸”和“磅”，现在却被转换成了简简单单的1.2和–0.9，单位神奇地消失了。

3.到了这一步，我只需要，让电脑来完成剩下的工作。通过公式，电脑会整合样本里所有人的身高和体重的标准差数据，并最终为我们揭示身高和体重之间的关系。假如样本中有些人的身高高于平均值1.5或2个标准差，那么他们的体重相对于平均值来说会呈现一种什么状况？那些身高接近平均值的人，他们的体重又会有什么变化？

如果一个变量和平均值之间的距离与另一个变量和平均值之间的距离在相同方向上高度吻合（例如，身高特别高或矮的人的体重一般也会特别重或轻），那么我们就可以断言这两个变量之间存在着强烈的正相关关系。

如果一个变量和平均值之间的距离与另一个变量和平均值之间的距离在相反方向上高度吻合（例如，锻炼时长大大高于平均值的人，他们的体重也大大低于平均值），那么我们就可以断言这两个变量之间存在着强烈的负相关关系。

如果两个变量无论在什么分析模式下都无法呈现出规律（例如鞋的尺码和锻炼时长），那么这两个变量之间就不存在或基本不存在相关性。

上述的内容让大家受苦了，好消息是我们马上就要谈到轻松的付费电影话题了。但在此之前，我们先来聊聊生活中另一个与相关性息息相关的事物：SAT考试。是的，就是大名鼎鼎的美国学术能力测试，也叫SAT推理测验。这一标准化考试由3部分组成：数学、阅读和写作。或许你曾经参加过SAT考试，或者很快你将参加这项考试，但是你很有可能从来没有想过参加这个考试到底有什么意义。该测试的目的在于，检验学生的学术能力，并预测他们进入大学后的表现。当然，有人会问（尤其是那些不喜欢标准化考试的人）：这难道不是高中应该做的事吗？难道在大学招生老师的眼里，一场历时4个小时的考试难道比高中4年的成绩都重要？

这些问题的答案其实都隐藏在第1章和第2章的内容里。高中时期的成绩是一个有缺陷的描述性数据。一个选修了数学、科学等挑战性较大的课程的学生，可能期末成绩很一般，但其学术能力和潜力可能要优于那些虽然成绩很好但选的课程都较为简单的同校同学。如果将多个学校进行横向比较，那么这类差异就会更大了。美国大学委员会负责SAT测试的出题和管理，据委员会成员介绍，SAT测试的初衷就在于“让每位学生在申请大学时都能得到公平的对待”。说得对！SAT将学生能力进行了标准化加工，让大学在录取学生时有了一个简单明了的参考标准。但SAT测试究竟是不是一个好的能力评价标准呢？想要找一个评价学生的统一标准并不难，我们可以让所有的高中毕业生来一个百米测试，也能分出优劣，而且比SAT花费少和易于操作。不过有一个问题，百米短跑的成绩与大学表现可以说毫不相关，这是两个不相关的变量，虽说数据收集并不费劲，但它也不会告诉我们有意义的情况。

那么，SAT在这方面的表现如何？我有一个不幸的消息要告诉未来的高中毕业生，SAT成绩在预测大学一年级学生的成绩方面表现得相当不错。美国大学委员会定期会发布相关性报告。零代表毫不相关，1代表完全相关，学生的高中平均成绩与大学第一年的平均成绩之间的相关系数为0.56（为了让大家有一个直观的比较，我为大家提供一个数据，那就是美国成年男子身高和体重之间的相关系数大约为0.4），而SAT综合成绩（阅读、数学和写作）与大学第一年的平均成绩之间的相关系数同样为0.56。既然SAT测试在预测学生大学表现方面并没有比高中的平均成绩更优秀，那为什么还要设立这样一个考试呢？事实上，如果将SAT成绩和高中平均成绩综合起来，就能得到一个相关系数为0.64的最佳预测指数。所以，亲爱的同学，我只能说抱歉了，乖乖地准备SAT考试吧。(www.xing528.com)

在本章的讨论过程中，我们必须牢记一点，那就是相关关系并不等于因果关系。两个变量存在正相关或负相关的关系，这并不代表其中一个变量的改变是由另一个变量的变化引起的。举个例子，之前我提了一句，学生的SAT成绩和其家里的电视机数量呈正相关关系，但这句话的意思并不是说望子成龙的家长多买5台电视机摆在家里，孩子的成绩就能提高了，也不是说，学生在家多看电视有助于提高学业成绩。

对这样一个相关性最符合逻辑的解释应该是，受过良好教育的家长既能买得起多台电视机，也能很好地辅导孩子的学习，使其在考试中发挥出色。电视机的数量和考试分数很可能都是由第三个变量—家长的受教育程度决定的。我无法证明家中拥有电视机的数量和孩子的SAT分数之间的相关性（因为教育委员会并没有提供这方面的数据），但我能证明家境殷实的孩子的SAT分数要普遍高于家庭生活条件相对困难的学生。美国教育委员会提供的数据显示，家庭年收入超过20万美元的学生，他们的SAT数学平均分为586；而家庭年收入低于两万美元的学生，他们的SAT数学平均分仅为460。与此同时，年收入高于20万美元的家庭也极有可能（在多个房产内）拥有多台电视机，电视机数量势必要多于年收入低于两万美元的家庭。

几天前，我开始了本章内容的创作，也借此机会观看了纪录片电影《布托》。太精彩了！这是一部关于一个伟大家庭的伟大电影。详细的影像资料，从1947年印度和巴基斯坦分治一直到2007年贝·布托遇刺，让人看来荡气回肠。布托的演讲和采访原音穿插全片，贯穿她的一生。观毕此片，我毫不吝啬地打了5颗星，完全符合网飞的预测。

归根结底，网飞运用的还是相关性的概念。我在网站上给以前看过的电影评分，网飞将我的评分与其他用户进行比较，从中筛选出与我相关性最高的用户，这些人的电影品位可以说与我是最接近的。数据库一旦建立，网飞就会向我推荐那些与我品位相同的用户打了高分，而我又恰好没有看过的电影。

当然，这只是简略的介绍，真正的方法要比这个复杂得多。2006年，网飞公司发起了一场比赛，邀请公众参与设计影片推荐机制，以帮助网飞在现有的推荐方案上提高至少10%的准确率（即用户在观看完推荐影片后给出的评分正好对应网站之前的预测），比赛赢家可以获得100万美元的奖励。

报名参赛的个人或团队都会收到一套“训练数据”，包含了48万名网飞注册用户对1.8万部电影共计1亿多次的评分，但其中有280万个评分是“保密”的，即只有网飞公司知道评分的具体结果，参赛者是不知道的。参赛者需要通过自己的算法和程序，来预测出这些“保密”评分的内容，网飞公司会根据每位参赛者所提交的内容来判断其准确程度。在超过3年的时间里，有来自180多个国家的团队提交了改进方案，但在参评之前他们必须满足两个条件：第一，获胜者必须将算法程序授权给网飞公司；第二，获胜者必须“向全世界描述你是如何做到的”。

2009年网飞公司终于宣布了比赛的最终结果：获胜者为一个7人团队，由统计学家和计算机专家组成，他们分别来自美国、奥地利、加拿大和以色列。遗憾的是，我无法在这里向各位介绍他们的获胜系统，就算本章的补充知识点对此也没有提及，因为他们的成果介绍长达92页纸。网飞影片推荐系统的品质毋庸置疑，但无论包装如何精美，说到底还是一件十分普通的事，甚至早在电影工业初期就已经出现了：找几个跟你有相同趣味的人并让他们向你推荐一些电影。既然你那么爱看我喜欢的电影，厌恶我认为不好看的电影，那么你觉得乔治·克鲁尼的新片怎么样？

这就是相关性的真谛。

本章补充知识点

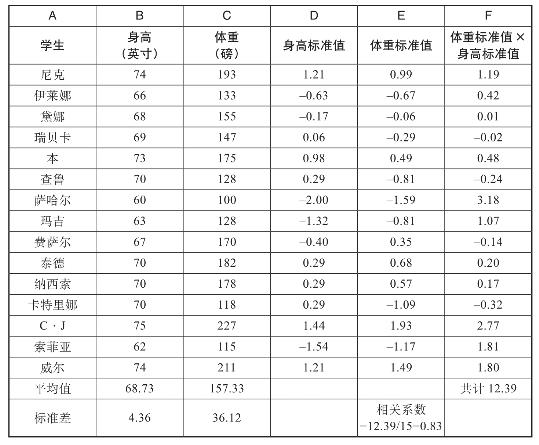
要计算两组数据的相关系数，我们需要按以下几个步骤进行。为了让大家能够更好地理解，这里每个步骤的讲解都是基于一张15个学生的身高与体重的数据表。

1.将每个学生的身高转换为标准值：（身高–平均身高）/ 标准差。

2.将每个学生的体重转换为标准值：（体重–平均身高）/ 标准差。

3.将每个学生的体重标准值和身高标准值相乘，你会发现，当一个学生的身高和体重都偏离平均值较远时，乘积的绝对值也会较大。

4.将第三步求得的乘积相加，再除以统计对象的数量（在这个例子中为15），就可以得到相关系数。

这一组学生的身高与体重的相关系数为0.83，考虑到相关系数的范围是从–1到1，因此我们可以认为身高和体重之间存在着较强的正相关关系。

在我们介绍相关系数的公式之前，有必要了解几个数学符号。求和符号Σ是一个常用的统计学运算工具，表示跟在其后的数据的总和。假设有一组数据x1、x2、x3和x4，那么Σ（xi）就意味着我们应该将4个数相加：x1＋x2+x3+x4，即Σ（xi） = x1+x2+x3+x4。那么，这组数据的平均值公式就为：平均值 =Σ（xi）/n。

如果用更符合数学规范的格式来表述，那么求和公式就应该写成：

表示x1+x2+x3+……xn，求和公式的第一项为x1（当i = 1时），最后一项为xn（当i = n时）。对于n个数据来说，其平均值公式就可以表示为：

再加上其他通用符号，变量x和y的相关系数r的运算公式可以表示为：

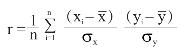
其中，n代表数据个数，x¯ 代表变量x的平均值，y¯ 代表变量y的平均值，σx代表变量x的标准差，σy 代表变量y的标准差。

所有统计软件都具备计算两个变量的相关系数的功能。例如，用微软Excel办公软件来解决之前15个学生的身高和体重的相关性问题，电脑运算得到的相关系数与手动计算的结果是一致的，都是0.83。