统计数字的迷思：揭秘数字会撒谎的真相

Naked Statistics

1950年人们的平均时薪是1美元，2012年人们的平均时薪是5美元，你觉得我们的工资水平涨了吗？

对于任何一个约会过的人来说，通常会对“他这人还不错”这类表述引起警惕，不是因为这句描述一定是错误的，而是因为这句话中还有其他潜台词，诸如其实这个人曾经坐过牢，或者他的离婚手续“还没完全办妥”等。我们丝毫不怀疑他的人品不错，只不过担心这么一句看似正确的陈述，其用意可能在于掩饰或淡化其他信息，从而误导听者（我想不会有人愿意与一个还没离婚或有重罪案底的人约会吧）。这类陈述严格来讲并不能被称作谎言，哪怕你跟人说了也不会被判伪证罪，但由于其准确性实在不敢恭维，所以最好不要相信。

统计学也是如此。虽然统计学是扎根于数学土壤里的，而且数学又是一门以准确著称的学科，但使用统计学来描述复杂现象的这一过程并不是精确无误的，这就为掩盖真相创造了大量的空间。马克·吐温有一句名言是这样说的,“谎言有三种：谎言、该死的谎言，以及统计学”。正如前一章所讲的，我们关心的大多数现象都可以用多种方式进行描述。如果对某一事物的描述存在多种方式（如“他人不错”或“他曾经因证券欺诈罪被判入狱”），那么我们所选择使用（或回避）的描述性数据就会影响别人对此事的印象。一些别有用心的人甚至会用光鲜的事实和数据来支持真假存疑或完全不成立的结论。

首先，我们应该弄明白“精确”和“准确”这两个词之间至关重要的区别。这两个词不可以相互替代。“精确”反映的是我们描述事物的精度，比如在描述你从家到公司的距离时，“41.6英里”就比“大约40英里”更精确，当然比“相当长的一段路”更精确一些。如果你问我最近的加油站在哪里，我会告诉你往东1.265英里，这就是一个精确的回答。但问题也随之而来：如果加油站在西边，那么这样的一个回答就是完全不准确的。也就是说，如果我告诉你：驾车大约10分钟，当你看到一家热狗售卖摊点时，加油站就在你的车右前方几百码的地方，如果你经过猫头鹰餐厅，就说明你的车开过了。这样的一个回答虽然没有“往东1.265英里”那么精确，但显然更好，因为我为你指明了前往加油站的正确方向。一个数据的准确与否表明了其与真相是否一致，因此将“精确”和“准确”混为一谈是要付出代价的。如果一个答案是准确的，那么在这个基础上当然是越精确越好；但如果答案从一开始就是不准确的，那么再精确也毫无意义。

让我意识到“精确”和“准确”的区别的，是一件发生在某个圣诞节的事情。那一天，我的妻子给我买了一个高尔夫测距仪，以便让我测量高尔夫球到球洞之间的距离。这个设备是通过某些激光原理进行工作的，我站在高尔夫球旁，然后将测距仪对准远处草地上的球洞杆，之后仪器上就会显示我应该击球的精确距离。相比起原始的标准码数标记来说，这个设备在性能方面有了很大的提升，因为原先我们只能通过看场上的标记来估算出测量位置与球场中心的距离（因此，测距仪让高尔夫球这项运动变得更加精确，但却更加不准确）。通过这个高尔夫测距仪，我终于知道了我的球离球洞还有147.2码。我期待这一先进的技术能够助我提升球技，但事实是，我打得越来越差。

这里有两个问题。第一，在我用了这个设备3个月的时间之后，我才猛然意识到计量单位是“米”而非“码”，因此，每一次看似准确的测量（147.2）都是错误的。第二，有些时候我会不小心地将激光束对准球场后面的树干，而非球洞杆，因此我的“完美”击球就会导致“完美”的结果—在空中划出一道漂亮的弧线，然后越过整个球场落入森林里。这个例子告诉我，即使是最为精确的计算或测量都应该检查一下是否符合常识。这一点适用于所有的统计分析。

再举一个严肃一点儿的例子。在2008年金融危机爆发之前，华尔街的许多风险管理模型都非常精确，“风险值”的概念让这些公司得以将其在不同情况下可能损失的资产进行精确量化，但问题是，这些超级复杂的模型就好比是将我的高尔夫测距仪的长度单位设置成“米”而不是“码”。数学运算极为复杂和晦涩，得出的结果精确到几乎没有人会怀疑其真实性。但嵌入这些模型中的有关全球市场可能会发生的风险假设其实是错误的，因而精确计算所得出的结论从根本上说就是不准确的，这不仅坑苦了华尔街，更是把全球经济都“拖下水”。

即使是最为精确和精密的描述性数据，都有可能面临一个根本性的问题：缺乏清晰度，不知道我们到底要定义、描述或解释什么。统计参数与失败的婚姻有着许多共同点，争论双方往往都说服不了对方。思考一个重要的经济问题：美国的制造业有多健康？人们经常能够听到，美国的制造业正在失去大量的工作机会，这些工作岗位源源不断地流向中国、印度以及其他低工资国家。人们还能够听到，美国的高科技制造业依然坚挺，美国依然是世界上最大的商品出口国之一。到底哪个说法才是对的？这就涉及统计学的另一个方面：对优质数据的合理分析能够有效地调和对立的观点。美国的制造业是有利可图且在国际上有竞争力，还是面临激烈的外国竞争正处于萎缩的过程之中？

答案是两者兼有。英国新闻杂志《经济学人》通过下面的曲线图将看上去似乎矛盾的两个观点融合在了一起，为我们展现出一幅关于美国制造业的趋势图。

图3–1　“铁锈地带”的复苏

这一对看似矛盾的观点取决于我们如何定义美国制造业的“健康状况”。从生产和所售商品的总价值—产出来看，美国的制造业自2000年以来一直保持稳定增长，直到2008年的经济大衰退才遭受重创，而此后又出现了强劲反弹。这一点与美国中情局的《世界概况》里的数据相吻合，美国是世界上第三大制造业出口国，排在中国和德国之后。如今，美国依然是一个制造业大国。

但《经济学人》杂志刊登的曲线图上还有一条曲线，展示了美国制造业的就业状况。美国制造部门的岗位数量一直处于下降之中，在过去10年时间里有差不多600万人丢了饭碗。这两个故事—增加的产出和减少的工作岗位—共同组成了关于美国制造业的一个完整的故事。美国制造业的生产力在不断提升，也就是说，工厂可以通过雇用更少的工人来完成更多的产出。这一点从国际竞争的角度来说是有利的，因为美国制造的商品相比低工资国家来说更具市场竞争力（与一家仅能支付时薪两美元的公司抗衡的方式之一，就是提高生产效率，让自己的公司在支付时薪40美元的同时，将工人的生产效率提高到对手公司的20倍）。如果这样的话，制造行业所需的岗位就会大大减少，这对于那些亟须这点儿工资养家糊口的失业工人来说是一个巨大的打击。

既然本书讲的是关于统计学而非制造业的知识，那么就让我们言归正传，来谈谈美国制造业的“健康状况”。如何评价一个行业是否健康，这一点量化起来似乎并不难，就看我们如何选择了，是选择以产出量还是就业率为衡量标准？在这个例子（以及许许多多其他的例子）中，最完整的故事往往都会包含两方面，《经济学人》在上图中就作了明智的示范。

即使我们对成功的衡量标准达成了某个共识，比如说学生的考试分数，仅此一项统计还是会有充裕的欺骗空间。举个例子，下面的两个陈述句都可以说是正确的，但看看你是否能够将这两者调和在一起。

政客甲（挑战者）：“我们的教育水平正变得越来越糟！2013年有6成学校的考试成绩低于2012年。”

政客乙（在任者）：“我们的教育水平正变得越来越好！2013年有8成学生的考试成绩高于2012年。”

给大家一点提示：并不是所有学校的学生人数都是一样的。如果我们回过头来再看这两句似乎相互矛盾的陈述，你会发现政客甲将学校当作其分析单位（“有6成学校……”），而政客乙则是将学生作为其分析单位（“有8成学生……”）。在统计学中，分析单位是作为比较或描述的对象而存在的—其中一位政客选择了学校的表现，而另一位政客选择了学生的表现。如果成绩上升的学生正好来自办学规模非常大的学校，那么大部分学生在学业上有所进步而大部分学校的成绩正在退步，这两者是完全有可能同时发生的。为了让这个例子更加直观，我们可以用美国各州的经济情况进行说明。

政客甲（平民主义者）：“我们的经济一塌糊涂！2012年有30个州的收入都出现了下滑。”

政客乙（更接近精英派）：“我们的经济走势一片光明。2012年有70%的美国人的收入都增加了。”

从这两句话中，我能读出的信息是：诸如纽约、加利福尼亚、得克萨斯、伊利诺伊等州的经济形势最好，而收入下滑的那30个州更有可能是规模比较小的州，如佛蒙特、北达科他、罗德岛等。由于各个州的面积大小不同，大部分州的经济下滑和大部分美国人的收入上升是完全有可能同时存在的。关键就在于分清分析单位，描述的对象到底是谁（或什么），以及不同的人口中的谁（或什么）是不是存在差异？

刚刚举了两个虚构的例子，而接下来的这个例子是一个真实且至关重要的统计学问题：世界各地人民的收入不均衡因为全球化的到来是改善了，还是恶化了？一种理解是，全球化只是加剧了现有的收入不均状况，1980年时的富裕国家（以人均国内生产总值为参考）在之后的20年间的增长速度超过了贫困国家。富国会变得更富，这说明贸易、外包、外国投资以及其他全球化的组成部分沦为了发达国家扩大经济霸权的工具。

如果换一种分析单位，同样的数据也可以（也应该）以一种完全不同的方式来解读。我们不关心穷国，我们只关心穷人。恰巧世界上有绝对比例的穷人生活在中国和印度，这两个国家都是人口大国（人口数量均超过10亿），而且在1980年的时候这两个国家都处于相对贫穷的发展阶段。但是，在过去的几十年时间里，中国和印度的经济都经历了高速发展，这在很大程度上要归功于它们与世界上其他国家日益加深的经济一体化。《经济学人》这样评价中国和印度：“它们都是‘迅速的全球化者’。”考虑到我们的目的是改善人类本身的穷困，因而在衡量全球化给全世界穷人带来的影响时，将中国（13亿人口）和毛里求斯（130万人口）当成是比重相同的两个国家来看待是不合理的。

上述例子的分析对象应该是人，而不是国家。1980～2000年这20年的时间到底发生了什么？回想一下刚刚那个虚构的学校例子。世界上的大部分穷人恰好都生活在两个大国里，而这两个大国在融入全球化的过程中都经历了经济的飞速发展。正确的分析得出了一个截然不同的结论：全球化有利于全世界的穷人。《经济学人》杂志指出：“如果你考虑的是人而不是国家，那么全球不平等现象正在迅速减少。”

美国的两家电信业巨头美国电话电报公司和威瑞森电信最近卷入了一场广告之争，说白了也是因为模棱两可的描述所引发的。这两家公司都提供移动通信服务，对于绝大多数的手机用户来说，他们最关心的问题无非就是服务网络的覆盖范围和通话质量，最不愿看见的就是在需要拨打或者接听电话时却没有信号。因此，从逻辑上讲，要比较这两家公司孰好孰坏，只要看它们各自通信网络的规模和质量就行了。为了迎合消费者对于更大、更好的网络覆盖的需求，两家公司在衡量这一看不见、摸不着的需求时采取了不同的分析指标。威瑞森电信公司发动了一场声势浩大的广告战略，四处兜售其无所不在的网络覆盖，给消费者留下这样一个印象：在辽阔的美国国土上，威瑞森电信公司的基站几乎遍布全美国的各个角落，而与之形成对比的，是美国电话电报公司的相对零碎的地理覆盖。威瑞森电信公司所选择的分析单位是网络覆盖的地理范围，这是因为这家公司的确在这方面要强一些。

与此同时，美国电话电报公司也发动了反击战，选择了另一个分析单位。在其巨大的广告牌上赫然写着“美国电话电报公司能够满足97%的美国人的通信需求”，注意这里的用词是“美国人”，而不是“美国”。美国电话电报公司所强调的重点在于，绝大多数的美国人并不住在蒙大拿州的偏远乡村或是亚利桑那州的沙漠之中，既然美国的人口在地理上来说并不是平均分布的。这则广告的言下之意就是，一个好的通信服务网络的关键就在于，将服务重点放在那些手机用户真正生活和工作的区域，而不是他们偶尔才会去野炊的地方。但由于我经常要回新罕布什尔的乡下，因此在这个问题上，我可能还是会选择威瑞森电信公司作为我的移动电话服务商。

我们的“老朋友”平均数和中位数同样会被心术不正的人利用。在上一章的内容中我们介绍了这两个概念，希望大家还能回忆起来，无论是平均数还是中位数，都是衡量一组数据的“中间位置”或“中心趋势”。平均数就是所有数据求和之后再除以个数（3、4、5、6、102的平均数是24）。中位数就是一组数据最中间的那个点，有一半数据位于这个点之前，有一半数据位于这个点之后（3、4、5、6、102的中位数是5）。现在，聪明的读者一定会注意到24和5之间存在着巨大的差异。所以，如果出于某种考虑，想要让这组数据在描述时显得数值大一些，那么我会选择求它们的平均数；但如果我想让数值看上去小一些，我肯定会将关注点放在中位数上。

现在，我们来看一下这在现实生活中是怎么操作的。以美国前总统小布什的减税政策为例，根据小布什政府的说法，这一政策将惠及绝大多数的美国家庭。相关政府官员指出，在这项政策推行之后，将会有9 200万美国人享受减税待遇，人均减税额超过1 000美元（具体数字应该是1 083美元）。但这个关于减税政策的概括准确吗？《纽约时报》评价说：“数据本身并没有撒谎，只不过有些数据没有发出声音罢了。”

是不是会有9 200万美国人将享受减税待遇？答案是肯定的。

那么，这些人中的大部分人都可以少缴纳约1 000美元的税款吗？不是的。因为减税额的中位数还不足100美元。

只有数量相对少的巨富们才有资格享受大额减税，而正是这些人拉高了平均值，让人均减税额看起来比绝大多数美国人真正享受到的要高。中位数对异常值并不敏感，因此在这个例子中，如果要看小布什政府的减税政策对普通家庭的影响，中位数可能会是一个更为准确的描述性数据。

当然，也正是因为中位数对异常值不敏感，所以在某些情况下中位数同样会掩盖事实真相。假设你患上了某种不治之症，好消息是有一种新药刚刚研发出来，可能会对你的病产生积极疗效，坏消息是这种药的价格非常昂贵，而且副作用有很多。“真的有效吗？”你会对这种药充满疑惑。医生告诉你这种新药能够延长患此疾病的病人的“半数预期寿命”（也就是这些病人寿命的中位数）达两周。这根本就算不上是什么好消息，相比起那么贵的药价和不良反应，这两周的寿命不要也罢。同时，你的保险公司也拒绝为这项治疗承担费用。这是一个基于半数预期寿命的典型案例。

但在这个例子中，中位数或许会成为一个相当有误导性的数据。假设有许多病人对这种新药完全没反应，但同时也有相当数量（30%～40%）的病人完全治愈了。然而，后者的成功并不能在中位数中得到体现（虽然接受新药治疗的病人的平均寿命看上去非常令人振奋）。对你而言，与你自己高度相关、真正影响你决定的反而是那些接受了新药治疗并活了很多年的病人，也就是统计学里的异常值。而且，这并不是一个虚构的例子。进化生物学家史蒂芬·杰·古尔德曾经被诊断出患有某种癌症，他的半数预期寿命只有区区8个月。但20年过去了，古尔德死于另一种不相关的癌症。古尔德生前写过一篇非常有名的文章，题目为“中位数不等于真信息”，他在文章里指出了他只能活8个月是一个错误结论，并表示是他头脑里积累的统计学科学知识将他从错误的结论中拯救了出来。中位数的定义告诉我们有1/2的病人活不到8个月，但另外1/2的病人至少可以活8个月，或者比8个月的时间更长（甚至是活到老），其死亡分布是“右偏”的。因此，如果你恰好患上了这种病，这一数据的意义要比一个单纯的技术术语丰富得多。

上述例子表明，中位数的决定性特征—不考虑数据距离中间位置有多远或是多近，而是关注它们是高于中间位置还是低于中间位置—反而成为它的弱点。与之相反，平均数恰恰是由数据分布决定的。从准确性的角度来看，平均数和中位数孰取孰舍，关键就在于这个数据分布里的异常值对事实的真相是起到扭曲的作用，还是其重要的组成部分。再次强调，判断比数学更重要。当然，没有人强制你一定得选中位数或平均数，任何一个复杂综合的数据分析都会包含这两个数据。所以，当只有其中一个数据出现的时候，你就要注意了，有可能只是出于言简意赅的考虑，但也有可能是某些人别有用心地想用数据“说服”你。

上了一定年纪的人或许会记得一部《疯狂高尔夫》的电影，里面的两位主演分别是塞维·蔡斯和泰德·奈特，他们在高尔夫球场的更衣室里有过这么一段对话：

泰德：刚刚打得怎样？

塞维：啊，我没记数。

泰德：那你用什么跟别人比啊？

塞维：身高。

我引用这段电影台词的目的不是想说明它有多幽默，而是想说其实统计学里也有很多这类“苹果和橙子”作比较的把戏。如果你想比较伦敦和巴黎的酒店房间价格，可能会让你6岁大的孩子登录网站搜索—电脑方面你永远不是孩子的对手，然后你的孩子向你汇报巴黎的房价更贵一些，每晚的价格约为180欧元，而相同档次的房间在伦敦每晚只需要150英镑。

此时，或许你会滔滔不绝地向孩子解释英镑和欧元之间的区别，然后让他回去重新查找这两种货币之间的汇率，这样你就能对两个城市的房价作一个有意义的比较。这个例子其实在现实中也挺常见，我的女儿看见我在印度用100卢比买了一壶茶，于是她就问我为什么在印度无论买什么东西都那么贵。显然，在我们将不同国家的货币转换成同一种货币单位之前，比较这些货币上印着的数字是没有意义的。英镑和欧元的汇率是多少？美元和卢比的汇率又是多少？

这似乎是一节痛苦的启蒙课，虽然事实很明显，但却经常被忽略，尤其是政客和好莱坞制片商。这些人当然知道欧元和英镑之间的差别，但就好比苹果和橙子的例子，他们反而会忽略一个更为细微的因素：通货膨胀。今天的1美元和60年前的1美元的价值是不一样的：今天的1美元能买到的东西更少。由于通货膨胀的存在，1950年花1美元能买到的东西在2011年可能要花9.37美元。因此，在没有考虑通货膨胀因素的情况下，任何有关1950年与2011年的金钱比较都是不准确的，而且比欧元与英镑的比较更加离谱儿，因为欧元和英镑的价差比1950年的美元与2011年的美元的价差还小。

经济学家甚至为这一重要的现象冠以专业术语，以表示相关数据是否考虑了通货膨胀因素。名义数据就是没有就通货膨胀做出调整的数字，比较1970年某项政府项目的名义花费与2011年政府在相同项目上的名义花费，实际上看的仅仅是政府财政部在这两年所开出的支票的票面金额，并没有考虑1970年的1美元能买的东西比2011年买到的东西多。假设政府在1970年时为老兵的住房补助项目投入了1 000万美元，到了2011年，政府在此项目上投入了4 000万美元，联邦政府在这个项目上的努力实际上是退步了。花费的金钱在名义上的确是增多了，但这并没有反映出美元价值的变化。1970年的1美元相当于2011年的5.83美元，也就是说，政府2011年需要在老兵的住房补助项目上投入5 830万美元才是与1970年的1 000万美元持平。

实际数据是考虑了通货膨胀因素并做出调整的数字。最常见的方法就是将所有数据统一换算成一个相同的单位，如2011年的美元，这样就可以将“苹果与橙子”之间的比较变为“苹果与苹果”的比较。包括美国劳工统计局在内的许多网站，都提供简易的通胀计算器，供我们对不同时期的美元价值进行比较。下面是一张美国政府最低工资图，上面标出了最低工资的名义值及其实际购买力（都换算成2011年的美元）。通过这张图，我们不难发现考虑了通货膨胀因素并做出调整的数据会产生非常不一样的效果。

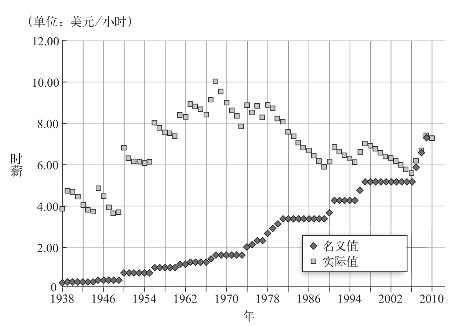
图3–2　美国政府最低工资图

资料来源：http://oregonstate.edu/instruct/anth484/minwage.html(www.xing528.com)

美国最低工资标准是由美国国会制定的。如果你在美国工作，你就会在办公室的某个偏僻角落的公告板上看到最低工资标准。当前的最低工资标准为每小时7.25美元，这是一个名义值。你的上司才不会理会现在的7.25美元能买到的东西是不是和两年前一样多，他只需要保证能够支付给你的时薪不少于7.25美元。上司只跟你谈支票上的数字，而非该数字背后的购买力。

随着时间的推移，通货膨胀会逐渐削弱最低工资的购买力（以及其他名义工资的购买力，这也是为什么工会代表在与雇主谈判时总会谈到“生活成本调整”的问题）。如果商品价格的上涨速度快于美国国会调高最低工资的速度，那么每小时能够获得的最低工资的实际价值就会缩水。最低工资标准的支持者们应该关注这一工资的实际价值，因为这项法律出台的初衷就是为了保护低收入工人的利益，保证他们每小时的劳动所获得的报酬能够换来一定水平的购买力以维持生活，而不是让他们在付出劳动后却得到一张什么都买不起的大额支票。如果这都不能保证，那就相当于给这些低收入工人支付的是卢比，而非美元。

好莱坞在比较不同年份的电影票房时，总是会对通胀因素视而不见，或许是因为无知，但更有可能是出于对利益的考虑。截止到2011年，史上最卖座的5部电影依次为：

1.《阿凡达》（2009）。

2.《泰坦尼克号》（1997）。

3.《蝙蝠侠前传II：暗黑骑士》（2008）。

4.《星球大战IV》（1977）。

5.《怪物史莱克II》（2004）。

这个排名看上去是不是有点奇怪？的确，里面绝大部分的电影都堪称经典，但是，《怪物史莱克II》应该列入其中吗？这部电影真的在票房成绩上要好过《乱世佳人》、《教父》、《大白鲨》吗？当然不是这样的。好莱坞最常做的事就是让最新的大片看上去比上一部的场面更大、更加成功。为达到这个目的，一种方法就是用印度卢比来计算票房成绩，以此来成就令人振奋的报纸头条，如“《哈利·波特》周末票房破1.3万亿卢比，打破票房纪录”。但即使是对金钱最不敏感的某些影迷，也能识破这类用购买力较差的货币统计的“注水”票房成绩。事实上，好莱坞（以及负责媒体电影报道版块的记者）很少用名义数据，因为这一做法会让现在的电影在票房上很轻易地超过10年、20年或者是50年前的电影—谁都知道现在的票价比以前贵多了（当《乱世佳人》在1939年上映的时候，那时美国某地的一张电影票售价只有0.5美元）。比较不同时期电影的商业成功最准确的方法就是，考虑了通货膨胀因素后做出调整的票房成绩。1939年1亿美元的票房可比2011年5亿美元的票房壮观多了。这样来看，将通货膨胀考虑在内，美国史上最卖座的5部电影到底是哪些？

1.《乱世佳人》（1939）。

2.《星球大战IV》（1977）。

3.《音乐之声》（1965）。

4.《外星人E·T》（1982）。

5.《十诫》（1956）。

以剔除通胀因素的实际票房成绩来看，《阿凡达》只排到了第14位，《怪物史莱克II》则落到了第31位。

有的时候即使是拿苹果与苹果进行比较，也可以毫不费力地欺骗他人。上一章的内容里曾经讲过，统计学的一个重要角色就是描述数量随着时间推移所发生的变化。我们缴的税是不是越来越多？与2012年相比，2013年的汉堡销量如何？饮用水中的砷含量到底降低了多少？我们经常使用百分率来描述这些变化，因为百分率能够让我们相对直观地有一个比例和背景的感受。很多人会理解饮用水中的砷含量降低了22%是什么意思，但能感知每一单位水中减少1微克砷（绝对减少量）到底是多是少的人就没几个了。百分率不会撒谎，但它们会夸大其辞。让增长出现“爆炸”的方法之一就是与一个非常低的起点进行百分率比较。我住在伊利诺伊州的库克郡，一天我得知我缴纳的税款中用于支持库克郡郊区肺结核疗养院的比例上升了527%！我着实吃了一惊。愤怒的我马上开始筹划一场大型的抗税集会，而就在此时，我才知道这一变化给我增加的负担还不够一个火鸡三文治的钱。肺结核疗养院每年接收的病人才100多例，并不是一个规模庞大或昂贵的机构。据《芝加哥太阳报》报道，对于一个普通家庭来说，其支付的税额仅仅是从1.15美元上升到了6美元。研究人员有时候会特别指出某项增长数据是由“一个较低的基数”得出的，哪怕是很小的一点儿增长在进行百分率比较时，看上去都会很可观。

除此之外，百分率的另一面也是很可怕的，那就是一个庞大数额的微小比例也会是一个很大的数字。如果美国国防部部长说，2013年的军费开支仅增长4%—这看上去可是一条好消息啊！作为纳税人的我们，是不是应该庆祝？其实并不尽然，因为美国的国防预算是在7 000亿美元左右，4%的比例就是280亿美元，这笔钱能买多少个火鸡三文治啊！事实上，区区4%的军费开支就已经超过了美国国家航空航天局（NASA）的全部预算，相当于美国劳工部和财政部预算的总和。

同样的，想象一下你有一个菩萨心肠的老板，出于公平的考虑，他决定2013年为公司的每一位员工加薪10%—多么慷慨的决定啊！只不过有一点，老板的年薪是100万美元，而你每年只挣5万美元，老板将会得到10万美元的加薪，而你只有0.5万美元的加薪。“2013年每个人都将获得10%的加薪”听上去要比“我的加薪是你的20倍”好受太多了—虽然这两句话都没错。

只要是对一段时间内的数字变化进行比较，就肯定离不开一个起点和一个终点，但我们有时候能通过操纵这些点来影响信息的表达。曾经有一个教我的教授，他对美国共和党和民主党操纵数据的伎俩十分清楚，尤其是在军费开支的问题上，他指出就算是面对完全相同的数据，不同的分析方法也能够产生不同的效果，既可以用来取悦民主党的支持者，也不会让共和党的拥护者失望。因此，在准备课件时他会做两个版本的幻灯片，当为共和党人上课时，就拿出“共和党版”的课件，为民主党人上课时，自然就会换成“民主党版”的课件，但里面的数据是完全相同的，不同的只是组织数据的方式。就比如今天的这节课他的听众主要是共和党人，他的幻灯片上就会出现下面有关罗纳德·里根（共和党人）总统执政期间的军费开支统计图。大家都清楚里根为美国赢得了冷战，对国防安全做出了卓越贡献。在看着这些数字的时候，无人不为里根总统处理政务时所表现出的钢铁般的决心击掌喝彩。

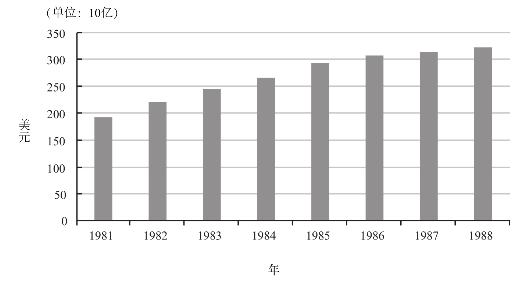
图3–3　美国军费开支，1981～1988年

面对美国民主党人时，我的这位教授还是用相同的（名义）数据，但在时间跨度上稍长一些。他对这群听众指出，吉米·卡特（民主党人）总统是开启国防建设的当之无愧的先驱。正如下面的这张“民主党版”的幻灯片所示，卡特掌权的1977～1980年间，美国的军费增长趋势与继任的里根总统大同小异，感谢上帝让来自安纳波利斯的前海军军官吉米·卡特带领美国走上了军事自强之路！

图3–4　美国军费开支，1977～1988年

资料来源：http://www.usgovernmentspending.com/spend.php?span=usgs302＆year=1988＆view=1＆ex pand=30＆expandC=＆units=b＆fy=fy12＆local=s＆state=US＆pie=#usgs302

虽然统计学的要点在于为我们所关心的事物描绘一幅有意义的画面，但是在许多时候我们同样希望能够为这些数字做些什么。美国职业橄榄球联盟的球队希望获得四分卫成绩的简单统计，这样他们就能在众多大学生中寻找到天才球员；企业通过考核指标来提拔那些有价值的员工、开除那些纯粹混日子的人。在商界流传着一句至理名言：“你无法管理你无法衡量的事物”。这句话千真万确，但你最好要保证你所衡量的，正是你努力想去管理的。

谈到学校的质量，这是一个必须予以衡量的关键问题，因为我们都希望奖励并效仿“好”学校，惩罚或整顿“差”学校（具体到学校内部，我们在衡量教师的教学水平问题上也面临类似的难题）。考核学校和教师最常用的方法就是看学生的考试分数，统考结束后，学生的优异成绩就是教师和学校最好的金字招牌；与之相反的，糟糕的成绩无疑会释放出一个清晰的信号：相关教师应该被辞退，而且越早辞退越好。这样看来，仅凭考试分数我们就能彻底改善公共教育系统了，对吗？

错。在评价教师和学校时，如果只看考试分数是会铸成大错的。不同学校的学生，他们的背景和能力是很不一样的，比如说，学生父母的教育程度和收入会对孩子的成绩产生不可忽视的影响，不论孩子上的是哪所学校。在这里，我们所缺少的那个数据恰好就是解答这个问题唯一需要的：学生的学业表现有好有差，但其中有多少比例要归功或归咎于学校（或所在的班级）呢？

从小就生活在衣食无忧、书香门第家庭里的孩子，一般来说从进入幼儿园的第一天起就有可能会比别的孩子的成绩好。相反的情况同样成立，有些学校的学生天资平平，虽然教师教得很好，但是学生的成绩还是处在一个低水平上，如果没有这些老师的付出，那些学生的成绩会更加惨不忍睹。所以，我们需要在学校，甚至班级层面上将一些“附加值”纳入考核。学生成绩的绝对水平对于解答我们的问题没有意义，我们想知道的是这些学生的表现中有多少是受到了学校和教师的影响，我们想要评估的其实是这些教学因素。

有人会说这并不难，只需要在开学时给学生安排一场摸底考试即可，再将这次考试的成绩与入学之后的考试成绩进行对比，就能够判断学生的学业是进步了还是退步了，并由此对其所在的学校或班级进行评价。

但这种方法还是错误的。不同能力或背景的学生在学习上的进步程度也是不同的。一些学生在领会知识点方面就是比其他学生快，而这与老师的教学质量没有关系。假如让优质学校A的学生和各方面都稍差的学校B的学生同时开始学习相同难度的代数课，一年以后，A校学生的代数成绩更理想，原因可能是A校的教师教学能力更强，也可能是A校学生的学习能力更强，还有可能二者兼有。研究人员正在致力于开发一套针对不同能力和背景的学生的教学质量统计评价方法，在此期间，我们所有关于寻找“最佳”学校的努力都有可能适得其反，误导大众。

每年秋天，芝加哥的几家当地报纸和杂志都会对该区域内的高中进行一次排名，其主要参考依据通常是州考成绩。从统计学的角度看，这些排名难免会有一些让人捧腹的地方，比如常年位居榜单前几位的都是一些选择性招生的学校，意思是说学生要进入这些高中，就必须提出申请，申请者中只有很小一部分的人能够如愿，而这些学校在挑选学生时最重要的参考依据就是学生的统考成绩。我们就这个问题作个小结：（1）这些学校因其学生在州考中的出色发挥而被认为是“优质”学校；（2）要进入这些学校学习，首先学生要有非常高的考试分数。这一逻辑就好比是给一支篮球队颁奖，理由是这支篮球队的训练在促进学生长高方面贡献卓著。

面对你想要衡量和管理的对象，就算你找到了一个有效的评价指标，挑战也并未结束。好消息是“用统计学进行管理”能够让相关个人或组织的潜在行为往好的方向改变。如果能够计算出一条生产线上生产出的产品的不合格率，而且这些不合格产品是由组装工人自身的原因造成的，那么对那些生产出的产品不合格率低的工人给予某些奖励，能够在一定程度上激励全厂工人积极工作的态度，这就是一个统计学优化工作的例子。无论是谁，都不会对激励措施（哪怕仅仅是几句赞扬或一个地段好一点的停车位）无动于衷的。统计学帮我们得到重要的结果，激励措施给我们改善结果的理由。

坏消息则是，在某些时候，统计学的功能仅仅是让数据看上去更顺眼。

如果某个高中是根据其毕业生占所在学区毕业学生总数的比例来评估校领导的能力，甚至是奖金分配方案，那么这些领导们的工作重心肯定会放在提高学生的毕业人数方面。当然，他们或许也会抽出一点精力放在提升本校学生的毕业率，但归根结底毕业人数和毕业率并不是一回事。例如，还没毕业就离校的学生可以被归类为“转校”而不是“辍学”。这不是一个虚构的例子，美国教育部前部长罗德·佩奇就是因为这个问题而备受指责。美国前总统小布什之所以提名佩奇掌管美国教育部，就是因为他成功地降低了休斯敦地区的学生辍学率、提高了学生的考试分数。

如果你一直默默地记下我引用的为数不多的商业警句，那么请在笔记本上写下这么一句话：“当《60分钟》电视新闻杂志栏目剧组敲你家门的时候，肯定没有什么好事。”之前丹·拉瑟和《60分钟》栏目组专门去了一趟休斯敦，发现教育部对统计数据的操纵远远超过了教育水平的提升。将辍学的学生归类为转学、出国或攻读一般同等学力（GED）文凭，在当地高中是一个极为普遍的现象，在官方的统计数据中，这些学生都不会被统计到辍学率中。休斯敦市公布的辍学率为1.5%，而《60分钟》栏目组暗访计算出的实际辍学率为25%～50%。

在考试分数的统计过程中，也出现了同样恶劣的作弊现象。在休斯敦（或是其他任何一个城市），提高考试成绩的方式之一就是改善教学质量，这样学生就能学到更多的知识，并且在考试中取得进步，改善教学质量确实是较好的方法。而比较差的方法则是想办法让那些成绩最差的学生“远离”考场，即使剩余参加考试的学生的成绩没有任何长进，最终考试的平均成绩也会有所提升。在得克萨斯州，10年级学生需要参加全州统考，有证据表明休斯敦的中学有意让学习能力较差的学生留级，不让他们升为10年级生。休斯敦曾曝出过一个令人震惊的事情：一个学生连续3年当9年级生，然后直接升到了11年级—通过这样一种狡猾的运作，既能让一个成绩较差的学生免于在10年级统考中使总体分数下滑，又不至于让他因辍学而影响到升学率。

罗德·佩奇到底有没有在他的任期内参与策划这些操纵统计数字阴谋，我们并不清楚，但有一点是肯定的，他曾颁布了一个严格的问责政策，用以奖励那些达到升学率目标和考试分数目标的学校校长，同时对那些没能达标的校长予以解聘或降职处理。可想而知，整个休斯敦的校长们必然会积极响应，在这堂“课”上他们可不愿落后。但我们必须清醒地认识到，要想在评估报告上大放异彩，这些校长必须时刻将目标放在心中，任何与其有冲突的管理方法都不会有好下场。

纽约州就因为类似的统计陷阱而栽了大跟头，付出了惨痛的代价。州政府之前出台了“记分卡”制度，对接受心脏搭桥手术的病人的死亡率进行统计，以便让公众在选择心脏科医生时有一个参考。这似乎是一个完全合情合理，而且有所帮助的描述统计学在政策制定过程中的应用。心脏搭桥手术是治疗心脏病最常用和有效的方法，心脏病人在搭桥手术过程中的死亡比例当然是一个非常重要的数据，而作为个人根本没有办法了解到确切数据，因此政府出面收集并向公众公开这一数据是合乎情理的。但就是这么一个“好”政策，却导致了更多病人的死亡。

心脏科医生肯定会在意他们的“记分卡”。但是对于一个外科医生来说，降低病人死亡率最简单的方法并不是降低病患死亡人数，因为大部分医生在救死扶伤方面已经竭尽全力了。降低死亡率最简单易行的方法是拒绝为那些病况最严重的病人动手术。罗彻斯特大学医学与牙医学院的一项调查表明，以服务病人为初衷的记分卡，到头来反而会给病人造成伤害：在参与调查的心脏科医生中，有83%的医生表示正是由于公开了死亡率数据，一些本来可以从搭桥手术中获益的病人最终没能被安排进行手术；79%的医生表示收集并公开死亡率数据或多或少地影响了他们的治疗决策。这一看似有用的描述性数据存在一个可悲的矛盾，而心脏科医生也只能理性地接受并采取自己的对策，就是让那些最需要心脏搭桥的病人远离手术台。

作为一个统计指标，不仅时常会“携带”其他描述性数据可能存在的陷阱，而且就其自身而言，将许多指标数据融合为一个单一的数字，这多少都会对现实和真相产生扭曲。从定义来看，任何一个指数对其构成都是十分敏感的；无论是所采用的指标数据的变化，还是各个数据的权重变化，都会对指数的最终呈现产生影响。举例而言，为什么美国国家美式橄榄球大联盟（NFL）在计算传球效绩指数时不将第三次触地完成率考虑在内？在计算某个国家的人类发展指数时，识字率和人均收入两者的权重该如何确定？最终，我们必须面对的重要问题就是，如果计算过程的不准确性无法克服，那么花那么大气力将众多数据压缩成一个数字就只是为了简单和易于使用，这一切是否值得？有些时候，这样做的确不值得，就比如（我们之前提到的）《美国新闻与世界报道》的大学排名。

这份排名动用了16个统计指标为美国的学院、大学和专业院校打分、排名。以2010年为例，在为综合性大学和文理学院排名的过程中，“录取新生”占15%。基于大学录取率的“录取新生”指标，是指所录取学生中成绩占其所在高中年级前10%的学生的比例，以及录取学生的SAT和ACT（美国大学录取考试）的平均分。《美国新闻与世界报道》刊登大学排名的好处在于，这份榜单以一种简单易懂的方式囊括了全美几千所大学的海量信息，就连其批评者们也承认，其中收集的有关美国大学的很多信息都是有价值的。许多有远见的学生都会想要知道心仪大学的毕业率和班级平均规模。

当然，提供有意义的信息与将这些信息浓缩成一个权威排名完全是两码事。在批评家的眼里，这份排名设计粗糙、误人子弟、对高中毕业生的长远发展有百害而无一利。“问题之一就在于将教育机构以数字顺序进行排名，而原始数据本身并不支持如此精确的操作。”明尼苏达州麦卡利斯特学院前校长迈克尔·麦弗逊说。凭什么“校友捐赠”要占学校综合得分的5%？如果这项指标真的很重要，那么为什么不干脆占10%的比例？

按照《美国新闻与世界报道》的说法，“每一项指标都存在一个权重（表现为百分比的形式），我们会根据这些指标的重要程度来判断不同指标的权重大小。”可是，有时候判断和专断的界线就是那么模糊。在这个美国高等院校的排名系统中，权重最大的指标是“学术名誉”，该指标是基于其他院校的负责人所填写的一份“同行评估调查”以及高中升学指导员的调查统计得出的。马尔科姆·格雷德威尔向来对排名持怀疑的态度，大学排名更是他猛烈抨击的对象，特别是同行评估法，在他看来就是一个笑话。马尔科姆·格雷德威尔举了一个例子，密歇根最高法院的一位已经退休的大法官曾经向100多位律师寄发了一份问卷，让他们选出心目中最好的10所法学院。宾夕法尼亚州州立大学法学院的名字也出现这份问卷上，其最后的统计排名结果是宾夕法尼亚州州立大学法学院的教学质量居中等偏下。但问题出现了，在那个时候，宾夕法尼亚州州立大学法学院还没有成立。

面对《美国新闻与世界报道》收集的所有数据，我们不知道这些排名到底是想给那些即将跨入大学校门的高中毕业生们哪方面的指导。站在学生的立场，最值得关注的方面应该是学业本身：如果我申请了这所大学，我能在学业上获得怎样的帮助？橄榄球迷聚在一起时经常会抱怨传球效绩指数的构成，但却没有人否认其组成部分—完成率、码数、触地得分和截球—同样是评估一名四分卫的整体表现不可或缺的重要参考。但回到大学排名上来，情况就完全不同了。《美国新闻与世界报道》过于强调“输入”（例如，录取了哪些学生、教职员工的薪资待遇、全职教授所占的比例等），反而忽略了教学“输出”，除了仅有的两个例外—新生留级率和毕业率，但实际上就连这两个指标也不是衡量教学质量的。正如迈克尔·麦弗逊所指出的：“从这份排名中，我们无从知晓进入某所大学经过4年的学习之后，学生的能力是否提高了，他们的知识是否增长了。”

虽然大学排名看上去是一些无伤大雅的统计数据，但事实上，它会导致一些对学生或高等教育无益的行为。举例说明，用以计算排名的数据之一就是每个学生能够获得的资助，可这些钱花得值不值得，排名中却没有一个相应的衡量数据。那些花更少的钱却给予学生更好的教育（因此学费也会低很多）的大学，却在排名中体现不出优势。此外，高等院校都希望申请本校的学生人数越多越好，包括那些根本没有任何希望的学生，因为这可以让它们变得非常热门，有助于提升自己的排名。但提高排名无论对学校还是对学生都是一种浪费，学校方面要花大量精力来吸引学生，而大部分学生到最后发现自己做的也是无用功。

鉴于下一章的内容与概率有关，因此我不妨在此打一个赌：《美国新闻与世界报道》的大学排名时日不多了。巴德学院的院长利昂·波特斯坦说得很精辟：“人们喜欢看到简单的答案。什么是最好的？当然是第一名。”

本章内容一直在强调，统计陷阱与数学能力的关系不大。哪怕是令人叹为观止的精确计算也会混淆视听，甚至成为不良动机的掩护。有时候哪怕你准确无误地计算出平均数，也无法改变中位数在对真相的描述中更加准确这样一个事实。判断和正直成为关键所在，就好比一个人非常懂法也不能阻止其犯下罪行一样。渊博的统计学知识无法遏制不道德的行为，无论是统计学还是法律，坏人总是清楚地知道自己在做什么！