如何确定数据的集中趋势？

Naked Statistics

你一直想买的一条连衣裙，商场售价为4 999元，先降价25%后再提价25%，你能算出这条连衣裙的最终售价是多少吗？

让我们先来思考两个看上去毫不相干的问题：（1）美国中产阶级的经济健康状况出了什么问题？（2）谁是有史以来最伟大的棒球运动员？

第一个问题极为重要，几乎构成了每次美国总统选举和社会运动的核心。中产阶级是美国的心脏，这一群体的经济状况是整个国家经济运行健康与否的关键性指标。相比之下，第二个问题就显得微不足道了，但棒球爱好者或许会持有不同的意见。这两个问题的共同之处就在于，当谈到运用数字和数字运算来总结原始数据的描述统计学时，它们都能用来说明其优点和局限所在。

如果我想证明德瑞克·基特是一位多么伟大的棒球手，我可以先让你坐下，然后向你娓娓道来基特在每场职业联盟比赛中的每一次击球，这就是原始数据，而且你需要花很长一段时间来消化，因为基特为纽约洋基队效力了17个赛季，上场击球的次数累计达到了9 868次。

或许我也可以告诉你，在2011赛季结束的时候，德瑞克·基特的击球率为0.313，这是一个描述性数据，即一个“统计量”。

显而易见，击球率是对基特参加的所有17个赛季的简化统计，不仅易于理解，而且简单，但所能传达的信息却十分有限。棒球运动专家们的手中还有很多在他们看来比击球率更有价值的描述性数据。史蒂夫·莫耶是一家为客户提供大量原始数据的棒球信息解决方案公司的老总，之前我与他通了电话，特地向他咨询了几个问题：（1）哪些是评价棒球天才最重要的数据？（2）谁是史上最伟大的棒球手？在介绍完背景之后，我会向大家公布莫耶的答案。

现在让我们回到那个更加重要的问题上来，谈谈美国中产阶级的经济健康状况。当然如果我们能够找到类似于击球率这样言简意赅的，甚至更好的经济衡量指标，那是最理想的，我们需要一个简单且准确的数字，来说明一个典型的美国工人最近几年的经济状况，那些我们称之为“中产阶级”的人到底是更富了、更穷了，还是在原地踏步？一个合理的答案—肯定不会有“正确”的答案—就是，计算一代美国人（大约为30年）的人均收入，观察其变化趋势。人均收入是一个简单的平均数：总收入除以人口数，这样得出的结果就是美国的人均年收入从1980年的7 787美元上升到2010年的26 487美元。你看，真是一个值得庆祝的成就！

但只有一个小问题，我的计算方法在技术上是正确的，但是对于我一开始提出的那个问题来说，却是完全错误的。首先，上面的数据没有考虑通货膨胀因素，1980年的7 787美元相当于2010年的约19 600美元。但仅进行通货膨胀因素的处理还不够，更大的问题是，我们需要知道的是普通美国人的收入，而不是泛泛的人均收入，这两者有本质上的区别。

人均收入仅仅是将整个国家所有人的收入加起来再除以总人口数，我们无法从这个计算结果中得知各阶级收入所占的比例，无论是1980年还是2010年。正如“占领华尔街”运动的示威者所指出的，处于收入排行榜顶端的那1%的人，他们收入的爆炸性增长能够显著地拉动人均收入水平的整体提升，但同时不需要往剩下的那99%的人的口袋里多放一分钱。也就是说，在普通美国人的生活陷入水深火热的同时，美国的人均收入依然能够节节攀升。

与之前有关棒球的问题一样，这次我又请教了专家，咨询我们应该如何看待美国中产阶级的经济问题。我找到了两位知名的劳动经济专家，其中包括美国总统奥巴马的高级经济顾问，询问他们会采用哪些描述性数据来评价一个典型美国人的经济状况是否良好。是的，作为读者，你也会读到他们的答案，不过在那之前，我们还是要对描述统计学有一个大体的认识，这样才能更好地理解专家的观点。

从棒球到收入，对大量信息进行归纳是处理数据时最基本的任务。美国有3.3亿名居民，一张记录每位美国人的姓名和收入的电子表格包含了我们衡量这个国家经济健康状况所需的所有信息，但这张信息过量的表格其实相当于什么都没有告诉我们。这就是让人觉得讽刺的地方：经常是数据越多，事实越模糊。因此，我们需要简化，将一系列复杂的数据序列减少为几个能够起到描述作用的数字，正如奥运会体操比赛中，我们将一套多难度组合的复杂动作浓缩为一个得分：9.8。

好消息是，这些描述性数据为我们提供了一个针对某一现象的可操作、有意义的概括，这也是本章所要讲的。但坏消息是，任何一种简化都会面临被滥用的危险。描述性数据就像是在线交友网站上的档案：虽然每一条都是准确的，但同时也相当具有误导性。

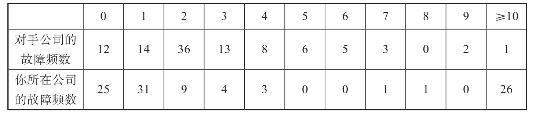
假设你在上班，此刻正无所事事地浏览网站，无意间你浏览了一篇报道，是关于美国娱乐界名媛金·卡戴珊和职业棒球手克里斯·亨弗里斯的感情生活的，这篇报道里详细记录了他们两个人72天“短命”婚姻的点点滴滴。你正津津有味地看到他们结婚第7天的生活时，你的老板手里拿着两份厚厚的文件出现在你的办公桌前。其中一份文件包含了你所在公司前一年售出的57 334台激光打印机的保修信息（每售出一台打印机，文件中都会记录下这台打印机保修期内的质量问题和返修次数）；另一份文件记录了公司最主要的竞争对手在前一年售出的994 773台激光打印机的保修信息。老板想让你对两家公司的打印机质量作一个对比。

幸运的是，你用来阅读卡戴珊婚姻生活报道的这台电脑里恰好安装了基本统计软件包，但应该从哪里入手呢？听从直觉的召唤一般来说总是没错的：描述任务的第一步通常是估量某套数据的“中间位置”，也就是统计学家所说的“集中趋势”。在比较的过程中，你所在公司打印机的质量体验总体如何？对于数据分布的“中间位置”，最基本的估量方法就是求平均数，具体到这个案例，我们需要知道你的公司和竞争对手公司平均每台打印机的质量问题分别有多少个。简单来说，你先数出保修期内所有记录在案的质量问题，再除以打印机的销售总数就可以了（相同的一台打印机在保修期内可能会出现多个质量问题）。之后再算出另一家公司的数据，这样就能得出一个重要的描述性数据：已售打印机的平均质量问题数。

假设竞争对手售出的打印机在保修期内平均每台反馈的质量问题数为2.8个，而你的公司所售打印机的平均质量问题数为9.1个，这样说够直白了吧？通过计算，两家公司共计100多万台打印机的信息就被你提炼浓缩为问题的核心所在：你公司的打印机经常出现问题。现在你就可以给你的老板发一封简短的邮件，用数据告诉他两家公司打印机的质量差距，然后点开之前的网页继续看那位名媛金·卡戴珊婚后第8天的生活。

或者，你也可以等会儿再浏览网页。刚才谈到数据分布的“中间位置”时我并没有展开，其实所谓的平均数、平均值在这里是有一些问题的，即它们容易受到远离中心区域的“异常值”的干扰而出现失真。为了能够让大家更好地理解，我来举个例子，在西雅图的一家中档酒吧的吧台前，坐着10个人，他们每年的平均收入都是3.5万美元，也就是说，这组人的人均年收入为3.5万美元。这时候，比尔·盖茨走进了这家酒吧，肩膀上立着一只会说话的鹦鹉（其实这只鹦鹉与这个事例一点儿关系都没有，之所以要提一下鹦鹉是想给这个案例增加点儿乐趣），假设他在这个案例中的年收入为10亿美元。当比尔·盖茨在吧台前的第11把凳子上坐下后，这组人的平均年收入便迅速上升到了将近9 100万美元。很显然，之前的那10个人丝毫没有变得更富有（尽管比尔·盖茨很有可能会帮他们付一两次酒账，但仅此而已）。如果我说吧台前的这群人平均年收入为9 100万美元，这句话在数据上是正确的，但同时也相当具有误导性。这里不是一个亿万富翁会经常光顾的酒吧，只不过正好有一群收入不高的普通人坐在了比尔·盖茨和他的会说话的鹦鹉旁边。平均数必须对“异常值”有足够的敏感性，这也是为什么我们不应该用人均收入来衡量美国中产阶级的经济健康状况。因为在收入分配的顶端，有着一群收入暴涨的美国人—公司高管、对冲基金经理，以及像德瑞克·基特这样的运动员，普通美国人的收入会被这些巨富们的光环掩盖，就像一群失意的普通人坐在比尔·盖茨身边一样。

出于这个原因，我们还有一个数据可以用来表示分配的“中间位置”，但与平均数有所不同，这个中间位置就是中位数。中位数正好将一组数字一分为二，1/2位于中位数之前，另外1/2位于中位数之后（如果遇上一组数字的数量为偶数，那么中位数就是中间两个数的平均值）。回到刚刚酒吧的那个例子，原先坐在吧台前的10个人的年均收入中位数为3.5万美元，当比尔·盖茨和他的鹦鹉入座之后，这11个人的年收入中位数依然为3.5万美元。如果你将他们按照收入多少来排座的话，那么坐在第6把凳子上的人的收入就代表了整组人收入的中位数。假如此时沃伦·巴菲特走了进来并坐在了比尔·盖茨的身边，他们的中位数还是不会改变。^[1]

如果一组数据分布中没有特别离谱的异常值，那么它们的中位数和平均数将会是差不多的。下图中，我模拟了一张对手公司打印机质量数据的统计图，需要特别注意的是，我列出了“频数分布”的数据。每台打印机出现质量问题的次数被依次排列在X轴上，每根柱子的高度代表售出的这批打印机中出现相应数量质量问题的打印机占总数的百分比，即Y轴上的频数，例如，在保修期内，36%的打印机出现过两次质量问题。这一数据分布涵盖了所有可能出现的质量问题的数量，包括零故障，因此所有频数相加的结果肯定等于1（或100%）。

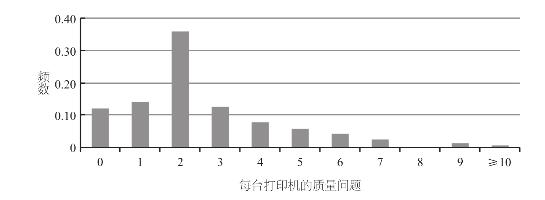
图2–1　对手公司打印机质量问题频数分布

由于上图的数据分布情况基本上是对称的，因此平均数和中位数两者相对接近。坐标轴的右边还有一小部分故障数量较多的打印机，这些异常值将会拉高平均数，但是对中位数没有影响。假如在你准备将质量统计结果发给老板之前，你决定对两家公司打印机的质量问题求一下中位数，在敲击几下键盘之后，你得出了结果。对手公司的质量投诉中位数为2，而你所在公司的这一数字则为1。

你瞧怎么样？你所在公司每台打印机的质量问题的中位数实际上要小于对手公司。此时，由于卡戴珊的婚姻生活已经开始变得枯燥乏味，而且你也深深地被你刚才的发现所吸引，于是你忍不住为自己公司的质量问题画了一张频数分布图。

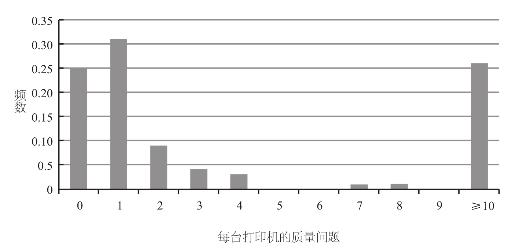
图2–2　你所在公司打印机质量问题频数分布

从图中可以清楚地看到，你所在公司的产品并不存在一个普遍的质量问题，但却有一个棘手的麻烦：一些数量不多的打印机存在大量的质量问题。这些异常值抬高了质量问题的平均数，但没有对其中位数造成影响。从生产的角度看，更为重要的一点是，公司无须更新或重组整个生产流程或生产设备，唯一需要做的就是调查这批问题很多的劣质打印机，找出源头并予以解决。

无论是中位数还是平均数，要求出它们并不难，关键在于根据具体情况确定哪一个“中间位置”能够更准确地反映问题的实质。与此同时，中位数还有一些有用的“亲戚”，正如我们之前已经讨论过的，中位数将一组数据从中间分为两部分，这组数据其实还可以继续分为4部分，我们称之为“四分位数”。第一四分位数由处于底部的25%的数据构成，往后的25%的数据构成了第二四分位数，以此类推。同样的，收入分配数据还可以分为“十分位数”，每组包含10%的数据。如果你的收入属于美国人均收入分配顶层的那10%，那么这意味着你要比90%的美国人挣得都多。我们还可以细分下去，将收入数据分为100份，也就是“百分位数”，每个百分位数都代表1%的数据，也就是说，第一百分位数表示位于底部的1%的人的收入，第99百分位数代表收入分配数据中收入最高的那1%的人。

这类描述性数字的好处在于，它们描述了某个具体的值在与其他数据进行比较时所处的位置。如果我告诉你，你的孩子在阅读考试中的成绩处于班级的第三百分位数（有97%的孩子的分数比你的孩子高），你该即刻意识到全家人应该在学习方面多辅导孩子。你没必要知道任何有关考试本身的内容，以及你的孩子在考试中答对了多少道题目。一个以百分位数显示的成绩就已经告诉你，你的孩子的得分在所有考生中的排名。如果考试题目比较简单，那么大多数考生都会获得一个高分，而你的孩子答对的题目数量还是少于其他同学；如果考试题目特别难，那么所有考生的正确率都不会高，而你的孩子的答题正确率比其他孩子要更低一些。

现在我来穿插介绍几个有用的统计术语。一个“绝对”分数、号码或数字具有一些与生俱来的意义，比如，我在一场18洞高尔夫球比赛中打出了83杆，这就是一个绝对分数；或许那天的气温正好是14摄氏度，这也是一个绝对数字。通常来说，在没有任何背景或额外信息的前提下，绝对数字依然能被理解。当我告诉你我在18洞高尔夫球比赛中的成绩是83杆的时候，你不需要知道其他高尔夫球球员取得的成绩，就可以对我的表现给出一个评价（除非那天的环境极为恶劣，又或者场地条件有所限制）。又比如，在一场高尔夫球锦标赛中我的排名是第9位，这是一个相对数据。一个“相对”值或数字只有在比较或处于一个更大的背景中时才有意义，比如说有8位球手在比赛中发挥得比我出色。绝大多数的标准化考试给出的结果都只具有相对意义，如果我告诉你伊利诺伊州某小学的一个三年级学生在满分为60分的州考数学考试中的成绩是43分，这一绝对分数并没有太多的意义。但是，当我将其转换为一个百分位数，也就是将这一原始分数代入全伊利诺伊州所有三年级学生的数学成绩中作对比，那么含义将会得到大大的丰富。如果43分的成绩处于第83百分位数，就代表这个学生的成绩要优于全州大部分的同龄人。如果他处于第8百分位数的位置，那么他真的要加点儿油了。在这个例子中，百分位数（相对分数）比答对题目的数量（绝对分数）要更有意义。

标准差也是一个能够帮助我们在一大堆杂乱无章的数字中发现真理的统计数值，我们用它来衡量数据相对于平均值的分散程度。根据标准差，我们可以知道所观察数值的分散情况。如果我要收集某班飞往波士顿的航班上的250名乘客的体重数据，还有250名有资格参加波士顿马拉松比赛的运动员的体重，假设这两组人的平均体重差不多都是155磅（约为70.3千克）。任何一个曾经在拥挤不堪的飞机里费劲地挤进自己座位和争抢扶手的人都清楚，一架典型的商用客机上有许多人的体重都超过155磅，但同时你或许也能回忆起在这些乱哄哄、人挤人的航班上还有不少啼哭的婴儿和不听话的孩子，他们的肺活量不小，但是体重就很轻了。在计算航班上乘客的平均体重时，尽管坐在你身边的足球运动员有高达320磅的体重，但平均体重仍有可能被前排正在尖叫的婴儿和后排正在踢你座椅靠背的6岁小孩的体重拉低。

目前为止，用我们所学的描述统计学的工具来看，航班乘客和马拉松运动员的体重几乎是相等的，但事实并非如此。是的，两组人的体重有着相差无几的平均数，但是航班乘客的体重距离平均数的标准差要远大于马拉松运动员，也就是说前者的体重分布要更加分散。连我8岁大的儿子都会说，马拉松运动员们的体重看上去都差不多，但飞机上的乘客就很难说了，有抱在怀里的婴儿，也有胖得离谱儿的人。航班乘客们的体重“更加分散”，这是在形容两组人的体重时需要提到的一个重要特征。标准差这一描述性数据能够让我们用一个独立的数字来表示距离平均数的离散程度。用于计算标准差和方差（另一个由标准差推导而来的用于衡量离散程度的指标）的公式在本章后面的内容中可以找到。现在，首先让我们来谈谈衡量离散程度的重要性。

我们再来作一个情景假设。自从被提拔为北美地区打印机产品的质量总监后，你就一直倍感疲惫，于是你决定去看医生。医生给你验了血，几天后他的助手在你的电话答录机上留言，告知你的HCb2值（一个虚构的血液指标）为134。你立刻打开电脑，搜索你这个年纪的人的HCb2平均值是多少，结果网页上显示是122（而且中位数也几乎是这个值）。我的天！如果换作我，我可能就要开始写遗嘱了，然后噙满泪水地给我的父母、爱人、孩子和挚友们写告别信。做完这些之后，我会想想自己还有什么未完成的心愿。我要去跳一次伞，还要用我余下的时间写一部小说。最后，我还要写一封令人声泪俱下的控诉信给我的老板，用恶狠狠的措辞把这几年在他那里受的气都发泄出来—而且从头到尾都要用大写的英文！

然而，上面这些事情中没有一件是必要的（那封发给老板的信带来的后果可能会很严重）。当你回拨医生的电话，打算安排你的临终事宜时，他的助理告诉你，你的指标在正常范围内。但这怎么可能呢？“我的HCb2值比平均值足足高出12！”你不断地跟电话那头的人重复着这句话。

“HCb2值的标准差是18。”对方淡淡地说了一句。

这又是什么？

HCb2值与其他大多数生理现象（如身高）一样，都存在天然差异。尽管这一虚构指标的平均值为122，但大多数健康的人体检时得到的结果都会有高有低，只有在HCb2值特别高或特别低时才会对健康构成威胁。那么，对于HCb2值来说，上下浮动多少才算是数值异常呢？正如我们之前提到的，标准差是衡量离散的指标，反映了分散在平均值周围的数据的聚合程度。对于许多典型的数据分布来说，有很大比例的数值都位于它们的平均数的某个标准差范围以内，也就是说，这些数值有的比平均值大，有的比平均值小，但都是在一个正常范围之内的。举个简单的例子，美国成年男性的平均身高为70英寸（1.778米），标准差约为3英寸（0.076 2米），这意味着有很大一部分美国成年男性的身高在67英寸（约1.7米）到73英寸（约1.85米）之间。

换言之，任何一个身高介于上述区间内的美国成年男性都不会被认为身高异常。让我们再回到刚刚那个困扰你的HCb2的问题上。是的，你的指标是比平均值高了12个数值，但还没有超过标准差范围，这就好比你的身高为72英寸一样—这没有什么好奇怪的。当然，距离平均值两个标准差的数值会减少，3～4个标准差的数值就更少了。以身高为例，如果一个美国成年男性高于平均身高3个标准差，那么他的身高至少为79英寸（约2米多）。

不同群体对象的数据分布的离散情况是不同的。可以这么说，航班上250名乘客体重的标准差要比250名马拉松运动员的大，如果将两组人的体重数据画成频数分布图的话，前者肯定要比后者更“胖”（分散）。对于任何一组数据来说，只要知道了平均数和标准差，我们就能进行简单的统计学分析，得出一些可以信赖的结论。比如，我告诉你美国SAT数学考试的平均分为500分，标准差为100，与身高的例子一样，大部分参加考试的学生的成绩都会在一个标准差范围内浮动，比如400～600分。那么，你觉得又有多少名学生的成绩会高于720分呢？估计不会有很多，因为这比平均分高出两个标准差还要多。

事实上，我们能做的不仅只是“学生人数不会有很多”这样的回答。现在就向大家隆重介绍统计学里最重要、最有用、最常见的分布之一：正态分布。数据的分布一般来说都是对称的，以平均数为中轴呈现类似于“钟”的形状，我想大家对此应该不会感到陌生。

正态分布可用于描述许多常见的现象。如果我们要给爆米花的“爆炸”过程画一张频数分布图，那么分布图的情况应该是：一开始的时候只有少量玉米粒爆开，每秒可能只有一两颗玉米粒爆开；在10～15秒之后，玉米粒就进入了疯狂“爆炸”的阶段，然后慢慢地，每秒爆开的玉米粒的数量又变少了，重新回到了一开始每秒只有一两颗玉米粒爆炸的状态。美国成年男性的身高分布也是对称的，要么比70英寸的平均身高略高，要么略低，而且越接近平均身高，人数越多。每一次SAT考试都经过精心设计，以得到一个平均分为500分、标准差为100的成绩的正态分布。根据《华尔街日报》的报道，美国人甚至连在购物商场停车都呈现出正态分布，正对着商场入口的地方停车数量最多，也就是正态曲线的“峰值”，在入口左右两侧的停车数量逐渐变少，即曲线两端下滑的“尾巴”。

正态分布的“美”好比迈克尔·乔丹在球场上的力量、灵巧和优雅，它来自于一个事实，那就是我们通过定义就能够清楚地知道，有多少数值位于平均值一个标准差的范围之内（68.2%），有多少数值位于两个标准差的范围以内（95.4%），还有多少数值位于3个标准差的范围以内（99.7%），以此类推。这听上去似乎挺傻的，但事实上这就是统计学的基础之一。本书将会在之后的篇章中谈到更深层次的问题时再对正态分布展开讨论。

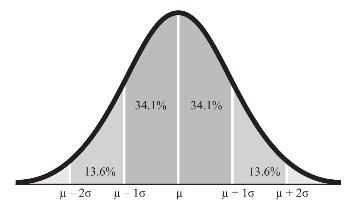
图2–3　正态分布

中间的那条线代表平均值，通常由希腊字母μ表示；标准差通常由希腊字母σ表示；每条色带均代表一个标准差。

描述统计学经常会比较两个数据或数量。例如，我比我的哥哥高1英寸，今天的气温比历史平均值高9摄氏度等。这些比较之所以易于理解，是因为我们大部分人都对其中所包含的数量单位并不陌生。当形容身高时，1英寸并不是很多，因此你可以推测我和我的哥哥的身高看上去其实差不多；相反的，无论是在一年中的哪个季节哪个时刻，9摄氏度都是一个非常引人注目的温差，因此我们可以说那一天比平时要热很多。但如果我告诉你，某品牌麦片中A配方的钠含量要比B配方高31毫克，除非你恰好懂得很多关于钠的知识（以及该品牌麦片的食用分量），否则上面这句话并不能给你带来特别具体的信息。又或者我对你说，我的外甥阿尔在2013年比2012年少挣了5.3万美元，我是不是应该对他表示担心呢？阿尔也许是一位对冲基金经理， 5.3万美元只不过是他年薪的一个零头。(www.xing528.com)

在钠含量和收入这两个例子里，我们都缺少背景资料。赋予这些比较型数据意义的最简单的方法就是使用百分比。如果我跟你说，某品牌麦片A配方的钠含量比B配方高了50%，我的外甥阿尔在2013年的收入与2012年相比减少了47%，是不是就更容易理解了？用百分比来表示变化，可以让我们有一种用刻度测量的感觉。

或许你在小学四年级的时候就已经学会如何计算百分比了，所以如果你想跳过接下来的几段文字，我表示理解，但在此之前，请帮我做一道简单的练习题。假设某家百货商场正在出售一款连衣裙，售价为每条100美元，随后该商场的副经理将所有商品的价格都下调了25%。但这位副经理很快就被解雇了，原因就是有人举报他在一家酒吧里跟比尔·盖茨喝酒。新来的副经理将所有商品的价格又上调了25%。那么那一款连衣裙最终的售价为多少？如果你说（或想说）100美元的话，那我建议你还是不要跳过接下来的任何一段话了。

连衣裙的最终售价应该是93.75美元。这不只是一个在鸡尾酒派对上用来逗乐和炫耀学问的把戏。百分数是一个非常有用的工具，但同时也容易产生混淆，甚至具有欺骗性。计算百分数差（或变化）的公式是这样的：（新数据–原数据）/ 原数据。分子（分数的上半部分）就是变化的绝对值，分母（分数的下半部分）的作用是将这一变化与原数据进行比较，也就是为变化添加背景。我们可以用这个简洁明了的公式解答刚刚提出的那个问题。前任副经理将每条价格为100美元的连衣裙的价格下调25%，那么原价100美元的25%就是25美元，这一折扣导致连衣裙的售价降为75美元。将这些数字带入公式也可以得到相同的结果：（100美元–75美元）/100美元=0.25=25%。

当连衣裙的价格为75美元时，新来的副经理将价格上调25%，这里就是许多人容易犯错的地方。上浮的25%参照的是连衣裙的新价格，而非最开始的价格，所以上涨的价格应该是25%×75美元= 18.75美元，最后的售价为75美元+18.75美元=93.75美元（而不是很多人认为的100美元）。这个例子的关键在于，百分数变动表示的是某个数字相对于其他事物的变化值，因此我们最好先弄清楚其他事物到底是什么。

我曾投资过大学室友开的一家公司。由于这是一家私营公司，因此在向股东披露信息方面并没有什么硬性要求。转眼几年过去了，我的这笔投资的命运如何，我毫不知情，我的这位前室友对于这个话题也是只字不提。最后，我终于收到了一封信，信上说公司的利润相比前一年提高了46%。但到底提高了多少美元，信上没写，也就是说我还是完全不知道自己的投资到底表现如何。假设上一年公司赢利27美分—基本等同于没有，那么这一年公司的赢利就为39美分—还是基本等同于零，但就从27美分到39美分来说，公司的利润的确上涨了46%，这一点没有问题。如果告诉你公司两年的累计赢利还不够买一杯星巴克咖啡，那么收到这样的股东信件可真够晦气的。

但是，我的室友是这样的人吗？显然不是。他最终把公司卖掉了，换回了数亿美元的资金，我的那份投资的回报率也高达100%。但你还是不知道我最后赚了多少钱，因为我并没有告诉你我最初投了多少钱，这不是更加能证明我的观点吗？读到这里，你是不是对什么是“其他事物”有点儿感觉了？

需要注意的是，百分差和百分率是不同的，我们千万不能混为一谈。比率通常会以百分数的形式体现，例如伊利诺伊州的消费税率为6.75%，我出书所得版税的15%要支付给我的代理商，诸如此类的比率都是基于某个定量来计算的，如所得税就是基于收入来征收的。可见百分率可以上浮，也可以下调，但百分差的描述方式就完全不同了，虽然两者的表述形式十分接近。最近就有一个绝佳的例子：伊利诺伊州的个人所得税税率由原来的3%上调到了5%。我们看到有两种不一样的说法来描述这一税率的变化，而且这两者在技术上都是正确的。主张并促成这次个税改革的民主党（正确无误地）指出，伊利诺伊州的个人所得税税率上升了两个百分点，从3%上涨到5%；共和党（同样正确无误地）指出，该州的所得税税率上升了67%，我们可以用刚刚学会的公式验证一下，（5－3）/3=2/3，即67%。

美国民主党将重点放在了税率的绝对变化上，而共和党则更关注税率的百分差。如刚才所说，两党在技术上都是正确的，但我可能会觉得共和党的描述更加准确地传达了税率变化所带来的影响，因为我以后要缴纳给政府的个人所得税—一笔我真的会在乎的钱—正如共和党所说的那样，确确实实上涨了67%。

许多现象都无法用一个数据来完美描述。就比如橄榄球比赛四分卫亚伦·罗杰斯的传球距离为365码，但没有触地得分；而另一个四分卫佩顿·曼宁的传球距离仅为127码，却完成了3次触地得分。曼宁创造了更多的得分，但按照常理，罗杰斯的长传球让他的队友得以突破对方球员的防守、在场上跑得更远。这两位四分卫谁的表现更好？在第1章中，我介绍了美国职业橄榄球联盟采用“传球效绩指数”来解决这一统计难题，它是一个描述性数据，而且是由许多其他描述性数据构成的。我们将这些从不同角度对比赛进行评价的数据浓缩成一个数字，并用这个数字进行比较，得出四分卫在某个比赛日中的排名，甚至整个职业生涯的四分卫排名等结论。如果棒球比赛也有一个类似的指数，那么本章一开始提出的历史上最伟大的棒球手是谁的问题是不是就有答案了？

将一系列复杂的信息浓缩成一个数字，这是所有指数都具备的优点。我们可以因此对原先无法展开简单比较的事物进行排名，从四分卫的表现到大学的优劣，再到选美比赛。在美国小姐选美比赛中，所有胜出者的成绩都是由5个部分的成绩组成的：个人面试、泳装展示、晚礼服展示、才艺表演和现场问答（“亲善小姐”称号的评选则单独由参赛者们相互评选产生）。

同时，将一系列复杂的信息浓缩成一个数字，这也是所有指数的缺点所在。我们有各种各样的方式来浓缩信息，每种方式都有可能导致一个不同的结果。马尔科姆·格雷德威尔在《纽约客》上发表了一篇批评性文章，用睿智的语言犀利地指出我们对排名的狂热（他尤其对大学排名嗤之以鼻）。格雷德威尔以《名车志》杂志对3款跑车的排名为例，这3款跑车分别是保时捷卡曼、雪佛兰科尔维特和莲花路特斯。《名车志》设计了一个计算公式，其中包含了21项评价指标，最终保时捷卡曼跑车拔得头筹。但格雷德威尔却指出，“外观”项在公式中的分量仅占到了4%，这一指标对于评价跑车来说简直低得离谱儿。如果将跑车外观的权重上调到25%，那么莲花路特斯跑车将会是第一名。

接下来，格雷德威尔还指出，跑车标价的分量在《名车志》的评价过程中相对来说也被低估了，如果上调标价比率（这样就能保证价格、外观和性能这三项指标在评价时各分秋色），那么雪佛兰科尔维特就将成为新的“跑车之王”。

所有指数均取决于其构成的描述性数据以及它们的权重，任何一点儿微小的变化都有可能引起结果的改变，因此，即使是最终得到的那个指数，可能是一种情况不完美但有现实意义的，也可能是完全不合理的。举一个前一种情况的例子—联合国的人类发展指数（HDI），这是一个比单纯的收入更加广泛的经济健康衡量指数。人类发展指数将收入作为评价的组成部分之一，同时还考虑到了寿命和受教育程度。美国在人均经济产出方面位居世界第11位（排在卡塔尔、文莱、科威特等几个石油国家之后），但在人类发展方面跃居全球第4名。的确，如果人类发展指数里的组成指标发生变化的话，最终的排名也会不一样，但可以肯定的是，只要是符合常理的调整，无论如何都不会出现津巴布韦超越挪威的结果。当我们想要了解全世界各地人民生活水平的差异时，人类发展指数为我们提供了一个简单方便且相对准确的排名。

描述统计学为我们所关心的现象打开了一扇窗，让我们更加接近事实的真相。好了，现在我们终于可以回到本章一开始提出的那些问题了。谁是史上最伟大的棒球运动员？结合本章所讲的主要内容，我们首先会问：哪些描述性数据最能帮助我们回答上述问题？根据棒球信息解决方案公司总裁史蒂夫·莫耶的说法，评价任何一个非投手运动员的3个最有价值的数据（除了年龄）是：

1.上垒率（OBP或OBA），就是球员上垒的概率，包括保送上垒在内（这一点是不包含在击球率的计算内的）。

2.长打率（SLG），就是衡量球员的长打得分能力的指标。一垒记1分，二垒记2分，三垒记3分，本垒记4分。也就是说，如果一个球员在5次打数中，打出了一个一垒和一个三垒，则其长打率为（1+3）/5=80%。

3.打数（AB），构成上垒率和长打率的比较背景。球技不佳的球员也会有发挥超常的时候，但仅限于某几场比赛。只有通过打数的积累，将成千上万次的击打表现综合起来，我们才能认定谁是真正的超级球员。

在莫耶看来，最伟大的棒球运动员非贝比·鲁斯莫属，因为贝比拥有无可比拟的击球和投球能力。直到今天，贝比·鲁斯创下的69%的长打率依然是大联盟球员难以撼动的生涯纪录。

那么，美国中产阶级的经济健康状况又是如何呢？我再一次将问题抛给了专家。我给杰夫·戈洛格（我在芝加哥大学的同事）和阿兰·克鲁格（研究恐怖分子的普林斯顿大学经济学家、美国总统奥巴马的高级经济顾问）发送了一封邮件，他们基本上给出了相同的答案，只有一些细节上的区别。要评价美国“中间阶级”的经济状况，我们需要了解（通货膨胀调整后的）工资中位数在过去几十年中的变化，他们还建议我留意一下处于第25百分位数和第75百分位数人群的工资变化，因为这两拨人通常被认为是中产阶级中的高收入和低收入人群。

还有一组必须分清楚的概念就是，在评价经济状况的过程中，不能将收入和工资等同起来。这两者是不同的，工资是我们付出的固定份额的劳动所得，如时薪或周薪；收入是全部所得的总和，来源有多种。如果一个工人找了一份兼职，或者加班很多个小时，那么这个人的收入会增多，但工资却没有发生变化。这就说明，即使一个人的工资下降，他的收入依然有可能上升，如果他加班足够多的话。但如果这些人不得不付出更多的劳动来取得更多的收入，那么我们很难评价他们的整体生活质量到底是更好还是更糟。因此，相比于收入来说，工资是评价美国人劳动收益的一个更加直观的指标，工资越高，工人们每工作1小时能领到的钱也就越多。

说了那么多，下面我们来看一幅过去30年美国人工资水平的变化图，在图中我还加入了第90百分位数人群的数据，以此对比相同时间内中产阶级工人和10%最富裕人群的工资增长水平。

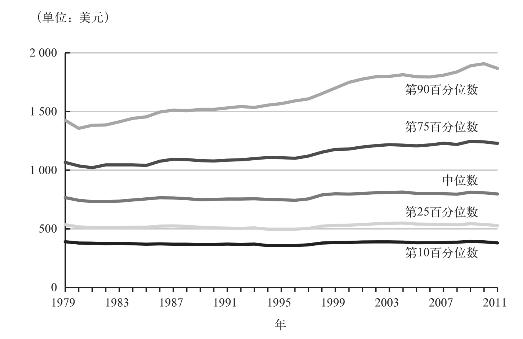
图2–4　不同收入群体的周薪变化

资料来源：《1979～2009年美国工人时薪分配变化》，美国国会预算办公室，2011年2月16日。图中具体数据参见http://www.cbo.gov/sites/default/files/cbofiles/ftpdocs/120xx/doc12051/02-16-wagedispersion.pdf

从这些数据中，我们可以得出有关中产阶级经济状况的各种结论，但都不会共同指向一个唯一“正确”的答案。从中我们能看到，典型的美国工人挣着中位数工资，在原地踏步了将近30年；但处于第90百分位数的富人们就好多了。幸好有描述统计学，我们终于在这个问题上构建出了一个框架，如果还要接着往下做点什么的话，那就是其他理论家和政治家的事情了。

本章补充知识点

表2–1　打印机质量问题统计表

方差和标准差的运算公式

方差和标准差是测量和描述数据分布的离散情况最常用的统计学技巧。方差通常用符号σ2表示，体现各个数值距离它们的平均值的距离远近。但要注意的是，在计算时需要对具体数值和平均值之差进行平方，然后再用平方数之和除以数值的个数。

举例说明：

假设有一组数量为n的数字x1、x2、x3 ……xn，它们的平均值为μ。

它们的方差σ2 = [（x1–μ）2 +（x2–μ）2+（x3–μ）2+……+（xn–μ）2 ] /n。

由于在计算方差时对每个数值和平均值之差都进行了平方，因此那些远离平均值的数值即异常值就会被放大，下面以学生身高为例。

表2–2　身高统计

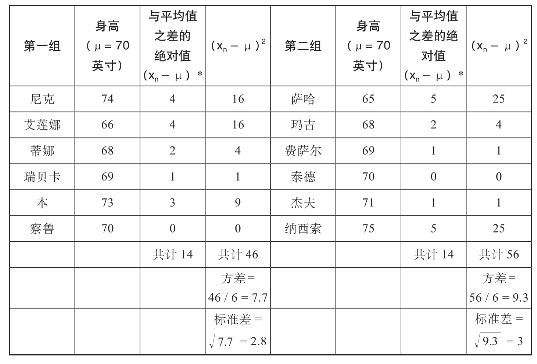
* 与平均值之差的绝对值表示两个数值之间的距离，不考虑方向（正负）因素，因此绝对值总是为正。这里的绝对值表示的是每个人的身高与平均身高之间相差的英寸数。

两组学生的平均身高都是70英寸，每一组学生个体与平均值的差异之和也都是14，到目前为止，这两组学生身高的离散程度是完全相同的。但是，第二组学生身高的方差要大些，这是因为萨哈和纳西索两个学生的身高数值距离平均值比其他学生都要远，从而导致了方差计算公式中的分子值变大。

在描述统计学中，方差很少被直接用于结论当中，往往是作为计算标准差的中间环节，而标准差才是一个更为直观的描述性数据。

标准差就是方差的平方根，计算公式如下：

假设有一组数量为n的数字x1、x2、x3 ……xn，它们的平均值为μ。

它们的标准差

【注释】

[1]吧台前一共有12个人，那么中位数应该是收入排在第六位和第七位的两个人的平均值，而这两个人的收入都是3.5万美元，因此中位数也是3.5万美元。如果一个人挣3.5万美元，另一个人挣3.6万美元，那么整组人的收入中位数则为3.55万美元。