全球零部件贸易的距离弹性差异

本书将全球范围内的40个样本国家按照收入水平进行分组，以检验不同收入组的距离弹性差异。表6.3—表6.6中，给出了回归方程1和回归方程2所得回归结果中各收入组的距离弹性值。

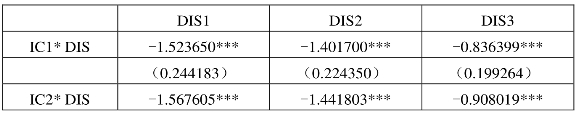
表6.3　距离弹性差异的基本引力模型回归结果——回归方程1（四组分组）

续表

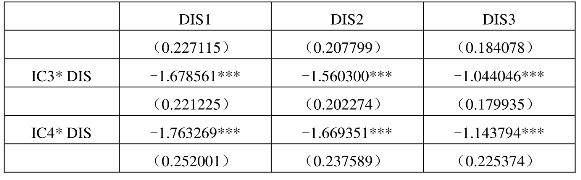
表6.4　距离弹性差异的扩展引力模型回归结果——回归方程2（四组分组）

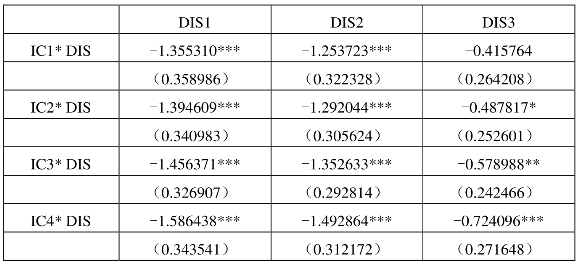
表6.5　距离弹性差异的基本引力模型回归结果——回归方程1（五组分组）(www.xing528.com)

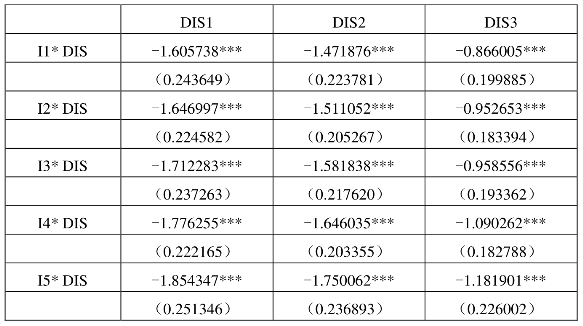
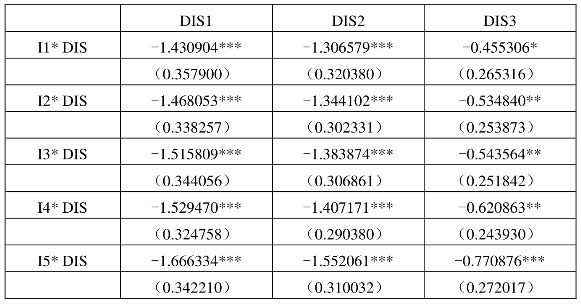
表6.6　距离弹性差异的扩展引力模型回归结果——回归方程2（五组分组）

（一）基本引力模型中的距离弹性差异

本书首先在基本引力模型基础上对零部件贸易的距离弹性差异进行检验。表6.3和表6.5中回归结果显示，距离变量DIS与表示收入分组的虚拟变量之间的交叉项系数值变化规律为：随着收入水平的下降（IC1-IC4，I1-I5），距离弹性值逐渐增大。这一结果表明，随着出口国收入水平降低，其零部件出口的距离弹性不断增加。

以上回归结果很好的验证了零部件贸易的“华盛顿苹果效应”，来自低收入等级的零部件（低技术等级零部件）对距离反映更为敏感。为保证回归结果的稳健性，文章仍然沿用第四节的方法分别用三个距离指标进行回归，估计结果都得到一致的结论。

（二）扩展引力模型中的距离弹性差异

本书在扩展引力模型基础上再次对零部件贸易的距离弹性差异进行检验。表6.4和表6.6中回归结果显示，各收入组之间的距离弹性差异仍然存在，并依旧表现为零部件贸易的距离弹性随出口国收入水平降低而不断增加。在此，本书也同样用三个距离指标进行回归，估计结果都得到一致的结论。其中，在以广州为贸易重心的距离变量DIS3回归结果中，不仅距离弹性系数值随收入水平下降而增加，而且距离变量的显著性也随着收入水平的下降而有所增强。