数据集分类评价方法：定性与定量分析比较

目前对数据集进行分类评价的方法主要有两类：基于经验的定性分析和基于客观数据的定量分析。较为常见的定性分析方法包括层次分析法和模糊评价法。此类方法主要依靠经验对各级评价指标赋予一定权重，通过研究者对其权重的分析匹配后对数据进行处理。这类方法因具有主观性，对研究者的经验水平要求较高，如果出现主观评判方面的失误，可能会使研究结果产生较大偏离。另一类方法为定量分析，这类方法各层指标的权重由样本数据决定，但对数据样本选择的准确性要求较高。常用的方法有灰度关联分析法和主成分分析法。用定量与定性相结合的方法对问题进行研究则是比较理想的状态，但是鉴于作者在经验等方面受限，本研究选择使用主成分分析法来研究问题。

主成分分析法是将多指标化为少数几个综合指标的一种统计方法。其具体做法为通过多个指标的线性规划，将众多错综复杂的一系列指标归结为少数几个综合指标（即主成分），使各主成分既保持相互独立，又没有信息重叠，从而更集中更典型地表明研究对象的主要矛盾。

（1）主成分分析法的数学原理

主成分分析法的原理是：线性变换实质上是一种坐标变换，利用线性变换的思想，可以通过坐标变换从原有特征中得到一批数量相同的新特征，新特征集合包含了原有各特征的信息，且这些新特征中的某几个可能包含了原有特征中的主要信息。因此，保留几个包含主要信息的特征作为近似系统识别的新特征，可达到减少特征数量的目的，实现系统识别特征简化，这就是主成分分析法的思想。具体来讲，主成分分析法就是设法将原来众多的具有一定相关性的指标（比如p个指标），重新组合成一组新的相互无关的综合指标来代替原来的指标，通常在数学上的处理就是将原来p个指标作线性组合。在主成分分析法中，将选取的第一个线性组合即第一个综合指标记为F 1，自然希望F 1尽可能多地涵盖原来指标的信息，表达“信息”最经典的方法就是用F 1的方差来表达，即Var（F 1）越大，表示F 1包含的信息越多。故所有线性组合中方差最大的F 1应作为第一主成分。如果第一主成分不足以代表原来p个指标的信息，再考虑选取F 2即选第二个线性组合。为了有效地反映原来信息，F 1已有的信息就不再需要出现在F 2中，用数学语言表达就是要求Cov（F 1，F 2）=0，称F 2为第二主成分，依次类推可以造出第三、第四……第p个主成分，不难想象这些主成分之间不仅不相关，而且它们的方差依次递减。因此在实际工作中，就挑选前几个最大主成分，虽然这样做会损失一部分信息（原则上选取λ＞1的特征根对应的主成分），但是由于抓住了主要矛盾，并从原始数据中进一步提取了某些新的信息，这种既减少了变量的数量又抓住了主要矛盾的做法有利于问题的分析和解决。

若把样本取得的原始数据看作变量X1，X2，X3，…，Xn，为消除这些指标中相互重叠的信息，形成新的综合指标Z1，Z2，Z3，…，Zm，（m≤n），形成新的方程：

在确定系数lij时，首先要保证Zi与Zj（i≠j；i，j=1，2，3，…，m）相互不关联，其次是Z1代表X1到Xn中线性组合方差最大者；Z2代表与Z1不相关的X1到Xn中线性组合方差最大者，一般理解为线性组合中方差第二大者；……Zm代表与Z1、Z2，…，Zm-1均不相关的X1到Xn中线性组合方差最大者。至此，Z1，Z2，Z3，…，Zm组成了原变量X1，X2，X3，…，Xn的第一、第二乃至第m主成分，而在实际问题讨论中，一般选择对样本贡献率较大的主成分作为参考。(www.xing528.com)

（2）主成分分析法的计算过程

计算特征值。通常情况下会选用雅克比法则对|λI-R|=0此类特征方程求解，求出的特征值λi（i=1，2，…，n），并按照大小排序：λ1≥λ2≥λ3≥…≥λp≥0。然后求解特征值λi的特征向量ei（i=1，2，3，…，n），要求||ei||=0，既此处eij代表了ei的第j个分量。最后检验矩阵的一致性：①计算一致性指标其中λmax为判断矩阵的最大特征根，n为矩阵的阶数。②判断矩阵的平均随机一致性指标RI值，对于2，3，4，5，6，7，8，9阶矩阵，RI值分别为0.00，0.58，0.90，1.12，1.24，1.32，1.41，1.45。③当随机一致性比率CI/RI＜0.1时，则认为判断矩阵一致性良好；否则，认为判断矩阵一致性差，需要重新标度判断矩阵，直到达到良好的一致性为止。

计算主成分贡献率及累计贡献率。第zi个主成分的贡献率计算方法为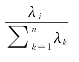（i=1，2，3，…，n）。累计贡献率计算方法为

主成分分析法要选取尽量少的k个主成分（k＜p）来进行综合评价，同时还要使损失的信息量尽可能少。k值由累计贡献率来决定。在定量分析中，贡献率是衡量各因子相对重要程度的指标。称为第一主成分贡献率，这个值越大，表明第一主成分综合X1，X2，…，Xp信息的能力越强。前k个主成分的累计贡献率为，即前k个主成分的贡献率达到65%，表明取前k个主成分基本包含了全部测量指标的信息。方差贡献率的大小，表示各个主成分的相对重要程度。本研究按照特征值大于1以及累计贡献率大于65%的原则提取主成分因子，将标准化后的指标变量转换为主成分：F（X）=ω1x1+ω2x2+…+ωnxn。F1称为第一主成分，……F2称为第二主成分，……Fn称为第n主成分。先求每一个主成分的线性加权值，Fn=ω1x1+ω2x2+…+ωnxn，再对n个主成分进行加权求和，继而获得决策评价排序。权数为每个主成分的方差贡献率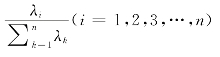，最终评价值