市场调查中的抽样技术优化方案

汽车市场调查还涉及调查对象的选择问题。调查对象的选择方法又可分为：全面普查、重点调查、典型调查和抽样调查4 种，其中抽样调查是市场调查中被广泛使用的一种方法。

一、抽样调查的基本概念

（一）信息源及其特征

信息源，就是有关事件的记录或信息内容发生和存在的地方，也就是人们所要收集资料的地方或对象。进行市场调查首先必须回答从何处收集资料的问题，因此只有找对信息源才有可能收集充分的、有用的资料或信息。

正确识别信息源，是进行市场调查的关键步骤。一般来说，信息源应具有这样以下几个特征：

（1）与有关事件或信息内容的联系最密切。

（2）对有关事件发生过程或信息内容有完整的记录或记忆。

（3）具有对有关事件发生过程或信息内容的长期记忆功能或记录保持功能。

（4）在一定的条件下能够讲述或再现有关事件的全貌。

例如，若要收集某品牌汽车商品在市场上最近几个月的销售数量及其增长的情报资料，下面几个地方哪一个是真正的信息源？

A.政府的统计机关

B.政府的工商管理机关

C.消费者

D.汽车商店

显然，汽车商店是销售有关商品的地方。汽车商店和消费者都是有关事件（最近几个月汽车商品的销售）的主要行为人，因而与该事件具有密切的联系。政府的统计机关和工商管理机关通常不会关心或介入有关商品的销售。而一个消费者只会记忆或记录自己的消费购买，不会对市场上某种汽车商品几个月来的销售量做记录，该记录只有商店才有。商店的销售记录或相应账目通常会保存较长时间，在调查中能够获得全面、完整地说明有关商品的实际销售量及其增长情况的信息。所以，对于这个问题，汽车商店才是真正的信息源。

（二）总体、样本和抽样调查

信息源全体成员称为总体（也称母体），而被抽取出来作为调查对象的成员称为样本。为了节约费用，快速完成调研任务，必须在全部对象（即总体）中选择具有代表性的一部分（样本）加以调查，然后以样本的统计特征值推断总体特征值。这种调查称为抽样调查，其原理如图2.8 所示。

图2.8　总体与样本的关系

特征就是指总体和样本的某个属性，如性别、年龄、职业等。一组互斥的属性特征集合为变量。总体中某一变量的综合描述称为总体特征值（简称总体值），它反映总体中所有元素的某种特征的综合数量表现。调查样本中某一变量的综合描述称为统计特征值（简称统计值），它反映样本中所有元素的某种特征的综合数量表现。我们往往用平均值与标准差来反映某一特征值，并用统计值作为总体值的估计值。这就是抽样调查的原理。

（三）抽样和抽样框

抽样，即从总体中抽出一部分样本。样本应当具有代表性，本身具有（因而能反映）总体的特征。例如，在对消费者进行抽样调查时，所选择被调查的消费者应当与其他消费者具有相似的收入水平、消费习惯、文化背景、消费层次和市场环境。如果不同，所调查的消费者信息就不能反映其他消费者的信息，在从样本特征值推断总体特征值时，就会发生偏差。在消费者之间存在差异的情况下，必须选择特征不同的消费者，避免以偏概全。

抽样框又称抽样范围，是指一次直接抽样时总体中所有抽样单位的名单。样本或某些阶段的样本从抽样框中选取。

例如，从一个社区的全体家庭中，直接抽取200 个家庭作为样本。那么，这个社区全体家庭的名单就是这次抽样的抽样框。如果是从这个社区的所有单元中抽取部分单元的家庭作为调查的样本，那么，此时的抽样框就不再是全社区家庭的名单，而是全社区所有单元的名单。因为此时的抽样单位已不再是家庭，而是单元。

二、抽样调查的基本程序

抽样调查的基本程序如图2.9 所示。

图2.9　抽样调查的基本程序

下面就样本大小的确定和抽样方法两个问题做出讨论。

三、样本数量的确定

样本数量可以影响调查数据的质量，它在很大程度上取决于个体之间的相似程度和相关信息的种类。如果总体中个体之间高度相似，任意选取一个样本就可以比较清楚地说明总体的特征。但是，如果个体之间存在较大差异，且要求样本统计特征值能够反映和说明总体的情况，就需要选取较多的个体作为样本。

样本数量的确定方法有多种，这里主要介绍一种常用的、较为准确的数量方法——置信区间法。要理解这种方法，首先要确定可信度。

可信度是表明特定样本的估计值被视为对总体参数的真实估计的准确与可靠程度的概念。与可信度对应的是误差的显著性水平。95%的置信水平（表示样本估计值落入可信区间的概率为0.95）对应有5%的误差显著性水平，而99%的置信水平对应有1%的误差显著性水平。这两种显著性水平是经常采用的。有关可信区间等统计学概念，请参阅统计学教材。

对每个样本进行调查取得的某种数据称为样本值。抽样调查取得的该类数据的全部样本值可被用于计算样本平均值以及标准方差。样本平均值反映全部样本的某种数据的平均水平，通常记为；标准方差则反映各个样本值在平均值周围分散的程度或离散度，记为S。有些情况下也用到样本平均值的标准误差（SEx）。如果这个统计数据大，那么该样本估计值与总体参数的真实值偏差也大；如果这个数据较小，就可以相信样本估计值是一个较好的、可靠的总体参数的代表。

不论样本数量多大，在将样本平均值视为总体均值时，总是存在一定的误差。统计学理论证明，样本平均值的标准误差大小与样本数量的平方根呈反比。这一定理用数学公式来表达就是：

式中　σ——总体的标准方差；

　　　n——样本数量。

根据上述定理，不难推导：

这就是用来计算样本数量的数学公式。可运用该公式计算已知总体的标准方差。另外，必须知道可接受的标准误差值。一般情况下，总体的标准方差是不知道的，因而要以K 个个体组成的样本组的标准方差来代替。K 个个体构成的样本组的标准方差可作为总体方差的一个合理估计，用下式计算：

另一个可用于计算简单随机抽样的样本数量的数学公式是：

式中　——Z 的统计量，对应于希望达到的置信水平。在正态分布下，95%的置信水平所对应的为1.96；99%的置信水平所对应的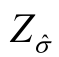为2.58。

　　　E——可接受的最大误差（即精确度为±E%）。

计算示例：

以95%的可信度对一支销售队伍的平均销售能力进行随机抽样调查，如果要求样本平均值与总体真实平均值之间可接受的最大误差量为2.0。假定=12 时，样本数量为多大？

因为对应于95%的置信水平，Z=1.96。所以

由公式也可以发现，要提高样本估计值的准确度，虽然可以通过增加样本数量来实现，但是，需增加的样本数量将呈二次指数速度增长。具体而言，一个样本数量是1 000的抽样调查结果所存在的样本误差只是一个样本数量为4 000 的样本误差的2 倍。或者说，一个样本数量是4 000 的样本误差只是样本数量为1 000 的样本误差的l/2，因为样本误差之比为

调查费用也是影响样本数量的决定因素之一。调查活动的费用总是随着样本的增多而增加的，选择的样本数量越大，所需投入的资金、人力、物力就越多。从节约费用的角度考虑，样本数量应当小一些。

四、抽样方法

调查样本的选取对抽样调查结果有极为重要的影响。按抽样原则不同可以将抽样方法进行分类，如图2.10 所示。(www.xing528.com)

图2.10　抽样方法分类

（一）随机抽样

随机抽样是按照随机原则从总体单位中抽取样本的抽样方法。这种抽样方法具有统计推算的功能，能如实地算出样本的代表性程度，还可以判断抽样误差。但这种抽样方法不省钱、不省时、不方便。

（1）单纯随机抽样。即总体中每个成员被选中的机会相等的一种随机抽样方法。采用单纯随机抽样，可用统计学方法来排除选择过程中的人为偏差。

① 抽签法。常用一个骰子，这个骰子必须使0～9 的数字都能得到同等的出现机会，一个立体正十方形的骰子，可以满足需要。

例如，要从1 000 个样本中选出10 个样本，则将这个骰子转动3 次，以最先得到的数字为百位，第2 次为十位，第3 次为个位，组成一个数，反复转动骰子，可得到一组数据，即为样本的序号。

② 利用乱数表法。乱数表是用骰子投掷得出来的数字列出的一张表。

例如，以下是乱数表的一部分，供作参考。

乱数表（部分）：

（2）分层随机抽样。它是指先将总体单位按其属性特征分成若干层次，层与层之间差别较大，层内各单位情况类似，然后再从各层内随机抽取样本的抽样方法。

分层抽样的关键在于层的划分。分层时要注意如下问题：

① 层与层之间的界限，每一个单位都归属于一定的层，不允许交叉或者有所遗漏；

② 要知道各层中的单位数目及占总体的比重；

③ 分层不宜过多，否则不便于从每层中抽样。

常见分层方法如下：

① 按性别或职业分层；

② 按零售店规模大小分层；

③ 按消费者所得分层；

④ 按年龄分层。

（3）分群随机抽样。它是将总体各单位按一定标准分成若干群体，然后按照随机原则从这些群体中抽选部分群体作为样本，对作为样本的群体中的每个单位逐个进行调查。这种抽样方法适用于个体界限不清的总体。因为总体的差异性很小，而且比较乱，便不能订立标准分层，只能依其他外观的或地域的标准来划分成几个群。

例如，拟从某市抽出1 000 个样本，但无法取得该市市民名册，所有资料只有小区、办事处的名称和数目。假定该市共有200 个单位的小区、办事处，每一个单位约有20 名居民，因此可以以小区、办事处为单位，从200 个小区、办事处中随机抽出 50 个，并将所抽出的小区、办事处中的全体居民作为样本，如此可抽出1 000 个样本。

分群抽样与分层抽样在形式上有相似之处，但实际上差别很大。分层抽样要求各层之间的差异大，层内个体或单元差异小，而分群抽样要求群与群之间的差异比较小，群内个体或单元差异大；分层抽样的样本是从每个层内抽取若干单元或个体，而分群抽样则是要么整群抽取，要么整群不被抽取。

（二）系统抽样

系统抽样又称等距抽样。它是将总体中各个体按某一特征（或编号）排列，然后依固定的顺序和间隔抽取样本。系统抽样介于随机抽样和非随机抽样之间。抽样流程如下：

抽样前，须将总体的每一个单位编号，先计算样本区间（即N/n，N 表示总体的数目，n表示样本的大小），如果样本区间为分数，可四舍五入化为整数。然后从l 到N/n 号中随机抽出一个号码作为第一个样本单位，将第一个样本单位的号码加上样本区间即得第二个样本单位，依此类推，直到样本数足够为止。

其第一个样本单位可以依判断抽样（内容见后）抽取，亦可用随机方式抽取。

例如，总体样本有10 000 个，样本的大小为200 个，则样本区间为10 000/200—50，假如从1 到50 中我们随机抽出了7，则样本单位的号码，依次为7，57，107，157，207，…，直到样本达到200 个为止。

它适用于对零售店数据的常规调查。

（三）非随机抽样

非随机抽样不是遵循随机原则，而是调查人员根据自己的主观选择抽取样本的方法。这种抽样方法主要应用于抽样总体太庞大、太复杂时，无法判断误差并无法估计抽样误差。与随机抽样相比，这种抽样方法省钱、省时、方便。

（1）任意抽样。任意抽样又称随意抽样，是随调查者之方便而选取样本。总体的标志是“同质”时，可用此法。

常见的做法是街头访问调查（看到谁就访问谁）。

其优点：使用方便，最省钱。

其缺点：抽样偏差极大，结果极不可靠，因此通常不应利用一个任意抽样样本估计总体变量的数值，因为一个总体中“任意”单位极可能和其他“不任意”的单位有显著的不同。

（2）判断抽样。判断抽样又称立意抽样，是由专家的判断来决定所选的样本。

使用这种方法时必须对总体的有关特征非常相当了解。

使用这种抽样法应极力避免挑选极端的类型，而选取“多数型”或“平均型”的样本为调查研究的对象，以期通过对典型样本的研究来了解总体的状态。

在编制物价指数时，有关产品项目的选择及样本地区的确定等常采用此法。

其优点：由于判断抽样法是依照调查人的需要选定样本，故较能适合特殊的需要，回收率也较高。

其缺点：如果主观判断偏差，则判断抽样极易发生抽样误差，故它适用于总体的构成单位极不相同而样本数很小的情况。

（3）配额抽样。它是按照一定的标准（即分层标准）和比例分配样本数额，然后由调查人员在分配的额度内任意抽取样本的一种方法。它适用于小的市场调查。

执行步骤如下：

① 选择“控制特征”作为细分总体的标准；

② 将总体按“控制特征”细分，将其分成数个子总体；

③ 确定各子总体样本的大小，通常是将总样本数按各子总体在总体中所占的比例分配。

采用此法时，为了明了样本在各层中的分配状况，必须先拟出一个样本交叉控制表。

例如，为了调查某品牌汽车不同客户的满意度，需抽取样本总数20人，其中，男、女各为9、11人，社会阶层上、中、下等各为2、4、14 个，年龄20～29，30～44，45～64，65以上分别为4、6、7、3人，则该样本的交叉控制表如表2.19 所示。

表2.19　交叉控制表

表2.19 中的社会阶层、性别、年龄就是控制特征，这些控制特征交叉部分就形成了一个子总体。

④ 选择样本单位：各子总体样本数确定后，即可采用任意抽样法为每一个调查员指派“配额”，要他在某个子总体中访问一定数额的样本。