破头乘法：提高运算效率的乘法方法

(一)破头乘法

在珠算中，破头乘法是指当被乘数与乘数的首位数相乘时，由于被乘数的本位要改拨乘积的十位数而被破掉，因此这种乘法叫破头乘法。其运算步骤与方法如下。

1. 置数和定位

破头乘法与空盘前乘法不同，首先要拨置被乘数，被乘数拨置的位置由采用的定位方法而定。用公式定位法，应首先选一个定位点——被乘数首位非0 数字的置数档次，然后依次拨入其他数字，运算结束后，如果积的首位落在该定位点上，则采用公式(3-1)确定乘积的位数；如果积的首位落在定位点的右一档上，则采用公式(3-2)确定乘积的位数。

2. 运算顺序

在破头乘法中，当被乘数各位与乘数的某位相乘时，其顺序与空盘前乘法的运算顺序正好相反。

首先用被乘数的末位数(非0 数)与乘数的首位(非0 数)相乘，乘积为首积。再用被乘数的末位数与乘数的第2 位、第3 位……从右至左依次相乘，直到乘数的末位同被乘数的末位乘完为止。最后用被乘数的第2 位数采用同样的运算顺序从右至左依次乘算，直至被乘数的最高位同乘数的末位乘完为止，如图3-58 所示。

图3-58

3. 加积档位

①被乘数的末位与乘数的最高位的乘积为首积，首积的十位由被乘数末位改拨而成，其右一档拨入首积的个位数，此次乘积的个位档为下次乘积的十位所拨加的档次，其右一档为下次乘积的个位拨加的档次，依次递位迭加。

②乘积的顺序为：首先由被乘数的末位与乘数的各位(从高位到低位)相乘，递位迭加拨珠入盘；然后，由被乘数的末2 位、末3 位……分别与乘数的各位相乘，将乘积拨入正确的档次。运算如图3-59 所示。

图3-59

在运算中，为了避免出现将乘积加错档次的问题，可以运用以下规律进行拨加，即：先牢记被乘数，被乘数的哪一位与乘数的最高位相乘，就在被乘数那一档上拨入积的十位数，右一档拨入积的个位数，然后递位迭加被乘数这一位与乘数各位依次乘积的结果。

例3-32　0.84×2.6=2.18(保留两位小数)

(1)采用公式定位法，确定一个定位点档，从此档依次拨入被乘数(从非0 数字开始)，并默记乘数，如图3-60 所示。

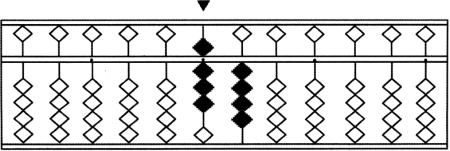
图3-60

(2)用被乘数的末位数4 同乘数的最高位2 相乘，“四二08”，将被乘数本位数字4 改成积的十位数0，在右一档加上积的个位数8，将手指停留在该档上，如图3-61 所示。

图3-61

(3)用被乘数的末位数4 同乘数的第2 位数6 相乘，“四六24”，将积的十位数2加在手指停留的档上，右一档拨加积的个位数4，如图3-62 所示。

图3-62

(4)用被乘数的末2 位数8 同乘数的最高位相乘，“八二16”，将被乘数8 改成积的十位数1，在下一档加上积的个位数6，将手指停留在该档上，如图3-63 所示。

图3-63

5)用被乘数的末2 位数8 同乘数的第二位数6 相乘，“八六48”，将积的十位数4加在手指停留的档上，右一档拨加积的个位数8，如图3-64 所示。

图3-64

采用公式定位法，定位点上有数字2，运用公式(3-1)，M+N=0+1 位=+1 位，积为2.184。

采用破头乘法运算时，被乘数从末位至首位分别与乘数各位按读数顺序自左向右相乘，同其他乘法相比较，减少了隔位跳位，因此速度快。但是破头乘法在拨加首积时，被乘数即被破掉，以后再与乘数其他位相乘时，必须用脑将原被乘数记住，不能再直观乘算，因此掌握破头乘法的难度比较大，需要熟记、熟用“大九九口诀”，做到脑手合一，才能很好地运用。

(二)省乘法

省乘法也称省略乘法、截尾乘法。它是根据计算结果要求的合理精确度，用四舍五入法删掉乘数与被乘数中某些位数上的数字，运用近似计算的方法，省略一些计算过程，并对积数的尾数加以适当处理，从而提高运算效率的一种方法。

其运算方法和步骤如下。

(1)先用截取公式求所需计算的位数码。

截取公式=m+n+精确度+保险系数1 位(运用截取公式一般结合固定个位法进行)

(2)在盘上固定个位档。(www.xing528.com)

(3)被乘数按m+n 定出的位数，按固定个位档定位法拨入盘中。在个位后面留出小数点数码，再加1 位保险系数。截留位码后，其末位定为压尾档(又称截止档，用“▽”表示)。

(4)用基本乘法运算，计算时一律算到压尾档为止，以下四舍五入。

例3-33　3.871 267×7.836 23=30.34(精确到0.01)

(1)先用截取公式求出位数码：m+n+精确度+保险系数1 位=5 位。按固定个位法拨被乘数入盘，记住小数点保留两位，再加保险系数1 位，末位看作压尾档。计算时算到压尾档为止，如图3-65 所示。

图3-65

(2)被乘数末位3 乘以乘数首位7，“三七21”，压尾档下一位1 舍去，乘数7 以下可不再乘了。盘面数为38 712，如图3-66 所示。

图3-66

(3)被乘数的倒数第2 位1 乘以乘数78 即可。“一七07”，“一八08”，压尾档下一位数8 进上来。盘面数为38 710，如图3-67 所示。

图3-67

(4)被乘数倒数第3 位7 乘以乘数783 即可。“七七49”，“七八56”，“七三21”，压尾档下一位数1 舍去。盘面数为38 558，如图3-68 所示。

图3-68

(5)被乘数倒数第4 位8 乘以乘数7 836 即可。“八七56”，“八八64”，“八三24”，“八六48”，压尾档下一位8，四舍五入。盘面数为36 827，如图3-69 所示。

图3-69

(6)被乘数首位数3 乘以乘数78 362 即可。得积数30 336，如图3-70 所示。

图3-70

(7)最后得数为30.34。

例3-34　64.97×6.893=447.84

省乘法也可以用空盘前乘法来进行运算。

(1)用固定个位法确定小数点，方法同上。

(2)确定被乘数与乘数首位乘积的十位的入盘档次。用“大九九”口诀乘法，被乘数与乘数首位乘积的十位数入盘档次=被乘数的位数+乘数的位数=m+n，本题中为2+1=3。

(3)用空盘前乘法运算拨入算盘，运算截止档到下一位，该位做四舍五入处理。乘数首位6 乘被乘数6 497，从算盘+3 档位起加积，盘面数为38 892，如图3-71 所示。

图3-71

(4)乘数次位8 乘6 497，从算盘+2 档位起加积，盘面数为441 796，如图3-72 所示。

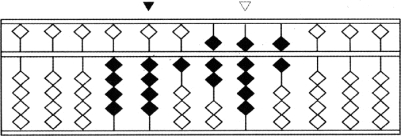
图3-72

(5)乘数第3 位9 乘6 497，从算盘+1 档位起加积，将“九七63”的3 舍去，盘面数为447 643，如图3-73 所示。

图3-73

(6)乘数第4 位3 乘6 497，从算盘的0 档位开始加积，“三六18”，“三四12”，“三九27”，将7 进上来，后面就不用再乘了，盘面数为447 838，如图3-74 所示。

图3-74

(7)截止档上的数四舍五入后，得积447.84。