动态能力指标体系应用评价流程解析

通过上节信度效度分析可以得出，这份问卷是合理具有可操作性的。本节主要进行以下两项工作：一是进行因子分析，从指标体系中提取不同的公因子；二是按照神经网络的要求随机选取样本进行应用评价分析。

1.动态能力指标体系的因子分析

因子分析过程主要分为四步：第一步，根据KMO值判断是否适合进行因子分析。KMO值越大，说明指标之间的相关性越大，越适合进行因子分析。一般规定KMO低于0.5，Bartlett球形检验显著性p大于0.05时，是不适宜进行因子分析的。第二步，因子的提取。通过分析众多指标的相互关系，提取出数量较少的因子，通常是基于主成分分析法提取特征值大于1的因子。第三步，因子旋转。利用因子分析法提取的因子之间虽然有正交性，即彼此之间不相关，但是往往对原始指标的解释能力较弱，难以解释并命名，所以对因子进行旋转，将易于对提取的公因子进行命名和解释。本研究采用方差最大正交旋转法。第四步，计算因子得分。利用因子表示原始的众多指标，需要知道因子与这些指标之间的线性关系。也为因子命名提供依据，本研究采用系统默认的回归法计算因子得分。

由表3-11所示，四个维度的KMO值均大于0.5，适合做因子分析。

（1）环境感知维度指标的因子分析

环境感知维度共有5个指标，据此设计出了包含5个题项的量表。量表因子分析结果如表3-12所示。因子分析后各个指标在提取的某个因子上的载荷均高于0.7，两个特征值分别为2.235和1.588，因子累积方差贡献率为76.464％，大于60％。

因子1包含了S3、S7、S6三个指标，主要反映旅游社会企业感知外部利益相关者变化的反应，因此将其命名为外部感知；因子2由S4、S5组成，主要反映的是旅游社会企业对内部氛围和匹配度的感知，所以将其命名为内部感知。

表3-12　环境感知维度指标的因子分析结果

（续表）

（2）整合协调维度指标的因子分析

整合协调维度一共有8个指标，根据此设计出了包含8个题项在内的量表。量表因子分析的结果如表3-13所示。因子分析后各个指标在提取的某个因子上的载荷均高于0.7，两个特征值分别为3.020和2.642，因子累积方差贡献率为70.767％。

因子1包含了C5、C8、C4、C6四个指标，反映了旅游社会企业如何整合内部关系和资源快速适应的过程，因此将其命名为内部流程效率。因子2包含了C2、C1、C7、C3四个指标，主要反映了旅游社会企业对外部利益相关者关系的维护和利用，将其名为关系网络的维持。

表3-13　整合协调维度指标的因子分析结果

（3）学习维度指标的因子分析

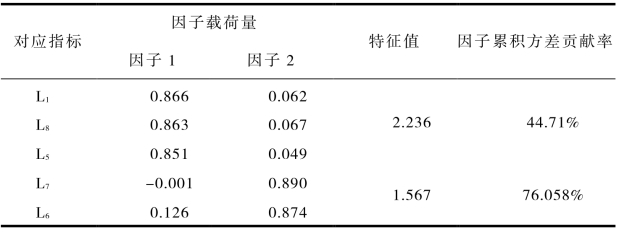
学习维度一共包含5个指标，根据此设计出了包括5个题项的量表。量表因子分析的结果见表3-14所示。因子分析后各个指标在提取的某个因子上的载荷同样满足均高于0.8，两个特征值分别为2.236、1.567，因子累积方差贡献率达到76.058％。

学习维度提取出了两个因子，因子1包括了L1、L8、L5三个指标，它们反映了旅游社会企业利用各种学习方式和渠道来填补企业知识信息缺口的过程，也是知识吸收、改变组织能力的过程，将其命名为学习机制。因子2包含L7、L6两个指标，这两个指标都是从旅游社会企业价值观和文化的角度来衡量学习的内容和效果，区别于一般企业的文化建设，将此因子命名为社会创业精神的培育。

表3-14　学习维度指标的因子分析结果

（4）整合与重构维度指标的因子分析

整合与重构维度包含7个指标，根据这7个指标设计出了包括7个题项的量表。量表因子分析的结果如表3-15所示。因子分析后各个指标在提取的某个因子上的载荷不低于0.8，三个特征值分别为2.352、1.734和1.600，因子累积方差贡献率为81.228％。

整合与重构维度一共提取了三个因子，因子1包括T3、T1和T7三个指标，主要从经营思路和流程上进行创新和调整，更新对于市场的定位，因此，因子1命名为创新能力。因子2包含了T4、T9两个指标，它们主要反映了企业在面临外部挑战时，为应对危机，内部组织作出的调整和增强风险应对的能力，因此将因子2命名为风险应对。因子3包含了T2和T10两个指标，反映了企业对于外部网络的扩展和整合以及扩展所引进的新技术和服务，因此命名为网络拓展因子。

表3-15　整合与重构维度指标的因子分析结果

由以上可知，因子分析的结果表明各个指标在某个因子上的因子负荷量均大于0.7，因此都选取进来，此外，在每个维度上，所有累积解释变异量都不低于70％，结果都比Zaltman和Burger认为的因子负荷量（大于0.3）和累积解释变异量（大于40％）的临界值要好。所以本节可以运用上文因子分析的结果。

2.BP神经网络设计过程

对于BP神经网络的创建将利用MatlabR2010b进行编程，实现网络的学习和训练功能。

（1）BP神经网络的设计

1）样本的准备。对于输入输出的表示，本节的输入量选择前文因子分析中确定的9个因子，输出量则是动态能力的数值。

由于不同意义的数据范围相差比较大，网络会区别识别，所以在建立BP神经网络前，要先将原始数据进行归一化处理对变量进行尺度的变换以便得到无量纲化的数据。利用Matlab的mapmin max函数进行数据的归一化，调用函数的格式表示为：［normInput，ps］=mapmin max（p）。

样本数量的确定对于整个网络质量的好坏也是很关键的，样本数量过多会影响到网络的精度，一般来说样本数量是连接权数的2～10倍，或者样本个数大于评价指标个数，占总样本数量的10％以上即可。本节为了正确评价网络的性能和泛化能力，从收集到的企业中随机抽取15家作为训练样本。

BP神经网络的算法要求通过期望值和训练的输出值不断比较和反复训练才能满足误差，动态能力没有一个现成的值可以作为期望值，现有的研究对于期望值的计算可以通过专家咨询、加权求和、模糊评价等得出。本书利用突变级数法计算评价指标体系中因子的值，最终得出动态能力的期望值。

突变级数法是将评价目标分解为各个层次，通过与模糊数学相结合的方法产生突变函数，由归一化公式进行运算，最终得出总的评价参数的一种综合评价方法。这个方法最大的特点是不考虑指标的权重，只参考同一层次中指标的相对重要性，本节中对于同一层次指标的相对重要性通过因子分析可以得出，且本节中利用因子分析对指标进行简化和浓缩，也使指标个数能够符合突变级数的要求，从而增加了整个过程的科学性和简洁性。突变级数法的常见的形式有尖点突变、燕尾突变和蝴蝶突变，各自的势函数分别为：f（x）=x4+ax2+bx；；，其中，a、b、c、d代表控制变量，2、3、4个指标分别对应着三个突变系统。

根据以上导出尖点突变、燕尾突变和蝴蝶突变的归一公式：。根据计算出的对应的X值运用大中取小的原则得出总评价指标的得分。

2）BP神经网络的结构设计

网络层数的确定，有研究表明，一个三层的网络可以映像所有的连续函数，隐含层数的增多会使网络复杂化，因此本节采用单隐含层的网络结构，即包含1个输入层、1个隐含层和1个输出层共三层的网络。

输入层节点数的确定，根据以上因子分析构建的评价指标体系以及各个指标的分析，输入层的节点数就是因子的数量，也就是9个。而输出层的节点数由评价目标所决定，本节研究的是旅游社会企业动态能力，要得到反映动态能力高低的一个数值，所以输出层的节点数即为1。

隐含层的节点数可以从样本中提取并保留内在规律，无数的节点可以实现任意精度的非线性映像，但现实中必须要对隐含节点数进行确定。目前没有统一的方法对隐含层的节点数来确定，太多会降低训练速度记录非规律性的噪音，而太少会使得出的值不够准确。最常用的方法是试凑法，比较常见的经验公式主要有以下几种：、l=2n+1、，其中m为输出层节点数、n为输入层节点数、l是隐含层节点个数、a为［1，10］之间的整数。为了使BP神经网络更加准确，可进行不同节点的测试，选择学习误差最小的隐含层节点的个数。本节采用第四个计算公式，得出隐含层节点的取值范围为［4，14］，测试得出l取12时误差最小。(www.xing528.com)

BP神经网络的传递函数反应了输出与输入之间的关系，Matlab工具箱中提供了几种快速学习的算法，几种算法的比较如表3-16所示。

表3-16　典型算法性能比较表

（2）BP神经网络的设计

1）生成BP神经网络。MatlabR2010b中，生成BP神经网络的函数为newff，格式表示为：

net＝newff（minmax（normInput），［NodeNum，TypeNum］，｛TF1 TF2｝，'traingdx'）

｛TF1 TF2｝表示各层之间采用的传递函数，'traingdx'表示采用的训练函数。TF1＝'tansig'，TF2＝'tansig'。

2）定义BP神经网络各参数，如表3-17所示。

表3-17　BP神经网络参数表

在学习过程中，训练次数达到10000或者误差低于1e-2时，整个学习过程就会结束。

3）BP神经网络的学习。在MatlabR2010b中调用的函数为train，可表示为：［net，tr］＝train（net，trainSamples.P，trainSamples.T，［］，［］，validate-Samples，testSamples）。

4）BP神经网络的仿真。在MatlabR2010b中仿真调用的函数为sim，可表示为YN1＝sim（net，normInput）

3.指标体系应用评价与结果分析

（1）数据处理

根据以上对指标和数据前期进行的处理，最终选出9个输入指标和1个输出指标，随机抽取15份问卷的数据作为BP神经网络学习的基础数据。其中，I1、I2、I3、I4、I5、I6、I7、I8、I9分别代表九个输入指标；O代表动态能力这一输出指标。具体的指标值可见表3-18。

表3-18　BP神经网络学习的原始样本数据

根据上文利用Matlab对数据进行归一化处理，得到的标准化值见表3-19。

表3-19　BP神经网络学习样本数据归一化结果

（续表）

（2）Matlab运算过程

在MatlabR2010b中进行BP神经网络学习，程序编写代码如下：

（3）BP神经网络运算结果

利用15份样本数据对神经网络进行训练学习，当训练次数达到1000次时训练结束，训练曲线如图3-8所示，此时的样本均方误差是0.0067863，低于设定的误差值。

图3-8　网络训练误差变化曲线图

对网络的实际输出值和期望输出值进行线性回归分析，如图3-9所示。

图3-9　网络训练实际输出值与期望值回归分析

得到输出值与期望值的相似程度，R＝0.99267，当R＝1时表示实际输出与期望值完全吻合，图中的输出和期望值吻合度是很高的，这也表示对于网络的构建和学习是成功的，BP神经网络应用于动态能力评价是可行的。

15份样本的实际输出值、期望值及动态能力高低评级见表3-20。其中0.85≤y≤1表示优，0.7≤y＜0.85为良，0.6≤y＜0.7为中，y＜0.6为差。

表3-20　BP神经检验样本评价结果误差及评级

从表3-20结果可以看出，经过因子分析浓缩后利用BP神经网络评价的结果与期望输出基本一致，基本满足10％的误差要求，这说明因子分析与BP神经网络相结合可以用于旅游社会企业动态能力评价。

由表3-20可知，随机选取的样本中，样本8、9、10、13、15的评级属于优，说明它们的动态能力是比较强的，旅游社会企业内部管理效率高，与外部合作伙伴的沟通交流有效，各种资源得到合理利用和高效的转化，属于运营较佳的状态。1、2、3、14属于良，5、11、12属于中，说明这几家旅游社会企业的动态能力一般，资源投入和配置没有达到最佳状态，有进一步提升的空间，动态能力没有得到完全程度上的构建，应进一步采取措施提升动态能力。4、6、7则属于差的范围，说明在这些旅游社会企业中，这3家在内外部运营管理和组织架构的整合以及资源的利用等方面还有很大的提升空间。从总体来看，这些样本企业所代表的旅游社会企业动态能力高低良莠不齐，总体不高，需要采取措施对其进行提升。

总之，通过对旅游社会企业动态能力评价指标的应用来看，本书构建的评价体系结构分明，可以系统地衡量评价对象的动态能力高低，提供参考，为旅游社会企业采取措施改进并提升动态能力提供了参考性的管理建议；本书关于因子分析和BP神经网络相结合方法的引入也为动态能力评价提供了新的研究思路，丰富了能力评价的理论和方法。