债券久期即债券的有效期限和麦考利，指完全收回债券的利息和本金的加权平均年数。它反映了债券价格对利率变化的敏感性，反映了债券风险大小，可用于对债券价格的变化预测，或用于选择债券的投资管理策略。其计算公式为：
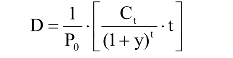
式中，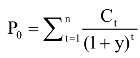
，D为债券的有效期限或麦考利久期；Ct为债券各期的现金流（利息或本金）；y为债券到期的收益率；t为任何有现金流的期数；P0为债券的现值。有时需要对久期进行修正，修正的久期计算公式为：
修正的麦考利久期=麦考利久期/（1+到期收益率）
1.DURATION（）
返回面值为100元的定期付息有价证券的麦考利久期。其格式为：
=DURATION（settlement，maturity，coupon，yld，frequency，basis）
式中，coupon为有价证券的年息票利率，yld为有价证券的年收益率。其他参数含义同前。
2.MDURATION（）
返回面值为100元的有价证券的麦考利修正期限。其公式为：
=MDURATION（settlement，maturity，coupon，yld，frequency，basis）(www.xing528.com)
式中参数含义同前。
【例4-22】 甲乙两种债券的有关资料如图4-21已知条件区域所示。那么，建立计算两种债券的有效期限的模型过程如下。
Step 1：设计模型的结构。
Step 2：在B11中输入公式“=DURATION（"2006-1-1","2016-1-1",B5,B6,B7,3）”。
Step 3：在B12中输入公式“=MDURATION（"2006-1-1","2016-1-1",B5,B6,B7,3）”。
Step 4：在D11中输入公式“=DURATION（D3,D4,D5,D6,D7,3）”。
Step 5：在D12中输入公式“=MDURATION（D3,D4,D5,D6,D7,3）”。
计算结果如图4-21所示。
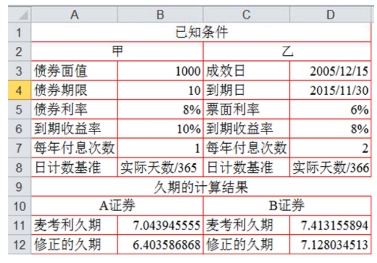
图4-21 债券久期的计算模型
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
