内部收益率（利）率函数的计算方法

当我们知道投资项目的估计现值、终值、年金、期限等情况下，需要考察投资项目的收益水平时，我们可以利用函数或单变量求解工具较方便地解决此类问题。但由于已知估计数据类型的差异，也就需要选择不同的利率函数。

1.Rate（）

返回投资期内每期现金流相等的投资项目的收益（利）率，它通过迭代法计算得出，且可能有多个解或无解。如果在进行20次迭代计算后，函数RATE的相邻两次结果没有收敛于0.0000001，将返回错误值#NUM!。其格式为：

=RATE（nper,pmt,pv,fv,type,guess）

有关参数nper、pmt、pv、fv、type的含义参见PV（）函数，其中guess为预期利率（估计值），如果省略预期利率，则假设该值为10%，如果函数RATE不收敛，则需要改变guess的值。通常情况下当guess位于0和1之间时，函数RATE是收敛的。需要注意的是，应确认所指定的guess和nper单位的一致性，对于年利率为12%的4年期贷款，如果按月支付，guess为12%/12，nper为4*12；如果按年支付，guess为12%，nper为4。

【例4-12】　公司贷款800万元，偿还期四年，每月末偿还20万元。那么银行贷款的年利率为“=RATE（4*12,-200000,8000000）*12”（图4-10）。

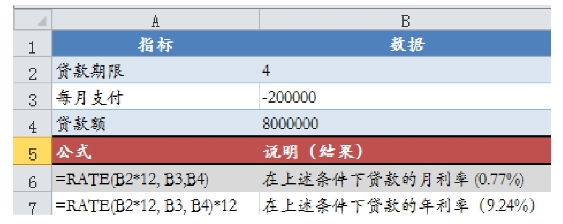
图4-10　年金偿还方式下的利率计算

2.IRR（）

在整个投资期内各期发生的现金流量不相等的情况下，无法利用RATE（）函数直接算出收益（利）率，现金流所属期间一致，则可以用IRR（）函数来解决。IRR（）函数是返回由数值代表的一组现金流的内部收益率。这些现金流不必是均衡的，它们必须按固定的间隔产生，如按月或按年。内部收益率为投资的回收利率，其中包含定期支付（负值）和定期收入（正值）。函数IRR与函数NPV（净现值函数）的关系十分密切。函数IRR计算出的收益率即净现值为0时的利率r。即

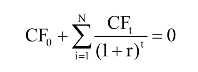
其格式为：=IRR（values，guess）。Values指现金流，通常用数组或单元格的引用，包含用来计算返回的内部收益率的数字；必须包含至少一个正值和一个负值，以计算返回的内部收益率。由于IRR（）根据数值的顺序来解释现金流的顺序。故应确定按需要的顺序输入了支付和收入的数值；如果数组或引用包含文本、逻辑值或空白单元格，这些数值将被忽略。参数Guess的含义参见RATE（）函数。

【例4-13】　龙脊山公司考虑到金融资产投资风险过高，准备年初将公司暂时闲置的资金100万元投资购买一套商品房用于出租，预计每年租金收入3.6万元，年初收取，5年后出售用于寻找新的投资机会。如果房价成长率为8%，购买时需要支付税费共计8万元，每年末维护费用0.3万元，售房时支付税费约为房价的15%，则房产投资的年报酬率为6%（图4-11）。

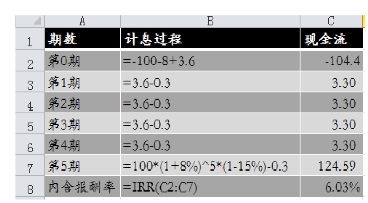
图4-11　内含报酬率的计算

3.MIRR（）

考虑再投资收益率态下的收益率，内部报酬率假定现金流入而产生的再投资也就是在内部报酬率下进行的，同时这种报酬率没有考虑融资成本。显然，这种前提在很多情况下并不成立。而且，由于投资期的现金流并不一定按投资时现金流为负、投资后的现金流全部为正的规则进行，故可能出现内部收益率无法收敛或出现多解的情况。为了解决IRR（）求内部收益率的缺陷，我们可以用修正的内部报酬率函数MIRR（），用来返回连续期间内现金流的修正内部收益率。函数MIRR考虑了投资的成本和现金再投资的收益率。其格式为：

=MIRR（values，finance_rate，reinvest_rate）

Values的含义参见IRR（）函数。Finance_rate指现金流中使用的资金支付的利率；Reinvest_rate则是将现金流再投资的收益率。

需要补充说明的是：

①函数MIRR根据输入值的次序来解释现金流的次序。所以，务必按照实际的顺序输入支出和收入数额，并使用正确的正负号（现金流入用正值，现金流出用负值）。

②如果现金流的次数为n，finance_rate为frate而reinvest_rate为rrate，则函数MIRR的计算公式为：

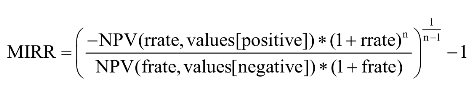
【例4-14】　龙脊山公司拟投资12万元购进一台新设备，通过测算估计新设备使用的五年期间能够带来的现金流分别为39 000元、30 000元、21 000元、37 000元和46 000元。由于公司自有资金紧张，考虑以10%的利率从银行借入该设备款项，投资期间再投资收益率估计为12%。那么再投资收益率的计算则可用MIRR函数求得（图4-12）。

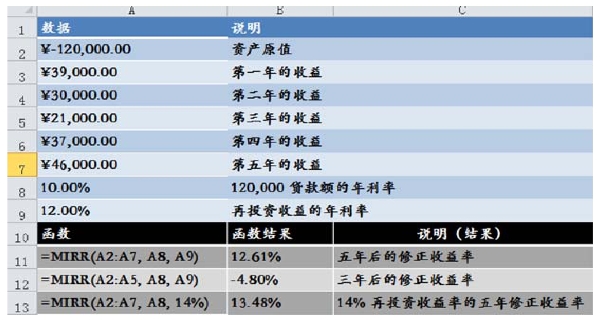
图4-12　修正的内含投资收益率的计算

4.XIRR（）

投资期内现金流、所属期间不等状态下的收益率。在整个投资期内各期发生的现金流量所属期间不相等的情况下，无法利用IRR（）函数直接算出利率，则可以用XIRR（）函数来解决。XIRR函数是返回由数值代表的一组现金流的内部收益率，这些现金流不一定定期发生。其格式为：(www.xing528.com)

=XIRR（values，dates，[guess]）

Values是与dates中的支付时间相对应的一系列现金流。首期支付是可选的，并与投资开始时的成本或支付有关。如果第一个值是成本或支付，则它必须是负值。所有后续支付都基于365天/年贴现。值系列中必须至少包含一个正值和一个负值。Date是与现金流支付相对应的支付日期表。日期可按任何顺序排列。应使用DATE函数输入日期，或者将函数作为其他公式或函数的结果输入。例如，使用函数DATE（2008,5,23）输入2008年5月23日。如果日期以文本形式输入，则会出现问题。Guess是对函数XIRR计算结果的估计值，可以不选。

需要补充说明以下几点。

①Microsoft Excel可将日期存储为可用于计算的序列数。默认情况下，1900年1月1日的序列号是1，而2008年1月1日的序列号是39 448，这是因为它距1900年1月1日有39 448天。

②Dates中的数值将被截尾取整。

③函数XIRR要求至少有一个正现金流和一个负现金流，否则函数XIRR返回错误值#NUM!。

④如果dates中的任一数值不是合法日期，函数XIRR返回错误值#VALUE!。

⑤如果dates中的任一数字先于开始日期，函数XIRR返回错误值#NUM!。

⑥如果values和dates所含数值的数目不同，函数XIRR返回错误值#NUM!。

⑦多数情况下，不必为函数XIRR的计算提供guess值，如果省略，guess值假定为0.1（10%）。

⑧函数XIRR与净现值函数XNPV密切相关。函数XIRR计算的收益率即为函数XNPV=0时的利率。Excel使用迭代法计算函数XIRR。通过改变收益率（从guess开始），不断修正计算结果，直至其精度小于0.000001%。如果函数XIRR运算100次，仍未找到结果，则返回错误值#NUM!。函数XIRR的计算公式如下：

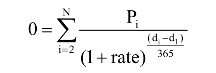
式中，di是第i个或最后一个支付日期；d1是第0个支付日期；Pi是第i个或最后一个支付金额。

Excel 2003及以下版本需要在加载“加载宏”里的“分析工具库”方可使用。

【例4-15】　龙脊山公司近几年利用暂时不用销售收入进行不定期的证券投资，其投资和收回投资的时期及对应金额如图4-13中A81:B86所示。在B87单元格中输入公式“=XIRR（B81:B86,A81:A86）”回车确认即可得到其收益率为40.71%。当然，我们也可以在单元格B88中输入公式“=XNPV（B87,B81:B86,A81:A86）”进行验证，此时净现值为0，表明内含报酬率的计息结果正确。

5.RRI（）

返回投资增长的等效利率。其格式为：=RRI（nper，pv，fv）。

RRI使用以下公式，用给定的nper（期数）、pv（现值）和fv（未来值）计算利率的返回值：

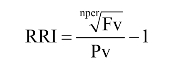
需要补充说明的是：

①如果参数值无效，则RRI返回错误值#NUM!。

②如果参数没有使用有效的数据类型，则RRI返回错误值#VALUE!。

【例4-16】　龙脊山公司购买了15万元10年债券，债券到期后连本带利一次性可回收18万元。则年收益额的计算如图4-14中C3单元格的计算所示。

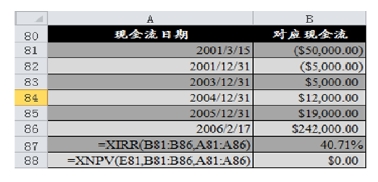
图4-13　现金流量不规则的收益率

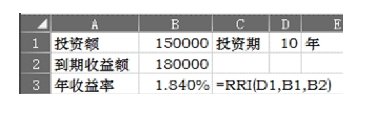
图4-14　投资增长的等效利率