利率不变情况下的终值计算方法

现金流量稳定、利率不变且各期现金流量所属时间相等的情况下，考虑现金流量的期数、计息的方式不同，主要分为以下情况。

复利终值：F=P·（1+i）n　或　F=P·（FVIFi，n）

单利终值：F=P·（1+i·n）

普通年金终值：或F=A·（FVIFAi，n）

先付年金终值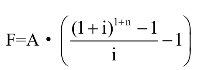：或F=A·（FVIFAi，n）·（1+i）

式中，F、P分别代表终值和现值，i代表利率，FVIFi，n、FVIFAi，n分别为复利终值系数和年金终值系数。(www.xing528.com)

在Excel中计算终值可用上述公式，也可以利用函数FV（）来完成。其格式为：

=FV（rate，nper，pmt，pv，type）

函数的功能就是计算未来若干期资金的终值。rate为各期利率；nper为总投资期（即该项投资的付款期总数）；pmt为各期所应支付的金额，其数值在整个年金期间保持不变；pv为现值（即从该项投资开始计算时已经入账的款项，或一系列未来付款的当前值的累积和，也称为本金）。如果忽略pmt，则必须包含pv参数，即求复利终值。如果省略pv，则假设其值为零（一笔贷款的未来值即为零），则必须包含pmt参数，即求年金终值。Type为0时指期末，1为期初。

【例4-6】　假如现在存入100万元，年利率为5.78%（单利计息）的情况下，五年后可以取得的金额为“=FV（5*5.78%,1,,-100）”；如为复利计息，现在可以取出的金额为“=FV（5.78%,5,,-100）”；如果在未来的五年每年年末/初存款100万元，年利率仍然为5.78%，那么五年终了可以取得的金额为“=FV（5.78%,5,-100,，0）”/“=FV（5.78%,5,-100,，1）”（图4-6）。

【例4-7】　假设需要为一年后的一项工程预筹资金，现在将2000元以年利4.5%，按月计息（月利为4.5%/12）存入储蓄存款账户中，并在以后十二个月的每个月初存入200元。那么一年后该账户的存款额为：=FV（4.5%/12，12,-200,-2000,1）。计算结果为4551.19元（图4-6）。