发电权交易利润分配模型优化方案

如何分配发电权交易利润是发电权交易模式设计的关键。由于发电权交易的实质可视为不同类型的机组之间（如水电与火电、大火电与小火电等）通过电量置换实现合作上的“共赢”，上述问题就可归结为合作利润如何在它们之间进行分配的问题，这可运用合作博弈的理论进行分析。合作博弈是博弈论的一个重要分支，主要研究多人如何进行合作达到联盟利益的最大化以及联盟利益如何在他们之间进行分配，被广泛应用于合作利润分配和成本分摊中。

本小节将机组之间的发电权交易视为一种合作博弈行为，运用合作博弈理论设计机组的合作利润分配机制。

当参与合作能够使得合作人较不合作之前获得更多利润的时候，参与人就会选择合作，而每个参与合作的人都希望能从合作中分配得到满意的利润，因而如何设计一套合理的分配机制就是合作博弈的一个研究重点。核心法和Shapley值法是合作博弈中常用的两种利益分配方法。

3.3.2.1　核心法分配模型

1.核

设集合N={1，2，…，n}，如果对于N的任一子集S（表示n人集合中的任一组合）都对应着一个实值函数V（S），满足V（φ）=0，V（S1∪S2）≥V（S1）+V（S2），其中S1∩S2=φ，则称[N，V]为n人合作对策，V为对策的特征函数，V（S）称为合作联盟S的收益值。

用Xi表示N中第i个成员从合作的最大效益值V（N）中应得到的一份收入。则X=（X1，X2，…，Xn）称为合作博弈对策的分配策略。如果X满足如下3个特性：

（1）整体合理性：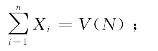

（2）个体合理性：Xi≥V（i），∀i∈N，其中V（i）是成员i不与其他成员结盟时的收益；

（3）联盟合理性：

则称分配X为该合作博弈的核，记为C（V）。

2.核心法

一个合作博弈的核可能是空集，此时解决该合作利益分配问题的方法是给该合作模型中的联盟和理性条件加一松弛变量。按照给联盟S的收益V（S）所加额外量的方法不同，核心法可分为最小核心法和比例最小核心法。

在最小核心法中，给所有联盟S的联盟收益总和都加一个相同的额外量ε，计算联盟各成员的分配收益即为求解以下线性规划问题(www.xing528.com)

在比例最小核心法中，给联盟S的联盟收益增加一个与其开发收益总和成比例的额外量来求解核心，因此所求解的线性规划问题为

3.3.2.2　Shapley值法分配模型

Shapley值满足以下3个特性。

（1）有效性。如果对于所有包含了i的子集，均有V（S-i）=V（S），则有Xi（V）=0，且有。此性质表示：如果成员对于每一个它参加的合作都没有贡献，则它不应该从全体合作的收益中获得报酬；其次，各个成员的收益值和应该等于其总收益。

（2）对称性。设π是N={1，2，…，n}的一个排列，即N为到它自身的对应，若πi为i的对应，πs为S的对应（S⊂N）；记V（πs）=U（S），则对于一切i=1，2，…，n有。此特性表示，每个人的分配与它被赋予的记号i无关，即位置对称性。

（3）可加性。对于定义在N上的任意2个特征函数U和V，有Xi（U+V）=Xi（U）+Xi（V），其中i=1，2，…，n。此性质说明，当n人同时进行两项合作时，该收益应该为2项合作的分配之和。

给出了上述性质之后，Shapley提出了计算合作对策利益分配的共识。即Shapley值由特征函数V确定，记作X=（X1，X2，…Xn），称为合作博弈的分配策略，其中Xi为

式中　Si——N个包含了i的子集；

|S|——子集S中的元素个数；

W（|S|）——加权因子；

V（S）——包含i的联盟S的合作收益；

V（S-i）——不包含i的联盟收益。