直方图是以一组无间隔的直条图表现频数分布特征的统计图,也是表示数据变化情况的一种工具。将测定值的存在范围分成几个区间,每个区间为底边,然后以这个区间所测定值出现次数的比例面积排列成长方形图,因此称为直方图。通过直方图可以容易看出计量值的数据分布状况(如成绩、故障次数、次品数),利用分析数据的规则性尤其是中心值和分布状况等信息来掌握问题点,以选择进行改善对策。在生产中可以比较直观地了解产品质量的分布状态并判断工序是否处于受控状态,还可以对总体进行判断,分析其质量分布情况。
直方图是一种特殊的条形图,单个的数据点按类分组,因此可以了解每一类数据发生的频率。高的条显示某类的件数更多,而低的条则表示较少的件数。在如图3-6 所示的直方图中,其峰值在308.5类处有13件。
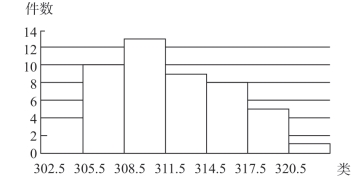
图3-6 直方图示意
直方图的优点是它提供了一种直观表达的数据集的位置和变化,但有较明显的缺点。当类的划分方式不同时,直方图有可能被制成完全不同的图。比如,使用过少或过多条时,直方图都可能有意无意地产生误导。这是一个需要判断而且还部分需要试验的领域,能否正确使用主要取决于分析人员的经验。直方图的条数(组数)与总数据数量有关,一般对数据的分组可参考表3-9。
表3-9 数据的分组


组距的计算如式(3-2)所示,一般取2,5或10的倍数。
最小一组的下组界=最小值-测定值的最小位数/2;最小一组的上组界=下组界+组距。
直方图可能使数据集内的时间差别模糊。在质量控制中,一个流程的直方图告诉人们的只是一个长期过程中的一部分。因此,有必要不断回顾以前的多个直方图,并将直方图和具有一段时期持续性的控制图结合起来使用,以获得工艺控制方面的知识。
1.直方图可以计算的统计量
直方图制作完成后,要通过各区域参数呈现出来的直条图进行统计数据分析,这些可以计算的统计量如下。
①平均值:所有值的平均值。
②最小值/最大值:最小的数值/最大的数值。
③标准差:表示测量值围绕平均值的波动大小。
④类宽:直方图中每条左右之间的X轴距离。
⑤类数:直方图中条的数目(含零高条)。
⑥斜度:若直方图对称则偏斜为0。若左边尾更长,偏斜为负值;若右边尾更长,偏斜为正值。当存在偏斜时,作业能力指数值得推敲。为改进作业流程,应首先关注分布的长尾部分,此处通常是发生质量问题的地方。
⑦峰度:峰度是分布尖锐程度的量度。标准曲线的峰度值为0。尖锐的峰为负峰度;而平曲线则为正峰度。负峰度的作业流程较受欢迎,而正峰度通常存在更多问题,需要进行质量控制,因为尾巴大,可能意味着作业流程比波动规范限制的范围要宽。
2.规范限制和批质量
在相关的地方,可以在直方图上显示规范限制。规范应包括目标值、一个上界限和一个下界限。
通过将规范限制叠加到直方图上,可以估计有多少产品不符合规范要求。这同时也可以了解到整个批次产品的质量,即在搜集数据期间作业实际状况如何。若使用相应的软件还能够同时获得落到规范范围外的产品数量比例。
也就是说,只要在直方图上加上目标值、上下界限,就可以通过直方图来检验作业流程的实际状况如何,如图3-7所示。
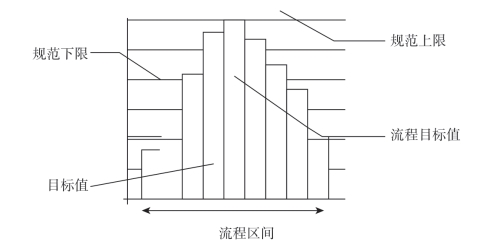
图3-7 直方图区间示意
若直方图显示流程大于规范的限制范围,就意味着需要采取措施来减少作业流程的波动范围。若作业流程不是以目标值为中心波动,也可能需要将其调整到目标值。若流程出现中心偏差,也常常会使得产品的波动范围向某一方向上越界。
直方图有许多指标来描述其特征,以下分别加以介绍。
(1)分布的中心
当作业流程稳定时应该有一个目标值,且大多数的产品(也即分布的中心)会落在该值上或其附近,否则该流程就需要加以调整了。
(2)分布的范围
流程分布的范围或宽度是指测量的最小值和最大值间的距离。若分布小于规范限制的范围,说明作业波动较小。在大多数作业流程中一致性都很重要,通常这也是流程控制的一个重要目标。如果分布大于波动规范的要求,则作业流程就会产生出不符合要求的产品。
(3)形状(https://www.xing528.com)
常规的变化分布应该显示为高点在中间且在中心两侧呈平滑对称倾斜下降的钟形曲线。在实际作业过程中,当作业流程处于非常规状态时会出现各式各样的非常规分布,其中有歪斜的、平的或比常规分布更尖的峰。
歪斜的分布是不对称的,而在某一方向有一长尾。若长尾伸向右侧则曲线称为右斜或正倾斜(+);若长尾伸向左侧则曲线称为左斜或负倾斜(-)。
峰度是分布居长的量度。比如,具有正峰度的对称分布表示其尾部的产品多于常规比例,而负峰度的曲线具有比常规分布曲线短的尾部。
总之,作业流程的中心值、宽度、偏斜度、峰度可以提供很多有关作业流程的信息。但对于不是很了解统计学原理的作业人员来说,从直方图中也许可以得到的信息更多。
作业流程中许多重要的信息都是来自对于规范限制附近的局部数据的研究(即生产出现不一致的产品)。
3.常见的形状
直方图因频数、区间等参数的设置不同,其形状也有差异,即便参数设置合理,呈现出来的图形也多种多样,但比较常见的有以下几种。
(1)标准常规分布曲线
标准常规分布曲线的特征是具有零偏斜和零峰度,如图3-8 所示。
直方图的直方形以中间为顶峰,向两边大体对称排列,这属于正常的分布图。
(2)偏斜形分布曲线
偏斜形分布曲线的特征是一个尾部比另一个长,如图3-9所示。
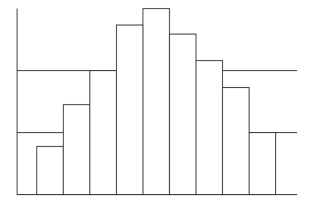
图3-8 标准形直方图
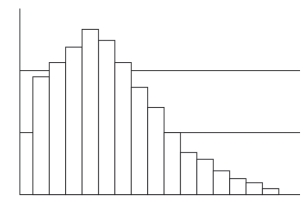
图3-9 偏斜形直方图
其高峰位于一侧,另一侧呈下降缓坡形态。在正常情况下,通常是由于产品的公差(标准)是单侧或某种加工习惯等原因所造成的。如只有公差上限要求的产品,其质量分布往往会右偏;只有公差下限要求的产品,其产品的质量分布往往会往左偏。
(3)双峰形曲线
双峰形曲线,如图3-10所示。此形态通常是由于数据来自两个具有不同中心值的作业流程。要反映各个流程自己的特性,应该将两个流程区分开来。其原因可能是将有一定差别的两台设备或两种不同的原料所生产的同类型产品混合在一起统计造成的,这时应先按照数据的不同性质将其进行分离,然后再进行直方图分析。
(4)删节形曲线
删节形曲线如图3-11所示,其峰为边或位于边附近,而另一侧则呈逐渐下降形态,通常是由于分布形态的一部分经过筛选、全部检查或返工后而被移去。此类作业方式通常成本高,需要进一步地改进。
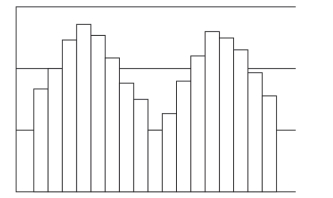
图3-10 双峰形直方图
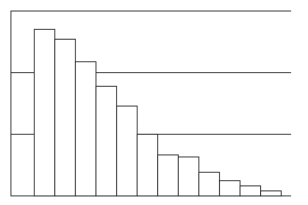
图3-11 删节形直方图
(5)平顶形曲线
平顶形曲线如图3-12所示。这种直方图顶部平直、无明显的峰谷。出现这种图形的原因主要是由于作业流程能很好地说明清楚,流程作业时作业人员有较大的随意性而产生了此种结果。因此急需制定一个统一的作业标准。
(6)孤岛形分布曲线
孤岛形分布曲线如图3-13所示,一组条距离其他组条至少有一个条宽,通常是由于在作业过程中有一个独立的作业流程加入进来,但这种情况并不是经常出现的。也可能是由于流程中出现了特殊的变动,在此种情形下则应进行调查。对于由于原材料的变化、短期内由不熟练员工替班作业、测量有误等原因产生的此类情形应尽量采取措施避免。
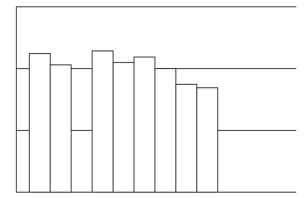
图3-12 平顶形直方图
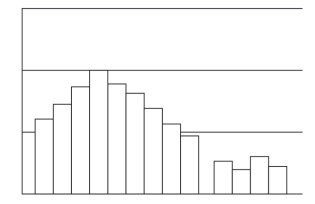
图3-13 孤岛形直方图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




