多项式回归的原理解析

十几年来,两个构念间的匹配和一致性研究在微观和宏观层面的组织研究中受到越来越多的关注(唐杰等,2011;Edwards,2007)。在衡量两个构念间的匹配程度时,绝大部分研究都采用了差异分数法,用|X-Y|或(X-Y)2进行刻画。然而,差异分数法虽然应用广泛,却存在以下缺陷:首先,应用差异分数法时虽然两个测量变量的单独信度都高,但是用两个测量变量差值的绝对值代表匹配或一致程度会使信度和效度降低(Johns,1981);其次,差异分数对非对称效应(高低、低高)难以刻画和解释,因此很难检验一些在匹配研究中有重要意义的假设内容(EdwardsandCable,2009);再次,应用差异分数法,对两个测量变量的一次项或二次项系数均存在较为严苛的约束条件,往往超出了匹配理论本身所包含的内容。

为了避免这些问题,有学者提出了通过建立多项式回归方程,评价两个自变量的组合(匹配及一致性程度)对结果变量的影响,并借助响应面分析(responsesurfaceanalysis)将统计检验结果绘制成三维图像,立体展现匹配及一致性效应(Edwards and Parry,1993)。该方法对差异分数法中用两个测量变量差值的绝对值或平方项来描述一致性的回归方程进行代数转换,释放了对系数严格而不必要的约束并补充两个测量变量的一次项,得到如下回归方程:

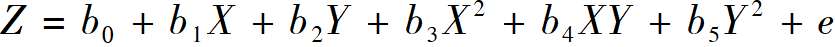(5.3)

比较上述三个回归方程可发现,多项式回归方程(式5.3)是完整意义上的二次多项式,并释放了差异分数法中缺乏二次项,或X2与Y2系数相同、为XY系数的-1/2、且X和Y系数为0的约束条件。这使得该方法的应用条件更宽松,研究边界更广。同时,多项式回归方程分别估计了构成一致性效应的两个自变量与因变量间线性和非线性的关系,以及两个自变量的交互项与因变量间的线性关系,解释力更强。简而言之,该方法较之差异分数法,无论在方法的规范性还是实际应用意义上都更具优势。(www.xing528.com)

多项式回归可以解释下列问题:两个预测变量之间的差异度对因变量的影响;两个预测变量之间的一致程度对因变量的影响(两个变量高-高匹配和低-低匹配对因变量的影响差异如何);两个预测变量不一致的方向如何影响因变量(两个变量不匹配时哪一种不一致的影响更大)。近20年来,这种方法得到了国内外学者(Kalliathetal.,1999;Cohenetal.,2003;Ostroffetal.,2005;Gibsonetal.,2009;陈卫旗,2009;龙立荣、赵慧娟,2009)的认可,广泛应用于组织行为学的一致性问题研究和匹配研究等领域,相关研究成果在AMJ、JOB、JAP及《管理世界》《心理学报》等国内外权威期刊上发表。

当然,使用该方法需要满足下列假设前提(Edwards,2007):首先,两个自变量来自同一个概念域;其次,两个自变量的量纲必须相同,这样它们的一致性(匹配)程度才可以被有效测算;再次,作为一种回归分析方法,需要满足基本的回归诊断要求。