如何进行Excel风险衡量？

风险与概率直接相关，并与期望值、离散程度相联系。离散程度是用以衡量风险大小的统计指标，主要包括方差、标准离差、标准离差率等。一般来说，离散程度越大，风险越大；离散程度越小，风险越小。其中方差、标准离差是绝对数，只适用于期望值相同的方案比较；标准离差率是相对数，可用于各种方案比较。

1.投资风险指标的计算

期望值又称期望收益，是指某项投资未来收益的各种可能结果，它以概率为权数计算加权平均数，是加权平均的中间值，用表示；方差是表示随机变量与期望值之间的离散程度的一个数值，用σ2表示；标准离差也称均方差，是方差的平方根，用σ表示；标准离差率又称变异系数，是标准离差与期望值之比，用V表示。投资风险指标计算公式如下：

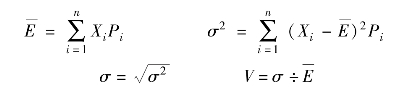
式中，Xi表示第i种随机事件的结果；Pi表示第i种随机事件发生的可能性，各种随机事件发生可能性之和应等于1。

2.Excel幂运算

Excel计算乘方时可用＾运算符，也可用如下幂函数计算：

＝POWER(number，power)

式中，number表示底数；power表示指数（幂值），平方为2、立方为3等。

3.Excel平方根运算

Excel计算平方根可用＾运算符，也可用如下平方根函数公式计算：

＝SQRT(number)

式中，number表示需计算平方根的数据，该参数不能为负值。

某公司的投资项目有A、B两个方案可供选择，A方案投资额80万元，B方案投资额100万元。经预测分析，投资后的宏观经济情况可能为繁荣、正常和衰退，这些情况出现的可能性（概率）和投资收益情况见表3-1。

表3-1　某公司投资项目分析数据

Excel中完成的风险分析如图3-5所示。

（1）录入A1、A2、A3、A5至A12、G2、B3、C3、F3、C4至H4单元格的文本字符；合并单元区域，设置边框、字体字号，调整行高列宽等。(www.xing528.com)

其中，录入行标题的文本公式“（Xi-E）2∗Pi”，要使用上标、下标。此时，可先在单元格中录入“（Xi-E）2∗Pi”，选定要作下标的字符“i”，右击选择并进入“设置单元格格式”对话框，如图3-6所示，勾选下部的“下标”复选框。

（2）录入已知数值。在B5至C7、F5至F7单元区域录入概率、收益率数据。

（3）计算期望收益率。在D5单元格输入“＝B5∗C5”，通过D5单元格的填充柄自动填入D6、D7单元格公式。选定C8单元格，单击自动求和按钮，并将公式修改为“＝SUM（D5：D7）”。

图3-5　风险分析结果（Excel 97）

图3-6　设置字体下标（上标）对话框

用类似的方法录入G5至G7单元区域公式、F8单元公式。

（4）用公式计算A方案指标：选定E5单元格，输入公式“＝（C5-＄C＄8）＾2∗B5”；其中，“＄C＄8”为绝对引用C8单元格，可先输入（或单击引用）“C8”，再按下键盘上的“F4”键。通过E5单元格的填充柄，自动填充E6、E7单元格公式。

在C9单元格（方差）中输入公式“＝SUM（E5：E7）”；在C10单元格（标准离差）中输入求平方根公式“＝C9＾（1/2）”；在C11单元格（标准离差率）中输入相除公式“＝C10/C8”。

（5）用函数计算B方案指标：选定H5单元格，单击插入函数按钮，选择“数学与三角函数”类别中的幂POWER函数进入函数参数对话框，如图3-7（a）所示；键入幂底“F5-＄F＄8”，幂值“2”；单击“确定”按钮后H5单元格显示“＝POWER（F5-＄F＄8，2）”；在公式后部再键入“∗B5”。

F10单元的平方根函数与幂函数使用方法类似，只是在“数学与三角函数”类别中，选择平方根函数SQRT进入函数参数对话框，如图3-7（b）所示；在参数中键入“F9”。

图3-7　幂POWER（a）与平均根SQRT（b）函数对话框

（6）条件IF函数比较风险。在C12单元格中，输入条件函数公式“＝IF（C11>F11，"A风险大"，IF（C11＝F11，"风险相同"，"B风险大"））”。

含义：若C11大于F11值，则A风险大；若两者相等，则风险相同；否则为B风险大。

（7）显示单元公式。默认情况下，单元格中显示运算结果，编辑框中显示公式。若需要在工作表的单元格中显示公式，如图3-8所示，可在英文输入状态下，在键盘上使用组合键“Ctrl＋～”（即按下“Ctrl”键的同时按下“～”键）；再使用组合键“Ctrl＋～”，则各单元格将显示计算结果。

图3-8　风险分析显示公式（Excel 2019页面布局选项卡）

（1）Excel 2007—Excel 2019用命令显示单元格公式：单击“公式/公式审核/显示公式”按钮，则单元格显示公式。再次单击，则单元格显示运算结果。

（2）Excel 2003及其以前版本用命令显示单元格公式：选择“工具/选项”菜单命令，选定弹出对话框的“视图”卡片，勾选其中的“公式”复选框。若去掉此复选框，则单元格中显示计算结果，编辑框中显示单元公式。