应急物资补充与订购——仿真模拟雅安地震案例

在雅安地震发生后，应急部门发现预先存储的应急物资数量不能满足救灾的需要，所以决定补充征购一批物资。政府工作人员通过“重大突发事件应急物资筹运的决策支持平台”中的“物资征购辅助”模块在政府官方网站中发布应急物资的补充征购信息，并且主动与数据库中的目标供应商取得联系，以确认其供应能力和意愿。在找到合适的供应商之后，政府即刻与之就应急物资的价格和质量进行谈判。政府在与供应商谈判的时候，应该遵循本书给出的“WRAD”原则，即(1)确保给出的低价不能过低；(2)拉开给出的高价与低价之间的距离；(3)在选择供应商并依次进行谈判时，应遵循“从大到小选择，从小到大谈判”的原则。在时间充裕，相关数据比较容易获得的情况下，政府可以根据前面的算法计算出最优的高价和低价，以及与各个供应商成功谈判的概率。

假设在救灾过程中，政府发现缺少10000顶应急帐篷，需要紧急向供应商征购。帐篷有高质量和低质量的两种类型，其成本分别为2万元和1万元。由于供应商需要紧急加班调货和生产，所以需要支付给工人固定加班费1万元。如果帐篷因为质量不合格而无法使用，政府需要额外支付2万元以更换其他帐篷。高质量的帐篷不合格的概率为0.1；低质量的帐篷不合格的概率为0.2。如果政府决定不跟当前的供应商合作而寻找其他供应商，会浪费一定的救援时间，造成的经济损失折合30万元。高质量的帐篷比低质量的帐篷更能有效保证灾民的安全生活，而顺利救助灾民也可以看成政府的收益，则两种帐篷给政府带来的收益折合50万元和40万元。在政府给出高价的情况下，供应商对于该交易更加积极，从而供货速度会较政府给出低价的情况高。本部分将这两种供货速度转换为帐篷的实际救援效果的系数，分别设为1和0.7。各种情况下的交易概率系数设为g1＝0.8，g2＝0.9，g3＝0.1。为了方便计算，假设共有10家供应商，它们之间只有供应能力不同，其供应能力分别为4000，3700，3300，3000，2700，2300，2000，1700，1300，1000。将它们依次编号为1，2，…，10号。

在此案例中，由于前三个供应商的供给能力总和恰好超过需求量，所以政府首先依次与3号、2号和1号供应商谈判。基于政府需要以低价格购入高质量的帐篷的方针，根据前面的算法求得政府第一轮谈判的最优高价和低价，以及各个供应商的成功谈判的概率，如表7-2所示。

表7-2　第一轮谈判计算结果

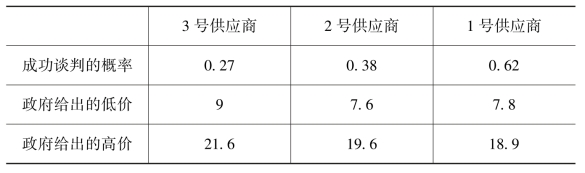
假设在第一轮谈判之后，政府与2号和3号供应商的谈判失败，而仅与1号供应商的谈判成功。所以政府必须进行第二轮谈判，由于此时帐篷的供应缺口为70，所以政府再选择4号、5号和6号供应商，再依次与6号、5号和4号供应商谈判。同理可算得政府第二轮谈判的计算结果，如表7-3所示。

如果该轮谈判仍然没有满足需求，则进行下一轮的谈判，相应的政府谈判的最优高价和低价，以及各个供应商的成功谈判的概率，按照上述方法可以求得。

表7-3　第二轮谈判计算结果

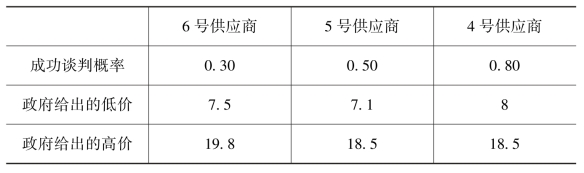
在这个过程中，假设政府对某个供应商给出两种购买价格，分别是10万元和5万元；政府出高价且供应商选择提供高质量的帐篷时，或政府出低价且供应商选择提供低质量的帐篷时，物资交易成功率为0.6；政府出低价且供应商选择提供高质量的帐篷时，物资交易成功率为0.8；政府出高价且供应商选择提供低质量的帐篷时，物资交易成功率为0.2。

此时，因为：

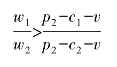
所以有纳什均衡解：

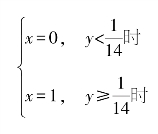
又因为：

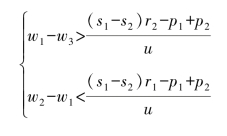
所以有纳什均衡解：

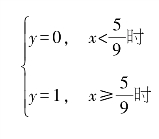
所以，可以画出供应商和政府进化博弈的复制动态和稳定性关系图，如图7-7所示。由该图可知，如果博弈的初始值落入矩形OABC中，那么其进化稳定策略为(0，0)；如果博弈的初始值落入矩形BDFE中，那么进化稳定策略为(1，1)。

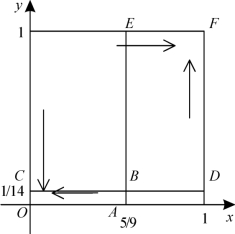
图7-7　供应商和政府的进化博弈复制动态和稳定性

接下来对政府和供应商的议价博弈过程进行仿真。设供应商和政府在初始时刻对于交易是否成功没有倾向性，即x＝0.5；y＝0.5。系统的仿真结果如图7-8所示，从图中可以清楚的看到最终的博弈结果是政府给出高价且供应商提供高质量的帐篷。从图中两条曲线的走势，可以做出如下分析：对于供应商来说，其做出“提供高质量的帐篷”的选择始终没有改变。对于政府来说，在一开始却倾向于做出“给出低价”的选择，但经过短暂犹豫后，立刻改变主意给出高价。并且政府对于“给出高价”这个决策的坚定程度甚至还超过了供应商对于“提供高质量的帐篷”的决策。此结果可以解释为，供应商首先表现出了提供高质量的帐篷的意愿倾向，但还未最终确定；政府一开始不知道供应商会提供什么质量的帐篷时，倾向于给出低价以控制财政支出，但获知供应商愿意提供高质量的帐篷的信息后，政府立刻改变策略，给出高价以鼓励其提供高质量的帐篷。最终，双方达成共识，政府给出高价购买供应商的高质量帐篷。(www.xing528.com)

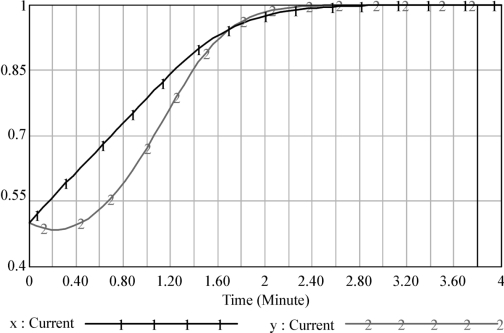
图7-8　应急物资补充征购谈判仿真结果

同时，政府工作人员利用“重大突发事件应急物资筹运的决策支持平台”中的“物资需求预测”模块对震后72小时以内的帐篷、棉被和饮用水的订购、供给和运输情况进行大致仿真，系统参数根据实际情况设置。下面将仿真结果跟实际数据进行比对。

(1)对帐篷的订购、供给和运输仿真情况如图7-9所示。实际的供应情况与仿真情况对比，如表7-4所示。

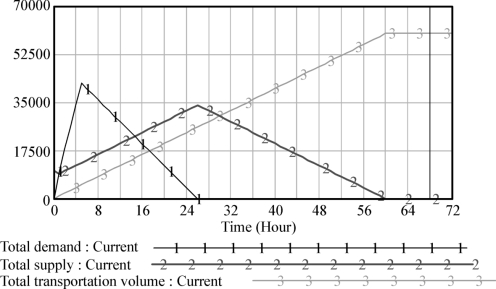
图7-9　帐篷的补充征购情况仿真

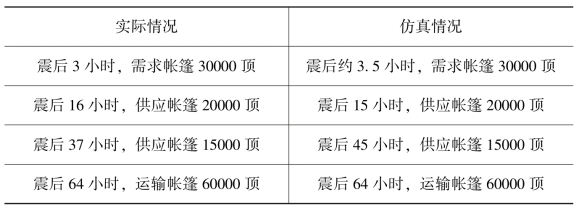
表7-4　帐篷的补充征购数据对比

(2)对棉被的订购、供给和运输仿真情况如图7-10所示。实际的供应情况与仿真情况对比，如表7-5所示。

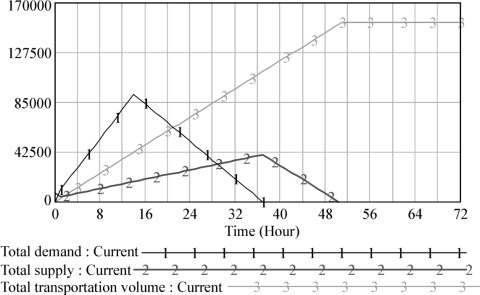
图7-10　棉被的补充征购情况仿真

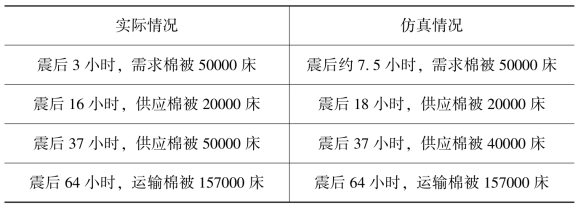
表7-5　棉被的补充征购数据对比

(3)对饮用水的订购、供给和运输仿真情况如图7-11所示。实际的供应情况与仿真情况对比，如表7-6所示。

表7-6　饮用水的补充征购数据对比

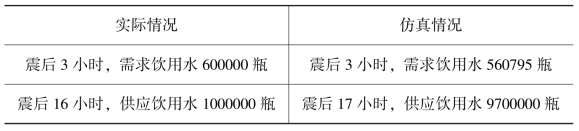
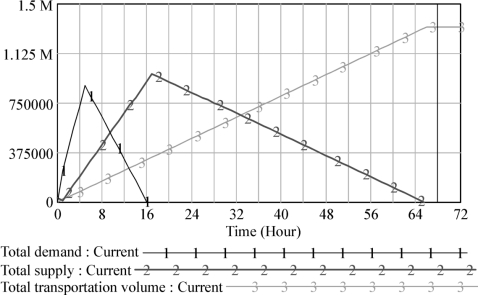
图7-11　饮用水的补充征购情况仿真

续表

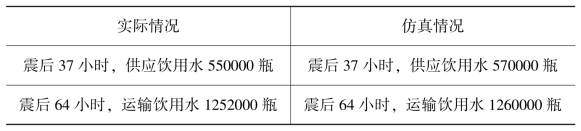
从以上的仿真结果可以看出，利用本书提出的突发事件应急物资补充征购模型预测的数据基本实际数据吻合。从而政府工作人员可以根据此预测数据大致确定在当前情况下，政府应急物资的拥有量是否可以满足救灾需求。