突发事件应急物资准备、调度和运输的工作流程系统优化方案

应急物资的准备流程、调度流程和运输流程是一个整体系统。只有当它们很好地协调时，应急物资才可能在最短的时间内抵达灾区。因此，研究整个决策流程的优化方法，对提高应急物资的调度效率帮助很大。在突发事件发生后，决策者必须在很短的时间内对整个物资准备与调度流程进行分析，以缩短流程中的排队等待时间。而缩短整体流程的排队等待时间必须从缩短各个环节的排队等待时间着手。这个时候，各个环节的事件发生时间往往不相互独立，也不服从一个确定的分布，所以用传统的排队论模型计算起来就会十分复杂。特别在应急决策的前提下，更是没有时间进行计算。基于Petri网的工作流系统仿真就是解决此问题的一个非常有效的方法(Moscato et al.，2012；Hiraishi，2008；Yamaguchi et al.，2001)。它不但能检测整个流程的正确性，而且能够仿真出流程各个环节的细节参数(Van der Aalst，1998)，更可以分析系统中的有限资源的应用情况(Wang，2009)。例如，Wang(2012)用基于Petri网的工作流系统对紧急救护流程中有限资源的应用进行了优化。整合应急物资的准备、调度、决策等诸多方面于一个系统，并对其进行分析优化的研究比较缺乏，而将这个系统通过编程实现更是少有研究涉及。但是，建立这样一个决策支持系统却能够很好地帮助政府在重大突发事件中对应急物资进行有效的筹运。

在确定了突发事件应急物资准备、调度和运输的流程后，若能得知该流程中每个环节的耗时量，就能找出提高整个流程运行速度的方法。因为在一次事件中，每次应急物资的需求信息到来后，政府就要启动该程序对应急物资进行准备、调度和运输，故该流程会执行很多遍，且时间跨度很长。同时，该流程中的大多数环节运行所需的资源，如工作人员，都是明确的、有限的。所以，这就为利用工作流仿真系统对其分析提供了前提条件。

在应急物资运输的过程中，每辆车都从集散地装载物资后，就依次运往各个受灾地，待所载的应急物资卸完之后，再回到集散地装载新的物资继续运输。那么，根据第4章提出的“重大突发事件应急物资运输调度的模型”就可以计算出车辆到达(返回)集散地的间隔时间。显然，为了使整个流程不间断地运行，准备与调度物资的工作应该在这段时间内完成，从而保证下一辆车到达集散地之后有货可装，且有明确的运送目的地。其中，最好的情况是当前批的物资已经在前面准备好，只需调度；最坏的情况是当前批的物资完全没有准备，故必须一次完成物资准备和调度两个任务。显然，最坏的情况对物资准备和调度任务的要求更加严格。为了保证系统的流畅运行，下面的研究将基于上述最坏的情况。

设车辆k＋1和车辆k返回集散地的时间分别为tk＋1和tk，且车辆k＋1在车辆k之后返回，二车之间没有其他车辆。则其时间间隔为tk＋1-tk。再设参与运输的车辆总数为m，则所有的返回车辆的最小时间间隔为：

将应急物资准备子流程和应急物资调度子流程看成一个整体，称其为“物资准备和调度流程”，则每批物资都要依次经历这个物资准备和调度流程，才能被运送到受灾地。首先计算该流程的总耗时量。其中，政府与供应商对应急物资补充征购谈判的期望耗时量计算如下：设在一轮谈判中，政府与供应商的谈判有失败情况的概率为p(0＜p＜1)，则谈判全部成功的概率为1-p。一旦有失败的情况，政府须重新寻找其他供应商进入下一轮谈判。则这一流程所需时间的期望：

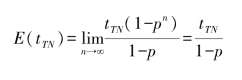
设政府仓库中预先存储的应急物资在得到运输指令后可即刻起运，其准备时间为零。物资准备子过程的耗时量应为“政府直接调运预先准备的库存应急物资”、“政府向供应商补充征购应急物资”(如果需要)、“政府通过媒体请求社会捐赠应急物资”(如果需要)等三个过程的耗时量的最大值。那么这个物资准备和调度流程的总运行时间为：

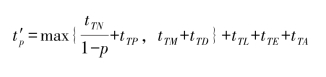
其中，tTN为政府与供应商谈判的耗时量，tTP为谈判成功后供应商准备物资的耗时量，tTM为媒体发出报道所需的时间，tTD为企业从看到媒体报道到准备好捐赠物资的耗时量，tTL为应急物资从供应商启程运往集散地的平均时间，tTE为专家评估各条运输路线的预期通过时间，tTA为计算机利用“重大突发事件应急物资运输调度的模型”运算最优运输路线的耗时量。

根据前面的分析，这个物资准备和调度流程应该在两辆运输车到达物资集散地的最小时间间隔期内完成，故有：

再设在[0，T1]时期内，应急物资的每次需求的发生时间相互独立，且服从负指数分布。在此时期内，共有n次应急物资的需求。那么，可知应急物资需求的平均到达率：

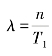(www.xing528.com)

应急物资需求的平均服务率：

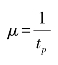
根据排队论的原理，逗留时间服从参数为μ-λ的负指数分布。则逗留时间w的概率密度：

那么平均逗留时间：

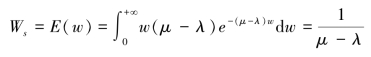
平均等待时间：

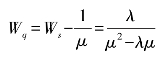
另外，由于灾民的医疗和生活等应急物资必须在一定时间内送达，否则会导致更大的伤亡，所以可设这些应急物资必须在[0，T2]时期内送达。其中，假设物资准备和调度流程中的某个环节i需要n个工作人员共同参与，该环节的耗时量为tpi。则这n个工作人员的总有效工作时间为ntpi。再设这些工作人员的时间利用率为rp(0＜rp＜1)；则该环节所需的工作人员数：

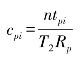
为了提高物资准备和调度流程的运行速度，必须减少某些环节上的排队等待时间。但是，由于各个环节的发生时间一般不相互独立，也不服从一个确定的概率分布，所以用上述传统的排队论模型计算起来就会十分复杂。但是，基于Petri网的工作流系统仿真是解决该问题的有效办法。下面就用该方法来求解每个环节上的排队等待时间等参数。

假设有四批应急物资的请求信息，它们对应的来源方式和准备时间都不相同，以此建立应急物资准备、调度和运输流程的工作流系统，如图5-4所示。系统中每个变迁的含义为：TPi，准备第i批应急物资；TSi，第i次调度；TTi，运输第i批应急物资，其中i＝1，2，3，4。

利用WoPeD软件对图5-4所示的系统进行静态检测，可知该系统通过了可覆盖性(Coverability)，有界性(Boundedness)和活性(Liveness)检验，所以这个系统的设计是合理的。