基于蚁群算法的自学习供应顺序优化方法

因为上节所介绍的应急车辆运输路线的分配方法是以确定的受灾地供应顺序为前提的，所以在使用该方法之前，应该给出受灾地的供应顺序。为了给出尽可能好的顺序，本节将基于蚁群算法设计一个受灾地供应顺序的自学习方法。蚁群算法是一种模拟蚂蚁的群体行为的仿生智能算法，它具有很强的鲁棒性和分布式计算功能，它能够很好地跟其他的算法结合。

蚁群算法最早由意大利学者Dorigo和Maniezzo在1996年提出(Dorigo and Maniezzo，1996)，因为它具有正反馈、分布式计算等特点，所以在求解此类问题的时候，比其他的算法更具优势(丁秋雷等，2007)。Bullnheimer等(1999)首先将蚁群算法的思想应用于车辆路径问题中，但没有从根本上解决搜索速度过慢的问题；Bell等(2004)提出了一种改进蚁群算法，虽然在一定程度上解决了搜索速度问题，但难以求解数据量较大的问题；Reimann等(2004)提出基于节约法的蚁群算法则恰恰相反，虽然能够处理大规模问题，但是搜索速度缓慢。后来，很多关于车辆路径问题的研究都以蚁群算法为基础，旨在解决该算法的早熟问题(Gambardella and Dorigo，2000)。例如Stutzle(2000)提出了最大最小蚁群系统；Gambardella等(2000)提出了混合型蚁群算法HAS。这些算法各有优点与不足，并在解决蚁群算法的过早停滞问题有各自的研究。

在重大突发事件情景下，应急物资运输路径问题与一般情况下的物资运输问题有很大的不同。其特殊性就表现在应急物资需求和车辆数量的不确定性。在突发事件应急物资的运输方面，Yan等(2012)利用蚁群系统和阈值接受技术建立了一个混合算法来解决道路抢修对实际运输造成的障碍问题；Kallioras等(2014)提出了一种一致搜索(IHS)蚁群算法解决了灾后基础设施的管理问题。Korosec等(2013)比较了贪婪搜索，无参数搜索和蚁群共识主动性算法在解决有约束的应急物资运输调度问题中各自的优势和劣势。Hu等(2012)将蚁群算法与微粒群算法结合，研究了地震后紧急避难所的分配问题。

针对应急物资需求量更新的问题，Dan等(2013)将动态的需求过程分割成在时间轴上多个静态的需求，并提出了相应的改进蚁群算法，但其分割的方法难以适用于复杂的动态需求；詹沙磊等(2013)建立了多目标随机规划模型并进行了求解，此模型计算效率较高，但是其假设条件较为苛刻。而马建华等(2011)提出了多车场、多车型最快完成运输的方法，把动态规划和最大流算法引入到模型中，提高了蚁群算法的运行效率和准确度。但是，该方法的实际应用仍受限于很多假设，例如每个受灾点只能由一辆车供给，不考虑车辆返回集散地补给物资重新出发的情况等。

综上所述，虽然目前关于重大突发事件中应急物资的运输调度问题的研究较多，但由于该问题本身非常复杂，所以目前的研究尚没有完全解决这个问题。特别是在算法的适应性和复杂度上面顾此失彼：要么算法理论上可以照顾到很多方面，适应于大多数突发事件，但计算时间过长，无法满足紧急决策的需求；要么算法的计算时间得到了控制，但其前提假设太多，无法适应大多数情况。为了克服这个问题，本章就将把蚁群算法与应急车辆运输路线的分配方法结合，形成一套完整的应急物资运输策略的优化算法。

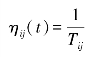
设蚂蚁数量为m，受灾地数量为n。将蚂蚁从i地出发后，紧接着供应j受灾地的决策成为决策对(i，j)。Tij为从i地到j地的最短运输时间。ηij(t)为启发函数，两地之间的最短运输时间越短，启发函数值越大，故有：τij(t)表示t时刻，决策对(i，j)上的信息量。Δτij(t)为一次迭代中，决策对(i，j)的信息增量。表示第k只蚂蚁选择决策对(i，j)后，对此决策对的信息量贡献度。则t时刻，决策对(i，j)的信息量增量为：

设Q为信息强度，Lk表示第k只蚂蚁在本次迭代中所花费的总运输时间。则根据Ant-Cycle模型，有：(www.xing528.com)

为了避免信息量过大，引入信息遗忘因子ρ⊂[0，1)。则在t＋1时刻，决策对(i，j)的信息量为：

再设allowedk为一次迭代中，蚂蚁k在下一步能够选择的受灾地。则在t时刻，蚂蚁k选择决策对(i，j)的概率为：

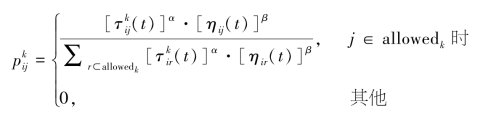
其中，α为信息重要程度因子，β为启发重要程度因子。

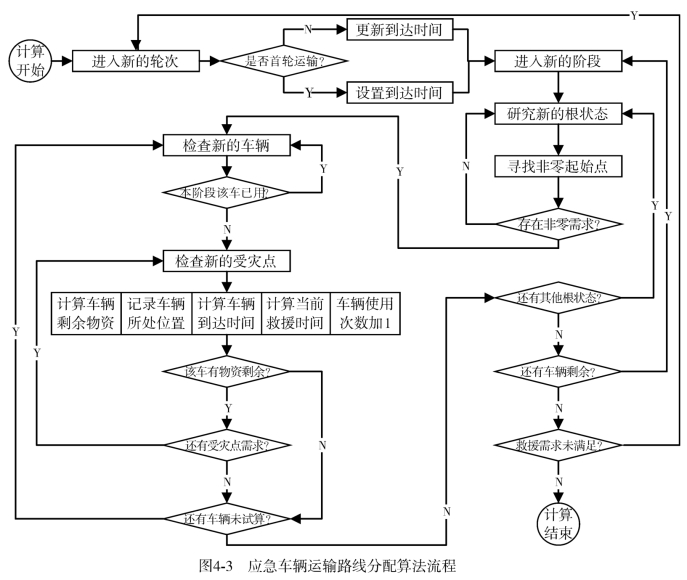
基于上述原理，可以给出受灾地供应顺序算法流程，如图4-4所示。

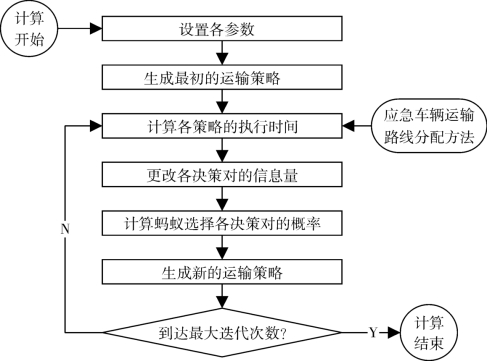
图4-4　受灾地供应顺序算法流程

为了验证上述应急车辆运输路线分配方法和受灾地供应顺序的学习方法的实用性，本章基于Matlab 8.2平台编程实现了这两个算法，并在计算机(CPU：Intel Core i5-3320M，RAM：4GB)上试运行了该程序。从理论上来说，上述算法的迭代次数越多，得到的应急车辆运输路线就应该越接近于最优路线。但在实际的重大突发事件的应急决策中，无法花费太多时间在计算机运算上。但根据反复试验，上述算法迭代50至100次所得到的应急车辆运输路线在大多数情况下很接近最优路线。并且，在受灾地和运输车辆数量各不超过20的情况下，一次迭代耗时量在10秒以内。在这个情况下，计算机的总运行时间约为10分钟，能够满足突发事件情景下的紧急决策对该算法的运算时间的要求。综上所述，本章提出的算法在功能上基本满足了实际问题的需求，在运算速度上也优化得比较好。所以，该算法有实际应用的价值。