基于动态规划的应急车辆运输路线优化方法

上一节中提出的面向需求和车辆数量变更的应急物资运输问题显然是一个NP-Hard问题，直接用智能计算的方法求解是极其繁琐的。事实上，本研究曾尝试直接编程实现蚁群算法对2013年雅安地震中应急物资的最优运输路线进行搜索，结果其计算复杂度太高：在一台现代微型计算机上至少需要4年时间才能算得最终结论。显然，以这种运算速度即使得到了结果，对于应急决策而言，也没有任何意义。因此，本章将该问题的求解分成两个步骤进行：第一步，在给定受灾地的供给顺序的情况下分配运输车辆；第二步，确定受灾地的供应顺序。基于这个思想，第一步就可用动态规划的方法解决，第二步再用蚁群算法来搜索，从而可大幅度减少群算法的搜索范围。

本节研究在给定受灾地的供给顺序的情况下分配运输车辆的方法。具体说来，先给出n个受灾地的供给先后顺序，再将这n个受灾地分配给m个运输车辆，那么车辆i所分配到的x个受灾地必须由该车按照预先给定的供应顺序进行供给。本算法的运行流程如下：

首先，将这个问题依据车辆返回集散地补充物资的次数分成若干个轮次，例如车辆装载应急物资首次从集散地出发为第1轮，车辆第一次返回集散地补充物资后再次出发为第2轮。在同一个轮次中，计算每一辆车供给的具体受灾地，即运输路线。基于此，本问题又被分成若干个阶段，每个阶段只计算一辆车的运输路线。

设车辆k从集散地出发的累计运输次数为dk。再设在某一时刻，受灾地b之前的所有受灾地需求均已经得到满足，车辆k计划从受灾地b开始，依次供给若干个受灾地，直到受灾地p为止。则车辆k花费的运输时间为从集散地到受灾地b的运输时间，加上其所经过的各个受灾地之间的运输时间，即：

此时，车辆k所载的剩余物资量为车辆的载货量减去其所供给的各个受灾地需求量，但当后者大于前者时，车辆k的剩余物资量就为0，即：

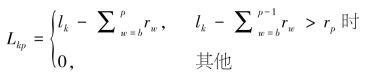
同时，受灾地p的剩余需求为受灾地的需求量减去当前车辆的剩余物资量，但当后者大于前者时，受灾地p的剩余物资量就为0，即：

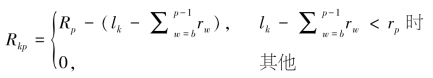
另外，将一个阶段中的m辆车各自的决策看成是一个有m个“根状态”的决策问题，并运用动态规划的思想来解决这个问题。每个根状态都是上一阶段的状态，当前阶段的研究都是基于上一阶段的状态进行的。在受灾地b之前的所有受灾地需求均已经得到满足的情况下，关于第k辆车的状态变量为：

假设该车计划下一步从受灾地b开始依次供给到受灾地p，则其决策变量为：

(www.xing528.com)

状态转移规则为从受灾地b到受灾地p-1，应急物资的需求量均为0，受灾地p的应急物资需求量为Rkp，自身的累计运输次数加1，即：

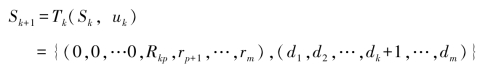
因为一轮运输的总时间是该轮中所有车辆的运输时间的最大值，所以该问题的指标函数为：

在最后一个根状态中，指标函数值为最后一辆车的实际运输时间，即：

而针对一个根状态的最短运输时间，就是求各个指标函数值的最小值，即最优值函数为：

如果在某一轮次中，有车辆k须从外地调到集散地来，则该车辆可参与到本轮的运算中，它到受灾地i的运输时间应为它赶到集散地的时间加上从集散地前往各受灾地的时间，即：

如果当前轮次结束时，仍有受灾地的需求未满足，则须进行下一轮运输。当车辆k在受灾地p时，可认为下一轮中车辆k到受灾地i的运输时间为车辆先从受灾点p返回集散地的时间加上从集散地到受灾地i的运输时间，即：

如果在执行当前策略的过程中，救援信息突然改变，那么m辆车所在的不同地点就可以看成是m个虚拟集散地，每个集散地有且仅有一辆车参加运输，并且车辆离开该虚拟集散地之后，不再返回这里补给物资，而是驶往实际集散地补给。基于此，本书给出应急车辆运输路线分配算法流程，如图4-3所示。