政府单一供应商谈判仿真系统优化建议

前面建立的进化博弈模型给出了供应商和政府双方经过一段时间的学习过程而决定的最终稳定策略。然而，该模型本身难以形象的描绘供应商和政府从最初策略到最终稳定策略之间的决策行为演化过程。而这一过程恰恰是应急物资补充征购谈判和一般物资征购谈判的区别所在。为了有效地研究这一变化过程，本节将引入系统动力学的方法。具体说来，就是将对上述博弈过程中涉及的博弈对象、决策行为和对应价值等因素及其相互关系看成一个系统中的多个组成，然后建立一个反馈动态系统并对其进行仿真分析。

该系统主要由流位变量、流率变量、辅助变量，以及它们之间的相互关系构成。流位变量有两个，分别为供应商选择提供高质量的应急物资的概率(x)，以及政府选择给出高价的概率(y)。流率变量也有两个，分别是上述两个流位变量的变化率(dx/dt和dy/dt)。其余所有变量都是辅助变量，包括：表1中博弈双方的得益(SGH，GHG，SGL，GLG，SPH，GHP，SPL，GLP)；供应商选择提供高质量的应急物资的期望得益(ESG)；供应商选择提供低质量的应急物资的期望得益(ESP)；供应商的平均得益(EDS)；政府选择给出高价的期望得益(EGH)；政府选择给出低价的期望得益(EGL)；政府的平均得益(EDG)；以及模型假设式中所涉及的所有参数。基于此，可通过Vensim软件建立系统流程图，如图3-2所示。

该系统中显示各变量间关系的数学方程设置如下：

"dy/dt"＝EDGT·y

"dx/dt"＝EDST·x

EDGT＝EGH-y·EGH-(1-y)·EGL

EDST＝ESG-x·ESG-(1-x)·ESP

EGH＝GHG·x＋GHP·(1-x)

EGL＝GLG·x＋GLP·(1-x)

ESG＝SGH·y＋SGL·(1-y)

ESP＝SPH·y＋SPL·(1-y)(www.xing528.com)

GHG＝r1·s1-p1-a·b1-u·(1-w1)

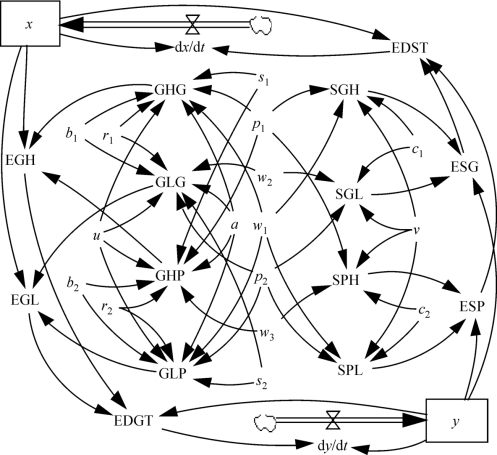
图3-2　应急物资补充征购谈判仿真系统流程图

GHP＝r2·s1-p1-a·b2-u·(1-w3)

GLG＝r1·s2-p2-a·b1-u·(1-w2)

GLP＝r2·s2-p2-a·b2-u·(1-w1)

SGH＝(p1-c1-v)·w1

SGL＝(p2-c1-v)·w2

SPH＝(p1-c2-v)·w3

SPL＝(p2-c2-v)·w1