政府与单一供应商谈判模型的求解优化

由于政府和供应商都不是完全理性的决策者，所以它们在达到最终稳定策略之前往往需要一个学习过程。基于上一部分的假设，本部分运用进化博弈理论对政府和供应商之间针对应急物资补充征购谈判的博弈进行分析。下面依次讨论关于供应商和政府的进化稳定策略。

1.供应商的进化稳定策略

供应商选择提供高质量的应急物资的情况下，其期望得益为：

供应商选择提供低质量的应急物资的情况下，其期望得益为：

从而，供应商的平均得益为：

令为供应商选择提供高质量的应急物资的概率变化率，则根据Weibull提出的进化博弈理论，可得关于x的复制动态方程为：

将(3-1)、(3-2)、(3-3)、(3-4)、(3-9)、(3-10)、(3-11)式代入(3-12)式，整理得到：

博弈达到稳定状态时，x不会随着时间变化而变化，即F(x)＝0。所以，x＝0和x＝1均能达到稳定状态。而对于微小扰动具有稳健性的稳定状态，才是进化稳定策略。基于此，下面再讨论该博弈的进化稳定策略。

则所有的x都是进化稳定策略；

(B)当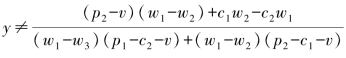时，为使x达到进化稳定策略，由于F(x)连续可导，故其还应满足：

由：

可得到：

所以：

(i)当(p2-v)(w1-w2)＋c1w2-c2w1＜0时，即：

可以得到：

故只有x＝1才能使(3-14)式成立，即x＝1为关于供应商的进化稳定策略。

(ii)当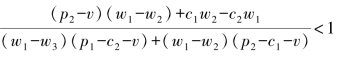，且(p2-v)(w1-w2)＋c1w2-c2w1＞0时，该博弈关于供应商的进化稳定策略为：

此时，由：

得：

又由：

得：

下面证明该式恒成立：

由：

可得：

证毕。

2.政府的进化稳定策略(www.xing528.com)

政府选择给出高价的情况下，其期望得益为：

政府选择给出低价的情况下，其期望得益为：

从而，政府的平均得益为：

令为政府选择给出高价的概率变化率，则关于y的复制动态方程为：

将(3-5)、(3-6)、(3-7)、(3-8)、(3-20)、(3-21)、(3-22)式代入(3-23)式，整理得到：

博弈达到稳定状态时，y不会随着时间变化而变化，即F(y)＝0。所以，y＝0和y＝1均能达到稳定状态。而对于微小扰动具有稳健性的稳定状态，才是进化稳定策略。基于此，下面再讨论博弈的进化稳定策略。

(A)当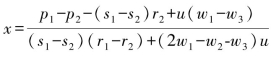时，F(y)≡0，则所有的y都是进化稳定策略；

(B)当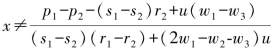时，为使y达到进化稳定策略，由于F(y)连续可导，故其还应满足：

因为：

(i)当p1-p2-(s1-s2)r2＋u(w1-w3)＜0时，即：

可以得到：

故只有y＝1才能使(3-24)式成立，即y＝1为关于政府的进化稳定策略。

(ii)当：

时，即：

此时，该博弈关于政府的进化稳定策略为：

(iii)当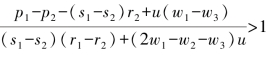时，即：

可以得到：

故只有y＝0才能使(3-24)式成立，即y＝0为关于政府的进化稳定策略。

综上所述，对于政府而言，如果要保证供应商k提供高质量的应急物资，在初始时刻政府和供应商的行动没有倾向性，即x＝0.5；y＝0.5的前提下，根据式(3-16)与(3-17)式，须满足：

或者：

整理可得：

如果政府要保证与供应商k的交易价格为低价，在初始时刻政府和供应商的行动没有倾向性，即x＝0.5；y＝0.5的前提下，根据(3-26)、(3-27)和(3-28)式，必有

或者：

整理可得：

综合(3-29)、(3-30)式，可以得到，政府若要以低价购得高质量的应急物资，则其应该给出的高价和低价分别为：