构建优化模型并求解方法分析

本文构建低碳建筑质量、成本和碳排放多方案目标优选模型的基本思路为，首先确定低碳建筑质量、成本和碳排放的各备选方案，各备选方案应既有区别又有联系，同时体现低碳建筑的特点；然后按照第三章的计算方法针对各备选方案指标进行量化测算，此时可以对不同的备选方案进行初步分析，对比各方案的差异及其产生原因；接下来采用理想点法确定方案的最优解及最劣解；为了保证权重指标的合理性，综合权重采用主观赋权法和客观赋权法相结合的方式进行确定；建立基于TOPSIS法的优选模型，进行贴近度分析并进行排序；最后将数据代入模型，即可进行方案优选。流程如图10-7。

图10-7　多目标方案优选模型构建及求解思路

（1）构造决策矩阵。设决策目标数为n，备选方案为m个，本文中n取值为3；各备选方案的m个决策目标值已获得，记为xij，1≤j≤n，1≤i≤m，用决策矩阵X表示为：

（2）数据标准化处理。本文中质量为效益性指标，成本及碳排放为成本型指标，按照上文所述的数据标准处理公式进行规范后，得到矩阵Y，如下：

（3）确定综合权重。将主观权重αj与熵权法获得的客观权重βj进行合成，过程如下：

（4）加权处理。将指标权重Wj与矩阵Y进行加权合成，然后得到加权处理后的矩阵A如下。

(www.xing528.com)

（5）确定最优解和最劣解。将所有备选方案中各指标存在的最优值，即质量最高、成本最低、碳排放最小的值组成最优解集合Z+；将所有备选方案中各指标存在的最劣值，即质量最低、成本最高、碳排放最大的值组成最优解集合Z-，可表示如下：

其中，

（6）计算各方案到正负理想解的距离。设各方案距离正理想解的n维欧几里得距离值为，各方案距离负理想解的n维欧几里得距离值为，表达式如下：

（7）计算各方案的相对贴近度。

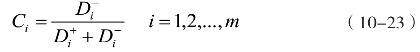
其中，0≤Ci≤1，当相对贴近度的值约接近1，说明该方案越接近最优解且距离最劣解越远；反之则表示该方案距离最劣解近而距离最优解远，应排除。

（8）确定最终方案。将各备选方案计算出的相对贴近度值进行排序，贴近度值最大的为本次多目标方案优选的方案。该最优方案的意义是基于所构建的模型，可使低碳建筑的全寿命周期质量及成本、生命周期碳排放三目标达到综合最优。