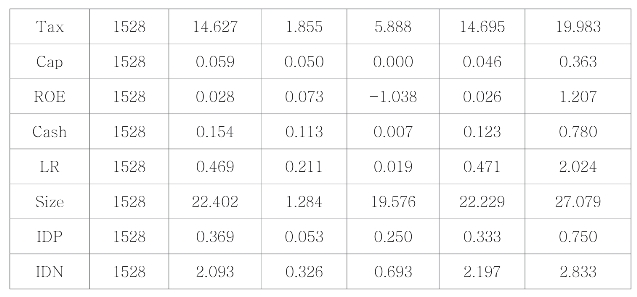
根据表7-1，从A股上市公司提取相应数据进行处理，导入stata软件进行描述性统计。本文对所有变量进行了描述性统计（表7-2）。从描述性统计表2中可以看到，研发投入（RD）取对数之后平均数为17.716，而中位数为17.806，说明更多企业的研发投入金额高于平均水平；对于专利申请数量（PT）的基数来说，其标准差较大，可能为非正态分布，其均值比中位数大，说明多数企业的专利申请数量处于较低水平，且极差的企业专利申请量为0，侧面反映了企业的研发水平不足；环境税（Tax）的最小值为5.888，最大值为19.983，标准差为1.855，说明环境税的企业间环境税的收取有较大的差异；资本支出（Cap）和现金流（Cash）标准差较大，说明企业在这两方面差异较大；企业绩效（ROE）标准差是平均值的两倍多，说明样本极差很大，有些公司处于亏损状态；杠杆率（LR）的最小值为0.019，最大值为2.024，说明个别企业杠杆差异较大，但是均值为 0.469，说明总体的杠杆率适中。独立董事占比（INP）的标准差为0.053，说明企业间独立董事比值差异很小。
表7-2 变量描述性统计
(www.xing528.com)
本文对解释变量与被解释变量进行Pearson相关性分析（表7-3），以初步探究变量之间是否具有相关性。从变量相关系数矩阵表3中，可以初步发现研发投入与环境税的相关系数为0.340，在1%的水平上有显著的正相关关系；专利申请数量与环境税的相关系数为0.134，同样地在1%有显著的正相关关系，这初步说明了环境税的征收是可以促进企业技术创新的，但是需要更准确地检验它们之间的关系还要进行进一步的分析。
表7-3 核心变量的相关系数
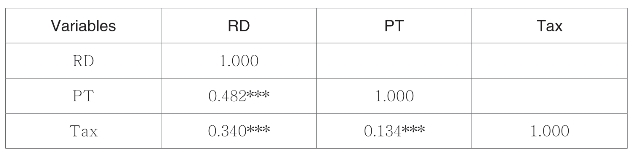
***p〈0.01，**p〈0.05，*p〈0.1
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
