演化稳定策略的分析及优化

（1）企业演化稳定策略分析

令，得x1=0，x2=1，

①若

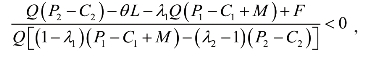
因为λ2-1＜0，故

则进一步可推

即

则

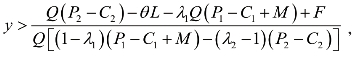
令，可解得x=1。即当

λ1Q（P1-C1+M）-F＞Q（P2-C2）-θL 时，x→1。

②若

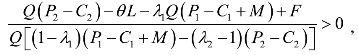
因为λ2-1＜0，故

则进一步可推

即

若

即

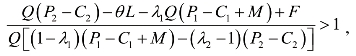
则

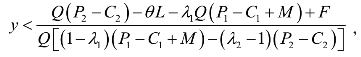
令，可解得x=0。即当

若

此时

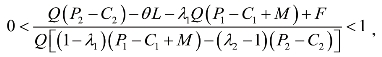
当

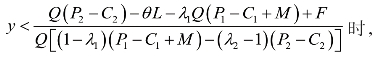
令，可解得x=0；

当

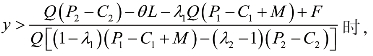
令，可解得x=1。

即当

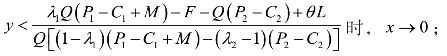
当

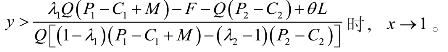
综上所述，得出个条件下的均衡概率趋近表如表4-3。

（2）消费者演化稳定策略分析

令，得y1=0，y2=1，

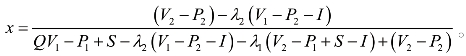
①若

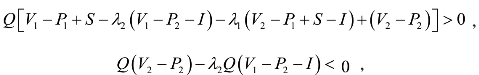
此时

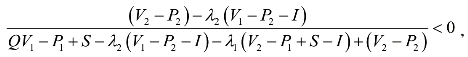
表4-3　均衡概率趋近表

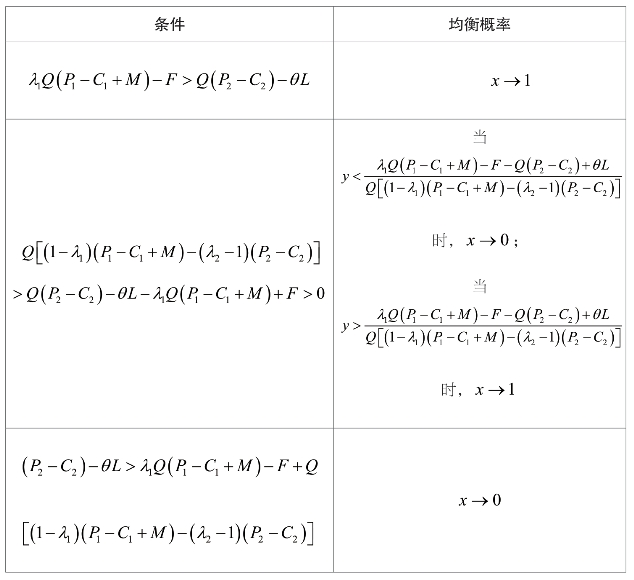
即

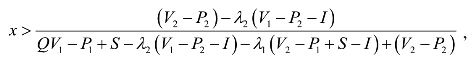
令，可解得y=1。即当

当

②若

此时

当

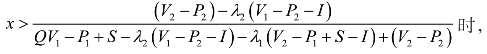
令，可解得y=1。

当

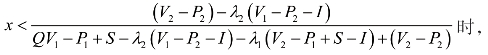
令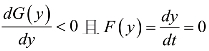，可解得y=0。

即当

当(https://www.xing528.com)

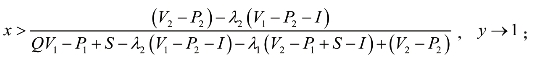
当

③若

此时

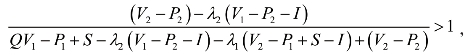
即

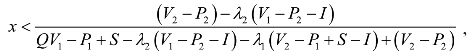
令，可解得y=0。

即当

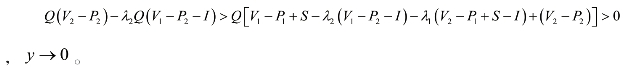
④若

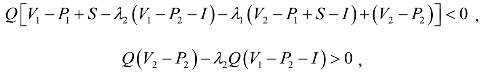
此时

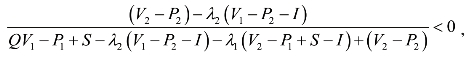
即

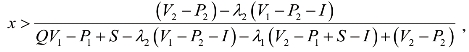
令，可解得y=0，

即当

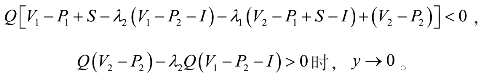
⑤若

此时

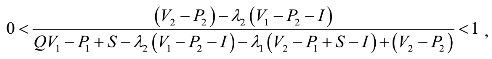
当

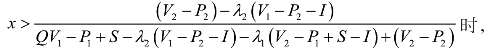
令，可解得y=0。

当

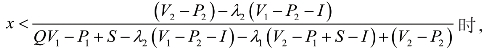
令，可解得y=1。

即当

当

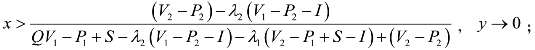
当

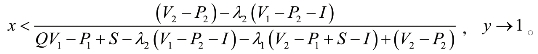
⑥若

此时

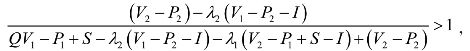
此时

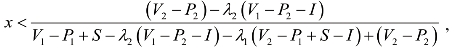
令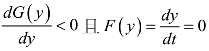，可解得y=1，

即当时，y→1。

综上所述，得出相应条件下的概率趋近表：如表4-4

表4-4　均衡概率趋近表

（3）双方演化稳定策略分析：

由此可得系统的5个可能平衡点：

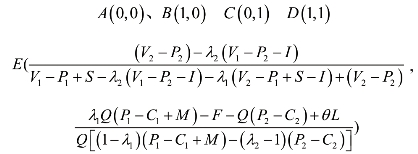
设雅克比矩阵为

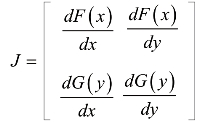
将上述计算结果代入矩阵，得

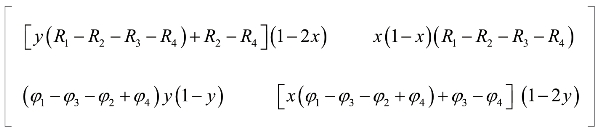
可推出

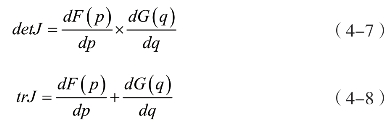
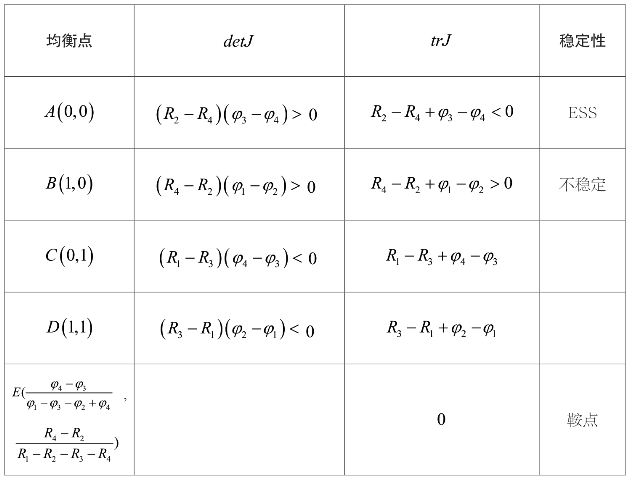
表4-5　双方演化稳定策略均衡点

①当R2＞R4时，即λ1Q（P1-C1+M）-F＞Q（P2-C2）-θL

此时Q（P1-C1+M ）-F＞λ1Q（P1-C1+M）-F、

Q(P2-C2)-θL＞λ2Q(P2-C2)-θL，

故有Q（P1-C1+M）-F＞λ2Q（P2-C2）-θL，即R1＞R3。

表4-6　双方演化稳定策略均衡点（R2＞R4）

②当R2＜R4时，即λ1Q（P1-C1+M）-F＜Q（P2-C2）-θL

I. 当R1＞R3时，即Q（P1-C1+M）-F＞λ2Q（P2-C2）-θL

表4-7　双方演化稳定策略均衡点（R2＜R4）

I. 当R1＜R3时，即Q（P1-C1+M）-F＜λ2Q（P2-C2）-θL

表4-8　双方演化稳定策略均衡点（R1＞R3）