回归分析预测方法是一种重要的市场预测方法,在对企业库存未来的发展状况和水平进行预测时,首先需要了解影响库存需求的主要因素并获得相应的数量资料,在确定自变量和因变量之间相关关系的基础上建立相应变量之间的回归方程,并将回归方程作为预测模型,从而进行相应的预测工作。
(一)一元线性回归模型
在回归分析中,如果变量之间的回归方程为线性方程,则称之为线性回归方程。如果方程中只存在一个自变量和一个因变量,此时将其称为一元线性回归方程。即其数学模型可表示为
![]()
式中,Y为库存需求量;X为影响库存需求的因素;a、b为回归方程中的待定系数。

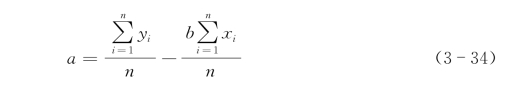
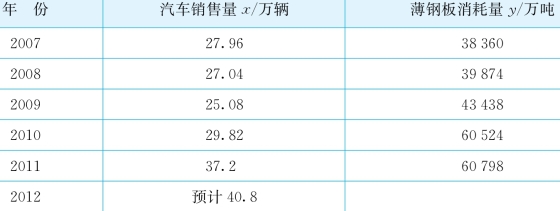
【例3-5】 为了预测某汽车公司薄钢板的年需求量,该公司研究并收集了几年间的汽车产量和薄钢板消耗量的数据,见表3-13。假设预计2012年汽车产量将达到40.8万辆,试用一次性回归预测2012年薄钢板消耗量。
表3-13 该汽车产量与薄钢板消耗量的数据表
解:采用Excel进行回归分析时,单击【数据分析】按钮,在【分析工具】下拉列表框中,选择【回归】选项,单击【确定】按钮,并在【回归】对话框中输入数据区域。表3-14是回归分析的相关输出结果。
表3-14 Excel输出的回归分析结果(https://www.xing528.com)

从回归分析结果看,其包含如下三部分内容。
第一部分为回归分析的常用统计量,包括相关系数(Multiple R)、判定系数r 2、修正后的r 2(Adjusted R Square)、标准误差、观察值的个数。第二部分为方差分析,主要针对回归方程的线性关系进行检验,包括自由度、回归平方和、残差平方和、总平方和(SS)、回归和残差的均方(MS)、检验统计量(F)以及F检验的显著性水平(Significant F)。第三部分为参数估计的相关内容,包括回归方程的截距(Intercept)、斜率(X Variable 1)、截距和斜率的标准差等。由输出结果可得,汽车销售量与薄钢板消耗量之间存在相关关系,其相关方程为y=-4 564.54+1807.05x,当x取40.8时,相应的薄钢板消耗量预测值为69 163.1万吨。
(二)多元线性回归模型
实际库存需求预测过程中,库存需求不仅与单个因素有关,存在着多个因素同时影响需求量的情况。此时就需要运用多元线性回归模型对库存需求进行预测。与一元线性回归模型类似,其回归模型可表示为
![]()
同样,公式3 35中的待定系数可以通过计算机软件获得,在计算回归模型后也需要对其进行相应的数据检验,以判定该回归方程的合理性。
(三)非线性回归模型
无论是一元线性回归还是多元线性回归,利用它们进行计算的前提均为自变量与因变量之间存在线性关系,但实际过程中两者之间的关系往往是非线性的,此时就需要通过散点图分析自变量与因变量之间的相关关系,根据变量间的不同类型为其配合一条与其相适应的回归曲线。最常用的为幂函数形式的方程,该回归模型表示为
![]()
其中,Xn为影响库存需求的因素;a、en为待定系数。解该回归方程时先对方程取对数,将其转换为线性方程进行求解。转换方程为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




