互斥方案的比选及经济效果分析

在项目的工程技术经济分析中，见得较多的是互斥型方案的比选。在方案互斥的条件下，经济效果评价包含两部分内容：一是考查各个方案自身的经济效果，即进行绝对效果检验；二是考查哪个方案较优，即相对效果检验。两种检验缺一不可。

备选方案应满足的条件：

（1）整体功能达到要求。

（2）盈利性达到可接受水平。

（3）范围和时间应一致，效率和费用计算口径应一致。

互斥方案的经济效果评价使用的评价指标可以是价值性指标（如净现值、净年值、费用现值、费用年值），也可以是比率性指标（如内部收益率）。但应注意，采用比率性指标时必须分析不同方案之间的差额（追加）现金流量，否则会导致错误判断。

（一）计算期相同的情况

对于计算期相等的互斥方案，通常将方案的计算期设定为共同的分析期。若采用价值性指标，则选用价值指标最大者为相对最优方案；若采用比率性指标，则需要考查不同方案之间追加投资的经济效益。

1.净现值法

在多个互斥方案中，只有通过绝对效果检验的最优方案才是唯一被接受的方案。对于净现值法而言，可表达为净现值大于或等于零且净现值最大的方案为相对最优方案。

【例8-7】 有A、B两个方案为互斥方案，其计算期内各年的净现金流量见表8-6，用净现值法进行比选（i_c=10%），较优方案是（ ）。

表8-6 互斥方案A、B的净现金流量 （单位：万元）

A.方案A较优

B.方案B较优

C.方案A和B效益一样

D.方案A、B均不能通过绝对检验，没有较优

【解答】

两个方案的净现值分别如下：

NPV_A=-502+100×（P/A，10%，10）=112.46（万元）

NPV_B=-629+150×（P/A，10%，10）=292.69（万元）

由于NPV_A>0，NPV_B>0，故两个方案均通过绝对检验，即它们在经济效果上均是可行的。

由于NPV_B>NPV_A，表明B方案优于A方案。因此，应选择B方案为较优方案。

【答案】 B

2.费用现值法

对于仅有或仅需计算费用现金流量的互斥方案，若各方案的寿命期相同，只需进行相对效果检验，判别准则是：费用现值最小者为相对最优方案。

例如，在水力发电和火力发电之间、在铁路运输和公路运输之间、在水泥结构的桥梁和金属结构的桥梁之间进行选择。这类问题的特点是，无论选择哪一种方案，其效益是相同的，或者是无法用货币衡量的。这时一般只能使用最小费用法。如果上述这类问题中的各方案寿命是相等的，那么就可以用各方案费用的现值进行比较。

【例8-8】 4种具有同样功能的设备，使用寿命均为10年，残值均为0。初始投资和年经营费见表8-7（i_c=10%），则选择（ ）在经济上更为有利。

表8-7 设备投资与费用 （单位：元）

A.设备D B.设备C C.设备B D.设备A

【解答】

由于4种设备功能相同，各方案寿命相等，故可以利用费用现值（PC）选优。4个设备方案的费用现值：

PC_A（10%）=3000+1800×（P/A，10%，10）=14060（元）

PC_B（10%）=3800+1770×（P/A，10%，10）=14676（元）

PC_C（10%）=4500+1470×（P/A，10%，10）=13533（元）

PC_D（10%）=5000+1320×（P/A，10%，10）=13111（元）

其中，设备D的费用现值最小，故选择设备D较为有利。

【答案】 A

3.差额投资内部收益率法

（1）差额投资内部收益率 又称增量投资内部收益率，也称追加投资内部收益率，它是指相比较的两个方案各年净现金流量差额的现值之和等于零时的折现率。其计算公式为

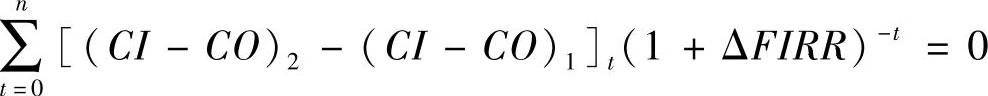
式中 ΔFIRR——差额投资内部收益率；

（CI-CO）₂——投资多的方案的年净现金流量；

（CI-CO）₁——投资少的方案的年净现金流量。

由于差额投资内部收益率的计算式依然是一元n次方程，不易直接求解，故仍然采用与内部收益率相同的求解方法。

（2）差额投资内部收益率的判别准则 首先，前提是每个方案都是可行的，然后将计算求得的差额投资内部收益率ΔFIRR与基准投资收益率i_c（或ΔEIRR与社会折现率i_s）相比较，若ΔFIRR≥i_c时，则投资多的方案为优；若ΔFIRR<i_c，则投资少的方案为优。

多个互斥方案相比选时，先按投资多少由少到多排列，然后，再依次就相邻方案两两比较。被保留方案再与下一个相邻方案比较，计算ΔFIRR，再进行取舍判断。依此不断进行，直至比较完所有方案，最后保留的方案即为相对最优方案。

按内部收益率比选可能与用价值性指标比选的结论不一致，而用差额投资内部收益率比选与用价值性评价指标比选的结论是一致的。

（二）计算期不同的情况

寿命不等的互斥方案的经济效果比选，关键在于使其比较的基础相一致。通常可以采用计算期统一法或年值法进行方案的比选。

1.计算期统一法

计算期统一法就是对计算期不等的比选方案选定一个共同的计算分析期，再进行比选。分析期的设定应根据决策的需要和方案的技术经济特征来决定。通常有以下几种处理方法。

（1）计算期最小公倍数法 此法假定备选方案中有一个或若干个在计算期结束后按原方案重复实施若干次，取各备选方案计算期的最小公倍数作为共同的分析期。

（2）最短计算期法 也称研究期法，此法选择方案中最短的计算期作为各方案的共同计算期。先计算较长计算期方案的项目费用现值或项目净现值，然后折算成年金，再按照已知年金求现值的方法计算出共同计算期年份数的费用现值或净现值进行比较。(www.xing528.com)

【例8-9】 采用机器A和采用机器B的效益相同，采用机器A的初始费用为9000元，在6年使用寿命结束时没有残值，年度运行费5000元。机器B初始费用为16000元，在9年的经济寿命结束时可转卖4000元，年度运行费4000元，折现率为10%。项目应该采用（ ）。

A.机器A、B的费用都太高，不能采用 B.机器A

C.机器B D.机器A、B都可采用

【解答】 因为两个机器的效益相同，所以可以只比较它们的费用，但因为寿命期不同，所以要统一计算期，可采用最小公倍数法或最短计算期法。

（1）最小公倍数法。6和9的最小公倍数为18，则在18年里，A、B方案现金流量图如图8-6所示。

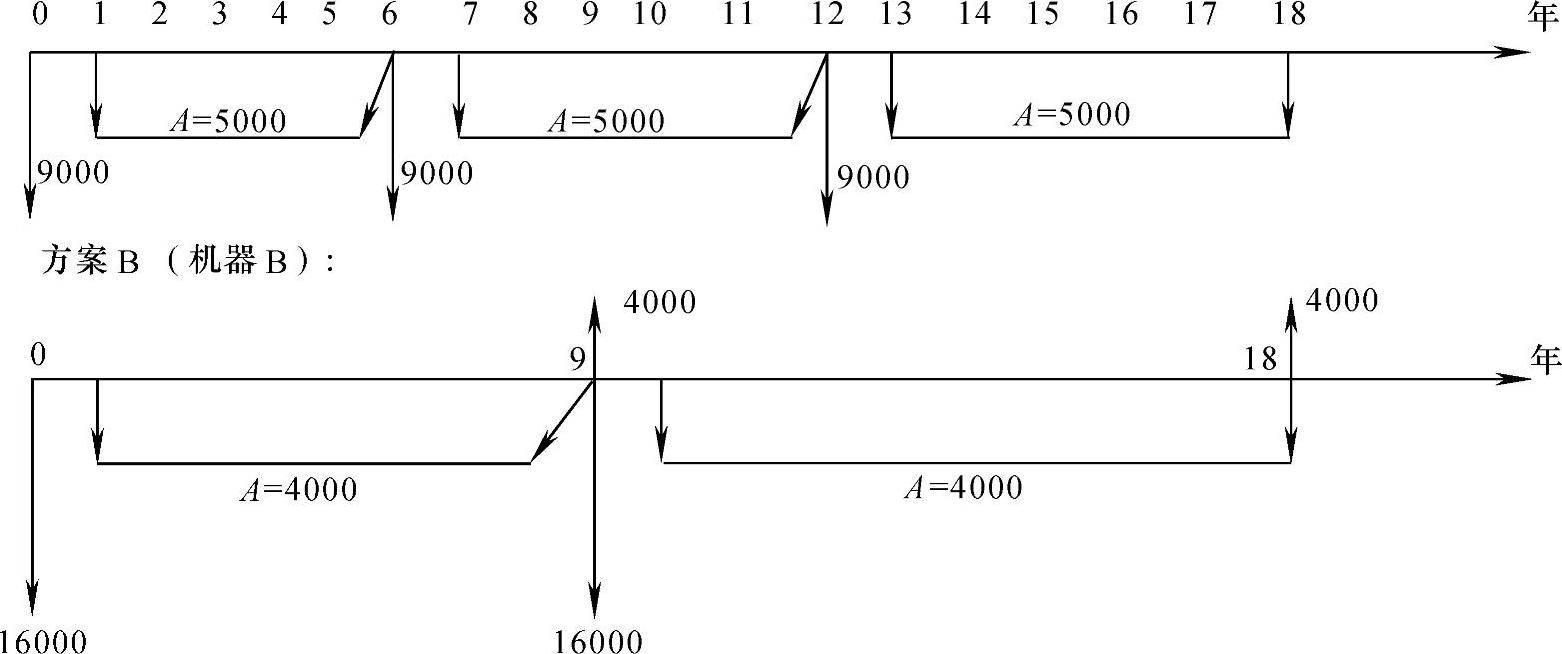
图8-6 A、B方案现金流量图

方案A、B的费用现值分别为PC_A、PC_B：

PC_A=9000+5000（P/A，10%，18）+9000（P/F，10%，6）+9000（P/F，10%，12）

=9000+5000×8.201+9000×0.564+9000×0.319

=57952（元）

PC_B=16000+（16000-4000）（P/F，10%，9）-4000（P/F，10%，18）+4000（P/A，10%，18）

=16000+12000×0.424-4000×0.180+4000×8.201

=53172（元）

可见，PC_B<PC_A，则B方案优于A方案。

（2）最短计算期法，取6年为共同计算期。

A方案6年的费用现值：

PC_A=9000+5000（P/A，10%，6）

=9000+5000×4.355=30775（元）

B方案6年的费用现值：

PC_B=[16000+4000（P/A，10%，9）-4000（P/F，10%，9）]（A/P，10%，9）（P/A，10%，6）

=[16000+4000×5.759-4000×0.424]×0.174×4.355

=28295.13（元）

可见，PC_B<PC_A，则B方案优于A方案。

由此可知用最小公倍数法和最短计算期法的比较结论是一致的。

【答案】 C

2.净年值法

在对计算期不等的互斥方案进行比选时，净年值法是最为简便的方法，当参加比选的方案数目众多时，尤其如此。

（1）计算方法 设m个互斥方案的计算期分别为n₁，n₂，…，n_m（方案j=1，2，3，…，m），在其计算期内的净年值为

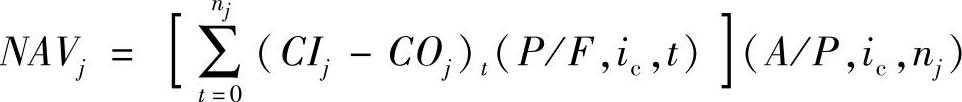
（2）判别准则 净年值大于或等于零且净年值最大的方案为相对最优方案。

（3）前提假定 各备选方案在其寿命结束后均可按原方案重复实施或以与原方案经济效益水平相同的方案持续。

【例8-10】 设互斥方案A、B的计算期分别为5年和3年，各自计算期内的净现金流量见表8-8（i_c=12%），用净年值法评价，较优的方案是（ ）。

表8-8 方案A、B的净现金流量 （单位：万元）

A.方案B较优 B.方案A较优

C.方案A和B效益一样D.方案A、B净现值都小于零，没有较优

【解答】 计算两个方案的净年值：

NAV_A=（-300+80×0.893+88×0.797+96×0.712+106×0.636+121×0.567）（A/P，12%，5）

=46×0.2774=12.76（万元）

NAV_B=（-100+35×0.893+42×0.797+51×0.712）（A/P，12%，3）

=1×0.4163=0.42（万元）

由于NAV_A>NAV_B>0，故选择A方案。

【答案】 B

对于仅有或仅需要计算费用现金流量的互斥方案，比如效益相同又难以计算的方案，可以参照净年值法，用费用年值指标进行比选。判别标准为：费用年值最小的方案为相对最优方案。

（三）互斥型项目方案比选方法小结

最小公倍数法的计算最为简单，但要求重复性假设并事先确定精确的基准收益率；最短计算期法可避免重复性假设；差额投资内部收益率法计算最复杂，但无需事先确定一个精确的折现率。

应当强调指出，选用以上所述各种方法时要特别注意其所做的假设。

最小公倍数法尽管计算简便，但它不适用于技术更新快的产品和设备方案的比较，同样也不适合于处理更新改造项目。

当人们对项目提供的服务或产品有比较明确的期限时，可将此期限作为计算期来进行各方案的比较。

表8-9给出了互斥方案的特点与方法选择。

表8-9 互斥方案的特点与方法选择