常用资金等值换算公式

常用的资金等值换算公式有三对：

（1）现值（P）与终值（F）的相互变换。

（2）年值（A）与终值（F）的相互变换。

（3）年值（A）与现值（P）的相互变换。

（一）现值与终值的相互变换

资金在某一特定时间序列的初始值称为现值（P），在某一特定时间序列的终点值称为终值（F）。用现金流量图表示，如图8-2所示。

注：这里F与P的方向变化只是为了表示的方便，实际并没有发生方向的变化。

1.现值变换为终值（已知P，求F）

现有一项资金P（现值），年利率为i，按复利计算，n年以后的本利和为F，计算公式为

F=P（1+i）ⁿ

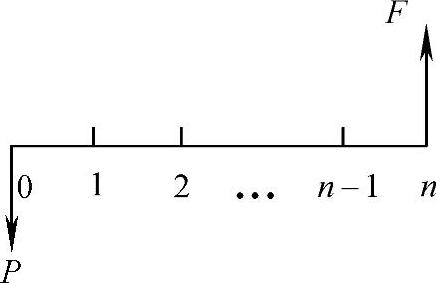
图8-2 P与F的现金 流量图

式中 （1+i）ⁿ——现值P与终值F的等值变换系数，称为整付（或一次支付）本利和系数，又称一次支付终值系数，或简称为终值系数，记为（F/P，i，n）。

斜线右下方表示已知因素，左上方表示未知待求因素。

2.终值变换为现值（已知F，求P）

由F向P的等值变换，公式为

P=F（1+i）^-n

式中 （1+i）^-n——一次支付现值系数，并可记为（P/F，i，n）。

工程经济分析中把由未来值折现到零点，计算现值的过程称为“折现”或“贴现”。

（二）年值与终值的相互变换

年值（A）表示发生在某一特定时间序列各计算期末的等额资金系列的价值。

年值A与终值F的关系用现金流量图表示如图8-3所示。

注：这里F与A的方向变化只是为了表示的方便，实际并没有发生方向的变化。

图8-3 A与F的现金流量图

1.年值变换为终值（已知A，求F）

由等额支付系列现金流量的终值

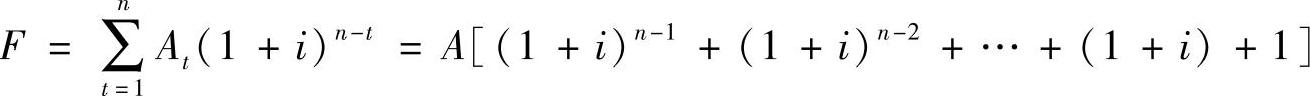
整理得：

式中 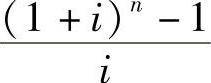——年金终值系数，可记为（F/A，i，n）。

2.终值变换为年值（已知F，求A）(www.xing528.com)

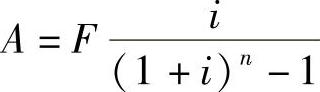
式中 ——偿债基金系数，可记为（A/F，i，n）。

（三）年值与现值的相互变换

年值A与现值P的关系用现金流量图表示如图8-4所示。

注：这里A与P的方向变化只是为了表示的方便，实际并没有发生方向的变化。

1.年值变换为现值（已知A，求P）

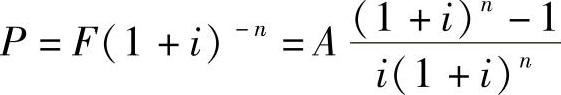
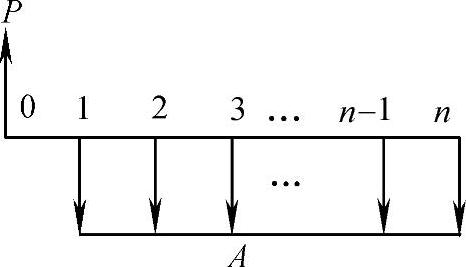
图8-4 A与P的现金流量图

式中 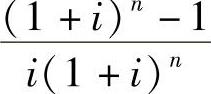——年金现值系数，可记为（P/A，i，n）。

2.现值变换为年值（已知P，求A）

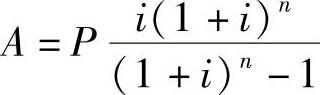
式中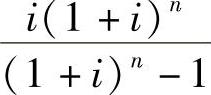——资金回收系数，可记为（A/P，i，n）。当n很大时，资金回收系数约等于i。

（四）资金等值换算小结

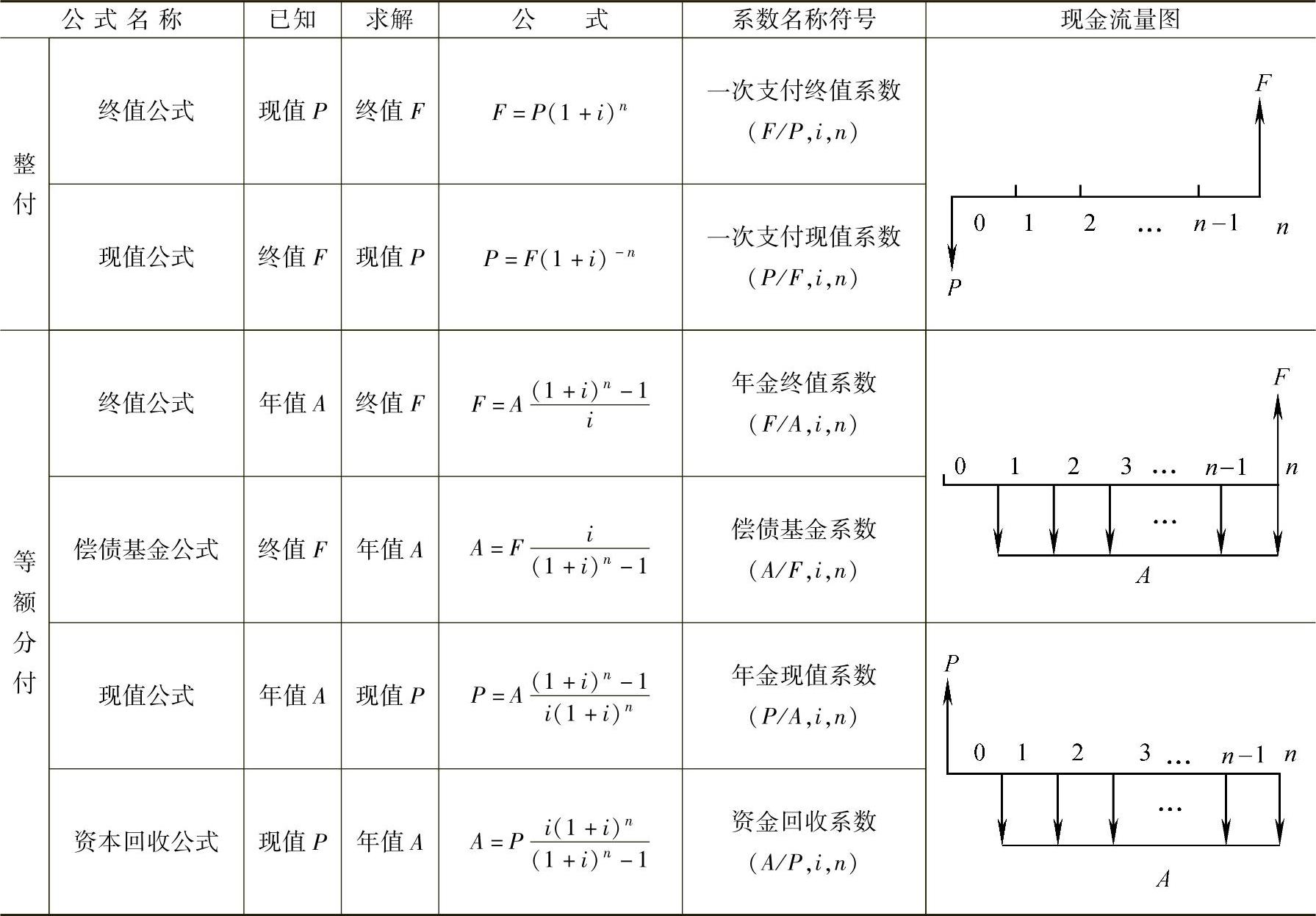
将6个资金等值换算公式以及对应的现金流量图归集于表8-1。

表8-16个常用资金等值换算公式小结

【例8-3】 银行向某企业每年提供500万元的贷款，连续提供10年，每年年初注入，到第十年年末一次还本付息，若年利率为8%，则该企业应偿还的金额为（ ）万元。

A.7243.50 B.6244.00 C.6743.52 D.7822.97

【解答】 现金流量图如图8-5所示。

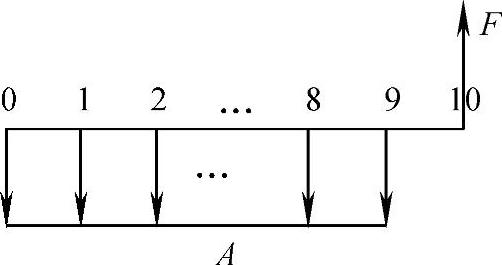
图8-5 现金流量图

根据现金流量图，有：

对于第一年年初的年金在第十年年末的数值为

F=A（1+i）ⁿ=500×（F/A，8%，10）=500×2.1589=1079.45（万元）

对于第一年末到第九年末的年金，根据年金终值系数计算到第九年年末，然后再折算到第十年年末的数值为

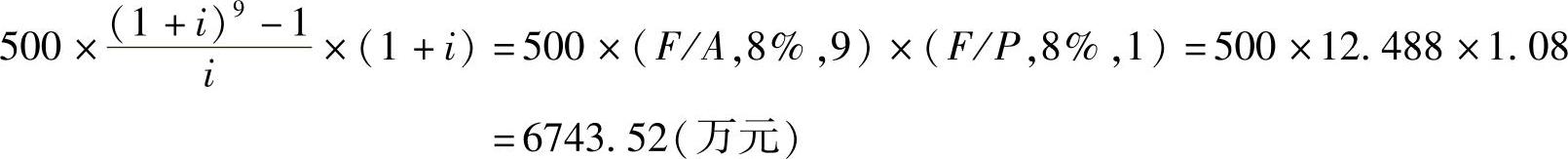
所以第十年末应偿还的资金总额为1079.45+6743.52=7822.97（万元）。

【答案】 D