特殊形式：不变绝对风险厌恶效用函数的应用

前面在效用函数为加性可分的一般情形下，将贸易利益分解为三部分。为了具体求出贸易利益中每一个来源的贡献率，需要给定效用函数的具体形式。假设消费者的子效用函数由不变绝对风险厌恶类型（CARA）代表，即u（i）＝1－e－αq（i）。其中，i为某产品种类；q（i）为消费者对产品种类i的消费量；α为消费者的风险厌恶系数。选择CARA子效用函数的优点在于，在该效用函数假设下，贸易成本的下降会降低企业加成，这种促进竞争效应与诸多经验事实相符。然而，常见的不变替代弹性效用函数（CES）无法体现这一点（Behrens et al.，2014；毛海涛等，2018）。

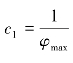假设每个国家的异质性企业生产率均服从帕累托分布，分布函数为或者其中，k为形状参数；为规模参数，即试图进入市场的企业生产率最小值；为企业的边际成本；为企业最小边际成本（即生产率最高的企业的边际成本）；企业生产率的取值区间为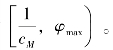当φmax＝∞（或cl＝0）时，进入市场的企业最高生产率为无穷大，意味着企业生产率服从无上界（unbounded）帕累托分布；当φmax＜∞（或c1＞0）时，进入市场的企业最高生产率为有限值，意味着企业生产率服从有上界（bounded）帕累托分布。毫无疑问，后者更符合现实，但是由于前者计算简便，而且有许多良好的性质，所以应用更广泛。本书同时考虑企业生产率服从无上界帕累托分布和有上界帕累托分布两种情形。

假设M（τi）为贸易成本为i∈｛1，2｝时，试图进入国家H的企业数量。当贸易成本为τi，其中i∈｛1，2｝时，国家H消费者效用函数为：

随着贸易成本由τ1下降到τ2，贸易利益为：

其中，ACARA为选择效应，BCARA为促进竞争效应，CCARA为种类效应。它们的具体表达式如下：

（一）企业生产率服从无上界帕累托分布（即cl＝0）

根据毛海涛等（2018）的结论，在无上界帕累托分布假设下，贸易成本的下降并不能影响试图进入市场的企业数量，且对于任意τ，M（τ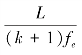）＝恒成立。所以，CCARA＝0，这意味着当生产率服从无上界帕累托分布时，种类效应不存在。这与已有研究结论是一致的（Feenstra，2015，2016）。

进一步，临界边际成本和价格的表达式分别为^[3]：

①可以用Matlab软件的lambertw（·）命令或者Mathematica软件的ProductLog［·］命令求解朗伯W函数。(www.xing528.com)

（二）企业生产率服从有上界帕累托分布（即c1＞0）

在有上界帕累托分布假设下，写出如下形式的自由进入条件，然后求得临界边际成本^[4]。

根据上面的自由进入条件，并不能求出临界边界成本的显性表达式，只能写成如下隐函数形式^[5]。

可以看出，上式左边是一个常数，上式右边在给定τ的前提下，只有一个未知数。为了求得的值，可以通过不断尝试的方法，直到将选取的的值代入等式右边时，与等式左边的误差最小。^[6]

在有上界帕累托分布假设下，由于存在种类效应，还需要计算出M（τ1）和M（τ2）的表达式。在已知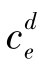（τ）的前提下，根据劳动力市场出清条件，就可以求得M（τ）的表达式。劳动力市场出清条件为：

化简得到^[7]：

观察上式可以发现，在给定的前提下，即可求得Me（τ）的数值。由于基于有上界帕累托分布的分解较为烦琐，而且不是本文的关注重点，本书在后文量化部分并没有基于有上界帕累托分布进行分解，感兴趣的读者可以基于脚注1进行尝试。