封闭市场的均衡条件及影响分析

（一）偏好与需求

将代表性消费者的工资标准化为1，则代表性消费者的效用最大化问题为：

下面构造拉格朗日函数：

其中，Ne为市场均衡条件下，试图进入市场的企业数量；ce为临界边际成本，也就是成功进入市场的企业的边际成本最大值；pe（c）为边际成本为c的企业的价格；qe（c）为代表性消费者对边际成本为c的企业的消费量，而非企业的产出；拉格朗日乘子δa指的是收入的边际效用（marginal utility of incomes），又称影子价格，即消费者多支付一元钱带来的效用增量。

根据消费者效用最大化的一阶条件，代表性消费者的需求函数为：

上面给出的两个需求函数是等价的，通过其中一个式子，可以很容易推导出另一个。在这两个式子中，为所有产品价格之和；用来衡量价格的离散度（price dispersion）^[2]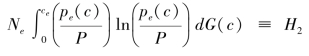；则代表价格分布的微分熵（the differential entropy of the price distribution）^[3]。由于企业数量是一个连续统，企业规模很小，以致于任何一家企业都可以忽略不计。因此，需求函数中的P、H1和H2都是外生给定。

与不变替代弹性需求结构不同，当需求结构为可变替代弹性时，若消费者对某一种类的消费量趋近于零，则边际效用仍然是有界的。因此，存在一个价格的临界值（即保留价格），当一家企业的定价高于这一临界值时，消费者对其消费量降为零。保留价格等于边际成本最高的企业的定价，即同时，对边际成本最高的企业而言，生产与否是没有区别的，因为无论做何选择，利润都等于零。因此，边际成本最高的企业产量为零。

根据消费者从任意两种产品的消费中，获得的边际效用之比等于价格之比。可以得到，消费者从对边际成本最高的企业和其他任意一家企业的消费中，获得的边际效用之比，同样等于他们各自的价格之比。即，

进一步，我们可以基于需求函数，求出边际成本为c的企业的可变需求弹性：

企业在知道自己需求的价格弹性之后，根据边际成本加成定价法，就能确定利润最大化的价格：

所以，边际成本为ce的企业的定价为：

通过式子（5.3）可以看出，边际成本为ce的企业的定价恰好等于该企业的边际成本。

将式子（5.2）和（5.3）代入式子（5.1）得：

由于上式异常复杂，我们并不能直接将qe（c）表示为c的函数，首先将上式变形为：

可以看出，式子（5.4）和Lambert W函数在形式上一致。我们借助Lambert W函数来求解qe（c）。Lambert W函数定义为φ＝W（φ）eW（φ）。因此，令进一步，可以将qe（c）写出W（e的函数。

将式子（5.5）代入式子（5.2），就可以将最优价格写成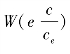的函数。(www.xing528.com)

（二）封闭条件下的零利润条件

根据所有成功进入市场的企业的总利润等于所有试图进入市场的企业的进入成本之和，可以得到第一个均衡条件，即零利润条件：

上式可以化简为：^[4]

将式子（5.8）代入式子（5.7），需要注意的是，积分上限需要变为1，这是因为，当c＝ce时，＝W（e），根据Lambert W函数本身的性质，有W（e）＝1。因此，变换被积函数和积分上限后的积分表达式为：

根据上式，可以求出，在市场均衡条件下，临界边际成本的表达式

其中，积分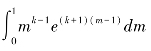的大小由形状参数k唯一决定，给定任意一个k，该积分都有对应的值。

（三）封闭条件下的劳动力市场出清条件

由全社会的劳动力总和等于进入过程和生产过程中所需要的全部劳动力，可以得到第二个均衡条件，即劳动力市场出清条件：

上式可以化简为：^[5]

将式子（5.9）代入上式，可以得到市场均衡条件下，试图进入市场的企业数量Ne的表达式：

（四）封闭条件下，市场均衡的消费者福利

最后，求解代表性消费者的福利。需要注意的是，在产业组织文献中，经常出现寡头厂商净利润大于零的情形，这种情况下，消费者的福利将会大于消费者的效用。这是因为，消费者同时也是企业的所有者，企业利润也会归消费者所有。所以，消费者的福利实际上包括消费者效用和利润分成两部分。但是，在本章框架下，由于假设垄断竞争的市场结构，企业支付进入成本就可以自由进入市场，可以得到，企业总体的净利润为零。因此，消费者的福利等于消费者的效用^[6]。

将式子（5.1），（5.3），（5.6）和（5.8）代入目标函数中福利的表达式得：

化简可得^[7]：