接下来，本书将对企业顾客样本数据进行探索性因子分析（EFA），以检验CB2BE模型中各初级维度界定的有效性，即划分的维度能否与数据相拟合。在进行探索性因子分析之前，首先需要做KMO和巴特莱特（Bartlett）球体检验，进而验证现有量表是否适合做CFA。从最终结果来看，KMO=0.727，并且Bartlett's球形检验显著（p＜0.000），说明该量表适合做CFA，结果详见表5.12。
表5.12 KMO和Bartlett的检验
（资料来源：本书计算得出）
为了防止同源偏差的出现，我们将回收的309份有效问卷中的所有问项同时纳入到探索性因子分析的结构中来，结果显示，问卷中的首因子方差贡献率为11.94%，在可接受范围内。同时，本书采用主成分因子分析法检验量表的效度，以特征根值1为标准来截取数据，并采用方差最大化正交旋转，结果显示，所有问项清晰地载荷为13个因子，累计方差贡献率为79.823%，详细结果参见表5.13。
表5.13 主成分分析结果
续表
(www.xing528.com)
提取方法：主成份分析。
（资料来源：本书计算得出）
总体而言，萃取的因子与本书预设的因子基本吻合，只有“NETI4：Y公司经常和我们讨论合作关系的进展”出现跨因子载荷的情况，并且在两个因子上的载荷都小于0.5，经过分析，该问项确实存在双重语义，故作删除处理。除此以外，各变量相关问题的因子载荷均大于0.5，原有变量信息丢失较少，因子结构比较理想。因此，可以判断问卷存在会聚有效性，详细结果参见表5.14。
表5.14 旋转成份矩阵a
续表
续表
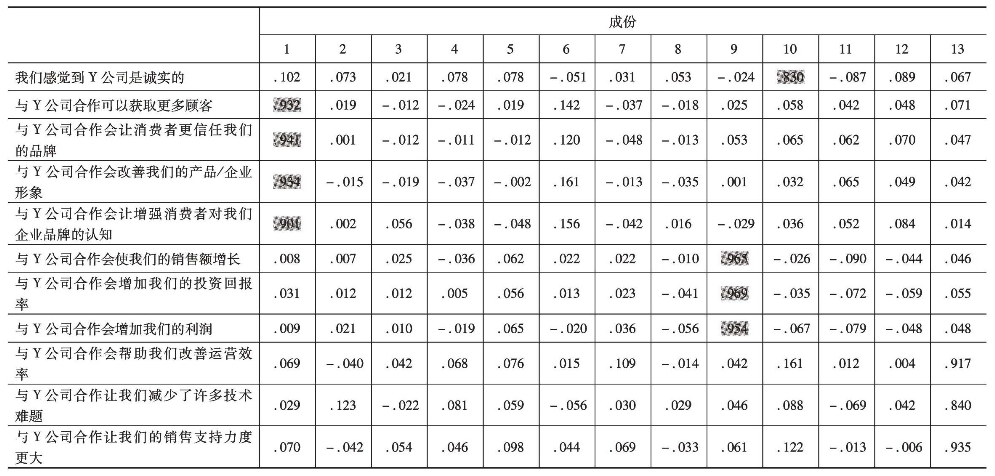
提取方法：主成分分析法。旋转法：具有Kaiser标准化的正交旋转法。
a.旋转在7次迭代后收敛。
（资料来源：本研究计算得出）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
