国际投入产出表与增加值贸易的测算探析

本节对于增加值贸易的计算是建立在约翰逊和诺格拉（Johnson and Noguera，2012）研究基础上的，计算中需借助于国际投入产出表。

第三章第一节中的表3.1和3.2是一个国家的投入产出表，国家投入产出模型是将一国经济作为研究对象的，而世界经济也可以作为相互依赖的诸工艺过程的一个体系来对待（Leontief，1974）。从这个角度来看，国际投入产出模型是国家投入产出模型的思想在区域上的扩展和延伸。随着全球经济一体化的发展，以及国家间依赖程度的加强，国际投入产出模型在区域产业关联、生产模式和生产网络的演进等研究领域逐渐显示出其巨大的应用价值。

国际投入产出表将各国、各行业投入产出关系展示出来，在这样的投入产出框架内，各国各行业使用本国要素——资本、劳动等（也即最初投入）和中间投入进行生产，而中间投入可以来自于国内，也可以来自于其他国家；所有部门的产出均是可贸易的，可以用于最终需求，也可以作为中间投入用于国内或者国外的生产中；最终需求包含消费、投资、政府消费；此外，投入产出表也清晰地描述了各部门产品的流向。

以N个国家、S部门的投入产出表为例（见表4.2），令投入系数

其中，Aij是i国生产的投入到j国的中间投入系数矩阵（i，j=1，…，N，表示国家），是S×S的方阵，其元素Aij（s，t）=Xij （s，t）/Yj（t）（s，t表示行业部门），Xij（s，t）表示i国s部门生产的被j国t部门使用的中间投入品；Yi 、Fi分别表示i国的总产出和最终产品，均为S×1的矩阵。相应的里昂惕夫投入产出均衡方程为：

（4.1）式反映出，全球生产是一个无限循环的过程，并且由无数的生产阶段组成，在每个阶段，对投入的需求等于对产出的使用。

表4.2　国际投入产出表

(www.xing528.com)

注：ROW表示世界其他国家。
资料来源：作者在蒂默（Timmer，2012）三国投入产出表基础上加以扩展。

将总产出和最终使用进行分解：和Fij分别表示i国的总产出和最终产品被j国吸收的部分。则（4.1）式变为从而可以得到分解后的产出矩阵，也即各国产出中被他国（含本国）吸收的矩阵：

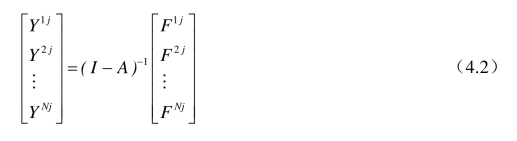
根据Johnson 和Noguera（2012）的界定，增加值出口是指一国创造的，用以满足其他国家最终需求的那一部分增加值。那么i国创造的、被j国吸收的总增加值，也即i国到j国的增加值出口（VAEij）为：

其中，vari 是1×S矩阵，其元素是i国s行业的国内增加值率；Yij是S×1矩阵，其元素表示s行业中i国生产的被j国吸收的产出。从而i国到j国s行业的增加值出口为：

（4.3）和（4.4）式具有如下关系：。通过（4.3）和（4.4）式可以得到双边增加值贸易额，进而可以得到i国的增加值出口总额和增加值进口总额。

本章对中国制造业出口规模与结构以及竞争力等的分析建立在增加值贸易数据的基础上。由于增加值贸易核算方法直接考虑增加值的跨境“流动”和“交易”，剔除了进口中间品的影响，从而能够更准确地反映一国参与全球价值链分工的净贡献以及从分工中的获益。